Элементарные алгоритмические приемы

3.7.1. Последовательное суммирование.

В основе операции последовательного суммирования лежит правило выполнения операции присваивания, согласно которому при выполнении на ЭВМ выражения

S = S + A (1)

сначала вычисляется выражение записанное в правой части, а затем полученное значение заносится в ячейку памяти, отведенную для хранения переменной, записанной в левой части выражения (1). Поэтому если до выполнения выражения (1) имели S = 6; a = 8, то после выполнения выражения (1) переменная S будет иметь значение 14.

Использование операции (1) позволяет построить эффективные алгоритмы в виде циклического процесса при решении многих задач:

- вычисление сумм рядов;

- суммировании элементов массивов;

- численном расчете интегралов и т. п.

Рис.3.8.8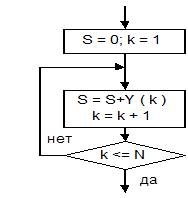

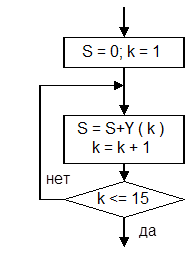
Пример. Составить алгоритм вычисления суммы 15 элементов массива У. В данном случае заранее известно сколько циклов надо выполнять, поэтому можно использовать любую модификацию цикла, в том числе и цикл с постусловием. Очевидно, что для применения формулы (1) до начала цикла надо задать начальное значение переменной S. Обычно начальное значение S задают равным нулю или первому значению из набора суммируемых переменных. Фрагмент алгоритма решения задачи подобным образом приведен на рис.3.8.8.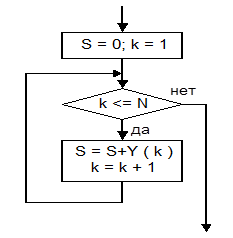

Более общей является задача, в которой необходимо суммировать различное число элементов массива, задаваемое, например, переменной N. Так как в общем случае N может быть равно нулю, алгоритм подобный приведенному на рис.3.8.8 может давать неправильный результат при N = 0. Поэтому для решения подобной задачи следует использовать цикл с предусловием и задавать начальное значение переменной S равным нулю как показано на рис.3.8.9.

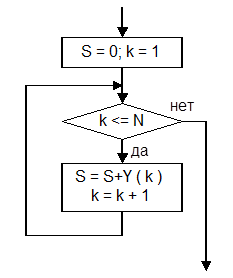
Рис.3.8.9.

3.7.2. Последовательное умножение.

В основе операции последовательного умножения лежит выражение вида

Р = Р * В (2)

То есть после умножения переменной Р на некоторое значение В результат заносится в ячейку памяти, отведенную для хранения переменной Р. Например, если было Р = 5 и В = 3, то после выполнения выражения (2) получим Р = 15.

Использование выражения (2) в циклическом процессе позволяет построить эффективные алгоритмы возведения переменной в степень, вычисления факториала, возведения (- 1) в степень, вычисления произведений, вычисления полиномов и т.п.

Очевидно, что до цикла должно быть определено начальное значение умножаемой переменной (Р), причем оно не должно быть равно нулю.

Пример: вычисление R = X ^N. Так как в общем случае N может быть равно нулю, необходимо использовать цикл с предусловием и задать начальное значение переменной R равным единице. Фрагмент алгоритма решения этой задачи приведен на рис.3.8.10.

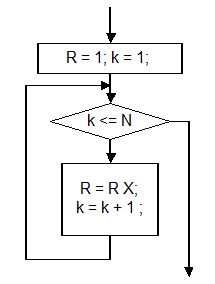
Рис.3.8.10.

Заметим, что для вычисления (- 1) ^N * X ^N достаточно в алгоритме рис. 3.8.10 заменить

R = R * X на R = - R * X.

3.7.4. Перестановка данных.

Существует много задач, в которых необходимо менять местами значения переменных:

- упорядочение элементов массива в возрастающем или убывающем порядке;

- перестановка строк или столбцов двумерного массива по определенному правилу (при решении систем уравнений) и т.п.

Любую перестановку значений осуществляют через вспомогательную переменную, которую используют для временного запоминания одного из переставляемых значений. Например, для перестановки значений переменных А и В достаточно выполнить следующие операции:

Р = А; А = В; В = Р.

Перестановку значений элементов массива также осуществляют через простую переменную. Например, после выполнения фрагмента

Т = У(К); У(К) = У(М); У(М) = Т

значения элементов У(К) и У(М) поменяются местами.

Дата добавления: 2014-01-03