При получении оценочного интервала для какой-либо величины брать среднее значение, либо проводить вычисление до конца, получая максимум и минимум всего выражения

2) При наличии неизвестных величин типа p(C|`AÇ`B) или p(C|~(AÇB)) считать их равными 0 или 1 из логических соображений.

3.2.5.3. Приближенные вероятностные рассуждения

Рассмотрим схему приближенного рассуждения, использованную в ЭС MYCIN и EMYCIN.

В этой схеме вместо вероятности использованы так называемые коэффициенты определенности. Если есть посылка A, импликация AèB и заключение B, то коэффициент определенности посылки ct(A) эквивалентен вероятности посылки p(A), коэффициент определенности импликации ct(AèB) эквивалентен условной вероятности заключения при истинности посылки p(B|A), а коэффициент определенности заключения находится следующим образом:

ct(B) = ct(A)·ct(AèB)

Конъюнктивная посылка

Для конъюнкции посылок:

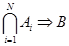
Коэффициент определенности конъюнкции посылок равен коэффициенту определенности наименее надежной из посылок:

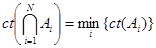
Если сравнить с формулой для точных вероятностных рассуждений, то оценку можно назвать оптимистической

Дизъюнктивная посылка

Для дизъюнкции посылок:

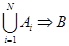
Коэффициент определенности дизъюнкции посылок равен коэффициенту определенности наиболее надежной из посылок:

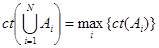
Если сравнить с формулой для точных вероятностных рассуждений, то оценку можно назвать пессимистической

Как правило, посылки не формулируют в виде дизъюнкций. Импликацию с дизъюнкцией в посылке можно разбить на совокупность отдельных импликаций с указанием вероятностей для каждой посылки и импликации:

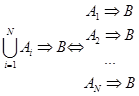
Решение о той или иной формулировке принимается экспертом в соответствии с его представлениями о данном правиле.

Поддержка одного заключения множеством правил

Если есть множество независимых правил с одним заключением:

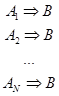
то коэффициент определенности заключения ct_i(B) для каждого из этих правил находится независимо. Рассмотрим, как рассчитать единый коэффициент определенности заключения.

Для случая двух правил ct(B) = ct₁(B) + ct₂(B) - ct₁(B)*ct₂(B). Это выражение удачно иллюстрируется кругами Эйлера.

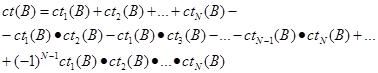
Это правило есть прямая аналогия правила И/ИЛИ.

Биполярные коэффициенты уверенности

В системе EMYCIN используется схема коэффициентов определенности с одним дополнением, а именно - с биполярностью. +1 обозначает полную уверенность, -1 - полную неверность заключения или посылки, 0 - отсутствие информации. Определенный положительный момент этой схемы состоит в том, что коэффициент определенности отрицания утверждения противоположен коэффициенту определенности утверждения. В этом случае вышеприведенные формулы преобразятся следующим образом:

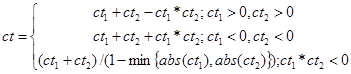
Недостатком схемы можно назвать тот факт, что коэффициенты определенности для большего числа посылок должны вычисляться рекуррентно через формулу для двух посылок.

Дата добавления: 2014-01-03