ЛЕКЦИЯ № 2. Алгоритмы циклической структуры

Цель лекции: Приобретение навыков построения алгоритмов циклической структуры.

Базовая структура цикл. Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла. Используется при решении задач табулирования и построения графиков функций, вычисления сумм и произведений (конечных и бесконечных), решения уравнений и т.п. Алгоритмы, реализующие такие вычисления, называют циклическими, а повторяющиеся участки вычислений - циклами. Использование циклов позволяет выполнять большие объемы вычислений при помощи компактных программ. Структура цикл существует в трех вариантах: цикл с предусловием (цикл ПОКА), цикл с постусловием (цикл ДО) и цикл с параметром. На рисунке 10 изображен цикл с предусловием, а на рисунке 11 – цикл с постусловием, которые называют условными циклическими алгоритмами

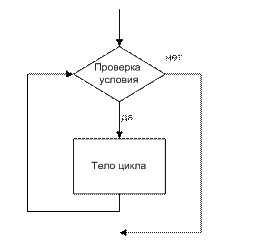. Рисунок 2.1-Цикл--ПОКА

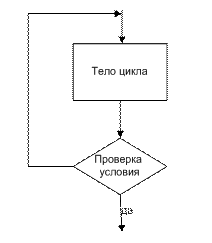Рисунок 2.2- Цикл-ДО

Эти циклы взаимозаменяемы и обладают некоторыми отличиями.

· в цикле с предусловием условие проверяется до тела цикла, в цикле с постусловием – после тела цикла;

· в цикле с постусловием тело цикла выполняется хотя бы один раз, в цикле с предусловием тело цикла может не выполниться ни разу;

· в цикле с предусловием проверяется условие продолжения цикла, в цикле с постусловием – условие выхода из цикла.

При написании условных циклических алгоритмов следует помнить следующее. Во-первых, чтобы цикл имел шанс когда-нибудь закончиться, содержимое его тела должно обязательно влиять на условие цикла. Во-вторых, условие должно состоять из корректных выражений и значений, определенных еще до первого выполнения тела цикла.

Кроме того, существует безусловный циклический алгоритм (рисунок 2.3), который удобно использовать, если известно, сколько раз необходимо выполнить тело цикла.

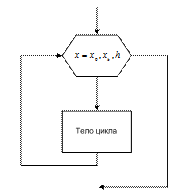Рисунок 2.3- Цикл с параметром

Типичным примером такого алгоритма является алгоритм решения задачи табулирования функции одной переменной.

Пример. Вычислить значения функции у = f(x) некоторой переменной х, изменяющейся от начального значения х_о до конечного x_k с постоянным шагом h. Эта задача реализуется с помощью цикла с заданным количеством повторений, которое определяется как n =mod((x_k-x_o)/h)+1. Процедура вычислений сводится к следующему: вычисляется значение у для начального значения x, равного x₀. Затем х увеличивается на значение шага h, и для него вычисляется значение у. Последний этап повторяется до тех пор, пока х не превысит конечного значения x_k. (Схема алгоритма решения задачи приведена на рисунке 2.4). Переменная х называется параметром цикла. Назначение блоков 1, 2 и 8 ясно из схемы алгоритма. В блоке 3 осуществляется подготовка цикла -присвоение начального значения х_о параметру цикла х. Блоки 4 и 5 представляют собой тело цикла, т. е. участок вычислений, повторяющихся при различных значениях параметра цикла. В блоке 6 текущее значение параметра цикла x увеличивается на значение шага h. Результат операции х+h присваивается переменной x, предыдущее значение х при этом стирается. В блоке 7 проверяется условие продолжения цикла. При выполнении условия х<=x_k цикл повторяется, при невыполнении — повторение цикла прекращается, т. е. осуществляется выход из цикла.

Рисунок 2.4- Цикл с заданным числом повторений с использованием блока условия

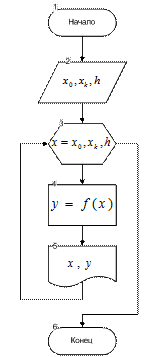Рисунок 2.5- Цикл с заданным числом повторений с использованием блока модификации

C использованием блока модификации схема алгоритма имеет вид, приведенный на рисунке 2.5. Блок модификации 3 помещается в начале цикла и выполняет те же функции, что и блоки 3, 6, 7 в схеме на рисунке 2.4. Запись х = x_о, x_k, h, помещенная в блоке модификации, представляет собой заголовок цикла и предписывает следующие действия: «Для x, изменяющегося от x₀ до x_k с шагом h, выполнить операции, указанные в блоках, следующих за блоком модификации, и ограниченные линией, входящей слева в блок модификации». Выход из цикла обозначается линией связи, выходящей справа из блока модификации. Если величины x₀, x_k, h представлены в блоке модификации константами, например x = 0,50,1, то при значении шага, равном единице, его запись можно опустить: х=0, 50

Оформление схем циклических алгоритмов с использованием блока модификации является предпочтительным.

Рассмотрим использование алгоритмов циклической структуры на конкретных примерах.

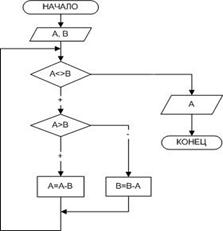Пример 1. Найти наибольший общий делитель (НОД) двух натуральных чисел А и В. Входные данные: А и В. Выходные данные: А – НОД.

Для решения поставленной задачи воспользуемся алгоритмом Евклида: будем уменьшать каждый раз большее из чисел на величину меньшего до тех пор, пока оба значения не станут равными.

В блок–схеме решения задачи, представленной на рис. 2.6, для решения поставленной задачи используется цикл с предусловием, то есть тело цикла повторяется до тех пор, пока А не равно В.

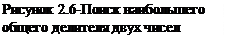Пример 2. Вводится последовательность чисел, 0 – конец последовательности. Определить, содержит ли последовательность хотя бы два равных соседних числа.

Входные данные: X₀ – текущий член последовательности, X₁ – следующий член последовательности.

Выходные данные: сообщение о наличии в последовательности двух равных соседних элементов.

Вспомогательные переменные: F_l – логическая переменная, сохраняет значение «истина», если в последовательности есть равные рядом стоящие члены и «ложь» - иначе.

Блок–схема решения задачи приведена на рисунке. 2.7. Применение здесь цикла с постусловием обосновано тем, что необходимо вначале сравнить два элемента последовательности, а затем принять решение об окончании цикла.

Пример 3. Вычислить факториал числа N (N!=1*2*3 …*N).

Входные данные: N– целое число, факториал которого необходимо вычислить.

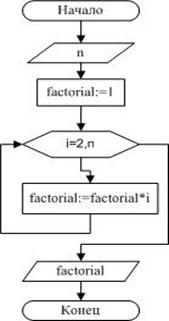Выходные данные: factorial– значение факториала числа N, произведение чисел от 1 до N, целое число.

Промежуточные данные: i– целочисленная переменная, принимающая значения от 2 до N с шагом 1, параметр цикла. Блок-схема приведена на рисунке 2.8.

Итак, вводится число N. Переменной factorial, предназначенной для хранения значения произведения последовательности чисел, присваивается начальное значение, равное единице. Затем организуется цикл, параметром которого выступает переменная i. Если значение параметра цикла меньше или равно N, то выполняется оператор тела цикла, в котором из участка памяти с именем factorial считывается предыдущее значение произведения, умножается на текущее значение параметра цикла, а результат снова помещается участок памяти с именем factorial. Когда параметр i становится больше N, цикл заканчивается, и на печать выводится значение переменой factorial, которая была вычислена в теле цикла.

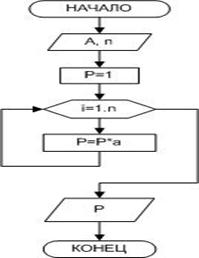Пример 4. Вычислить aⁿ(n>0).

Входные данные: a – вещественное число, которое необходимо возвести в целую положительную степень n.

Выходные данные: p (вещественное число) – результат возведения вещественного числа a в целую положительную степень n.

Промежуточные данные: i– целочисленная переменная, принимающая значения от 1 до n с шагом 1, параметр цикла. Известно, что для того, чтобы получить целую степень n числа a, нужно умножить его само на себя n раз. Результат этого умножения будет храниться в участке памяти с именем p. При выполнении очередного цикла из этого участка предыдущее значение будет считываться, умножаться на основание степени a и снова записываться в участок памяти p. Цикл выполняется n раз.

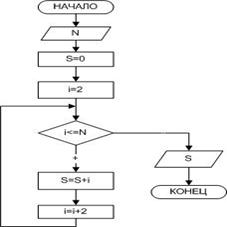
Пример 5. Вычислить сумму натуральных четных чисел, не превышающих N.

Входные данные: N – целое число.

Выходные данные: S – сумма четных чисел.

Промежуточные данные: i – переменная, принимающая значения от 2 до N с шагом 2, следовательно, также имеет целочисленное значение.

При сложении нескольких чисел необходимо накапливать результат в определенном участке памяти, каждый раз считывая из этого участка предыдущее значение суммы и прибавляя к нему следующее слагаемое. Для выполнения первого оператора накапливания суммы из участка памяти необходимо взять такое число, которое не влияло бы на результат сложения. Т.е. перед началом цикла переменной, предназначенной для накапливания суммы, необходимо присвоить значение нуль.

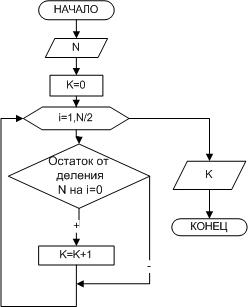Пример 6. Дано натуральное число N. Определить К – количество делителей

этого числа, не превышающих его (N=12, его делители 1, 2, 3, 4, 6, K=5).

Входные данные: N – целое число.

Выходные данные: целое число K – количество делителей N.

Промежуточные данные: i – параметр цикла, возможные делители числа N.

В блок-схеме, изображенной на рисунке 2.11, реализован следующий алгоритм: в переменную K, предназначенную для подсчета количества делителей заданного числа, помещается значение, которое не влияло бы на результат, т.е. нуль. Далее организовывается цикл, в котором изменяющийся параметр i выполняет роль возможных делителей числа N. Если заданное число делится нацело на параметр цикла, это означает, что i является делителем N, и значение переменной K следует увеличить на единицу. Цикл необходимо повторить N/2 раз.

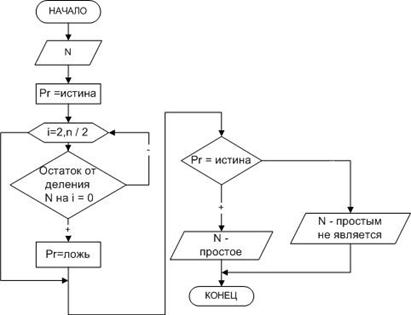Пример 7. Дано натуральное число N. Определить, является ли оно простым. Натуральное число N называется простым, если оно делится нацело без остатка только на единицу и N. Число 13 – простое, так как делится только на 1 и 13, N=12 не является простым, так как делится на 1, 2, 3, 4, 6 и 12.

Входные данные: N – целое число. Выходные данные: сообщение.

Промежуточные данные: i – параметр цикла, возможные делители числа N.

Алгоритм решения этой задачи (рисунок 2.12) заключается в том, что число N делится на параметр цикла i, изменяющийся в диапазоне от 2 до N/2. Если среди значений параметра не найдется ни одного числа, делящего заданное число нацело, то N – простое число, иначе оно таковым не является. Обратите внимание на то, что в алгоритме предусмотрено два выхода из цикла. Первый естественный, при исчерпании всех значений параметра, а второй - досрочный. Нет смысла продолжать цикл, если будет найден хотя бы один делитель из указанной области изменения параметра.

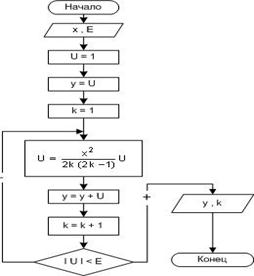Пример 8. Вычислить значения функции 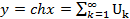используя рекуррентную 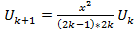(k=1,2,3,…) формулу. Вычисления прекратить при выполнении условия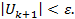

Определить количество итераций. Начальные значения параметров равны U₁=1; x=5.5; точность ε принять равной 10^-4.

Входные данные: U – начальное приближение, х, E – точность (ε).

Выходные данные: y — значение вычисленной функции, k — количество итераций.

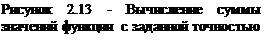
Пример 9. Дано натуральное число N. Определить самую большую цифру и ее позицию в числе (N=573863, наибольшей является цифра 8, ее позиция – четвертая слева).

Входные данные: N – целое число.

Выходные данные: max – значение наибольшей цифры в числе, pos – позиция этой цифры в числе.

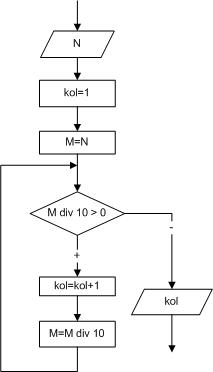Промежуточные данные: i – параметр цикла, kol – количество цифр в числе, M – переменная для временного хранения значения N.

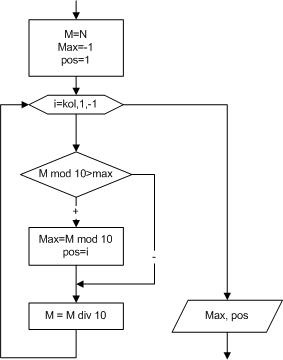Разобьем решение этой задачи на два этапа. Вначале найдем количество цифр в заданном числе (рисунок 2.14), а затем определим наибольшую цифру и ее позицию (рисунок 2.15). Для того, чтобы подсчитать количество цифр в числе, необходимо определить, сколько раз заданное число можно разделить на десять нацело. Если цифры числа известны, определить наибольшую из них не составит труда. Алгоритм поиска максимального значения в некоторой последовательности цифр заключается в следующем. В ячейку, в которой будет храниться максимальный элемент (max), записывают значение, меньшее любого из элементов последовательности (в нашем случае max=-1, так как цифры числа находятся в диапазоне от 0 до 9). Затем сравнивают элементы последовательности со значением ячейки max, если найдется элемент, превышающий значение предполагаемого максимума, то ячейке max необходимо присвоить значение этого элемента и, соответственно, запомнить его номер в последовательности (в нашем случае переменной pos присваивается значение параметра цикла i).

В алгоритме поиска минимума вначале в переменную min записываем значение, заранее большее любого элемента последовательности. Затем все элементы последовательности сравниваем с min, если встретится значение меньшее, чем min, переписываем его в переменную min

Задания по циклическим алгоритмам

Вариант 1

1. Hе используя стандаpтные функции (за исключением abs), вычислить сумму следующего pяда с заданной точностью Е>0 (Е вводится с клавиатуры):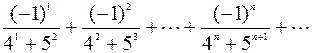

2. Даны целые числа K и N (N > 0). Вывести N раз число K.

3. Даны положительные числа A и B (A > B). На отрезке длины A размещено максимально возможное количество отрезков длины B (без наложений). Не используя операции умножения и деления, найти длину незанятой части отрезка A.

Вариант 2

1. Hе используя стандаpтные функции, вычислить сумму n первых членов следующего pяда (n вводится с клавиатуры): .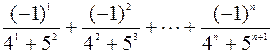

2. Даны два целых числа A и B (A < B). Вывести в порядке возрастания все целые числа, расположенные между A и B (включая сами числа A и B), а также количество N этих чисел.

3. Даны положительные числа A и B (A > B). На отрезке длины A размещено максимально возможное количество отрезков длины B (без наложений). Не используя операции умножения и деления, найти количество отрезков B, размещенных на отрезке A.

Вариант 3

1 Дано действительное число х. Hе используя стандаpтные функции (за исключением abs),вычислить сумму следующего pяда с заданной точностью Е>0 (Е, x вводятся с клавиатуры): .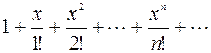

2. Даны два целых числа A и B (A < B). Вывести в порядке убывания все целые числа, расположенные между A и B (не включая числа A и B), а также количество N этих чисел.

3. Даны целые положительные числа N и K. Используя только операции сложения и вычитания, найти частное от деления нацело N на K, а также остаток от этого деления.

Вариант 4

1. Дано действительное число х. Hе используя стандаpтные функции, вычислить сумму n первых членов следующего pяда (n, х вводятся с клавиатуры): .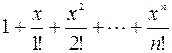

2. Дано вещественное число — цена 1 кг конфет. Вывести стоимость 1, 2, …, 10 кг конфет.

3. Дано целое число N (> 0). Если оно является степенью числа 3, то вывести True, если не является — вывести False.

Вариант 5

1 Дано действительное число х. Hе используя стандаpтные функции (за исключением abs), вычислить сумму следующего pяда с заданной точностью Е>0 (Е, x вводятся с клавиатуры): .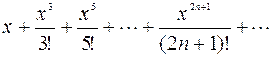

2. Дано вещественное число — цена 1 кг конфет. Вывести стоимость 0.1, 0.2, …, 1 кг конфет.

3. Дано целое число N (> 0), являющееся некоторой степенью числа 2: N = 2 ^K. Найти целое число K — показатель этой степени.

Вариант 6

1. Дано действительное число х. Hе используя стандаpтные функции, вычислить сумму n первых членов следующего pяда (n, х вводятся с клавиатуры): .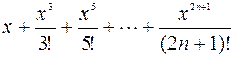

2. Дано вещественное число — цена 1 кг конфет. Вывести стоимость 1.2, 1.4, …, 2 кг конфет.

3. Дано целое число N (> 0). Найти наименьшее целое положительное число K, квадрат которого превосходит N: K ² > N. Функцию извлечения квадратного корня не использовать.

Вариант 7

1 Дано действительное число х. Hе используя стандаpтные функции (за исключением abs), вычислить сумму следующего pяда с заданной точностью Е>0 (Е, x вводятся с клавиатуры): .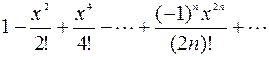

.2. Даны два целых числа A и B (A < B). Найти сумму всех целых чисел от A до B включительно.

3. Дано целое число N (> 0). Найти наибольшее целое число K, квадрат которого не превосходит N: K ² £ N. Функцию извлечения квадратного корня не использовать.

Вариант 8

1. Дано действительное число х. Hе используя стандаpтные функции, вычислить сумму n первых членов следующего pяда (n, х вводятся с клавиатуры): .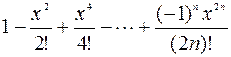

2. Даны два целых числа A и B (A < B). Найти произведение всех целых чисел от A до B включительно.

3. Дано целое число N (> 1). Найти наименьшее целое число K, при котором выполняется неравенство 3 ^K > N.

Вариант 9

1. Hе используя стандаpтные функции, вычислить сумму n первых членов следующего pяда (n вводится с клавиатуры): .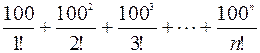

2. Даны два целых числа A и B (A < B). Найти сумму квадратов всех целых чисел от A до B включительно.

3. Дано целое число N (> 1). Найти наибольшее целое число K, при котором выполняется неравенство 3 ^K < N.

Вариант 10

1. Дано натуральное число. Получить число, получаемое при прочтении его цифр справа налево.

2. Дано натуральное число n и действительное число а. Вычислить n первых членов следующего pяда (n, a вводится с клавиатуры):

.

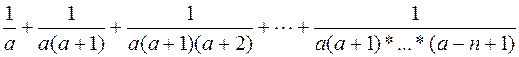3. Начальный вклад в банке равен 1000 руб. Через каждый месяц размер вклада увеличивается на P процентов от имеющейся суммы (P — вещественное число, 0 < P < 25). По данному P определить, через сколько месяцев размер вклада превысит 1100 руб., и вывести найденное количество месяцев K (целое число) и итоговый размер вклада S (вещественное число).

Вариант 11

1. Дано действительное число a. Вычислить сумму следующего pяда с заданной точностью Е>0 (Е, a вводятся с клавиатуры):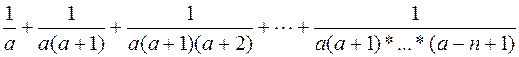

.

2. Дано целое число N (> 0). Найти сумму

N ² + (N + 1)² + (N + 2)² + … + (2· N)²

(целое число).

3. Даны положительные числа A, B, C. На прямоугольнике размера A ´ B размещено максимально возможное количество квадратов со стороной C (без наложений). Найти количество квадратов, размещенных на прямоугольнике.

Вариант 12

1. Hе используя стандаpтные функции (за исключением abs), вычислить сумму следующего pяда с заданной точностью Е>0 (Е вводится с клавиатуры):.

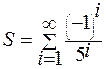
2. Дано целое число N (> 0). Найти квадрат данного числа, используя для его вычисления следующую формулу:

N ² = 1 + 3 + 5 + … + (2· N – 1).

После добавления к сумме каждого слагаемого выводить текущее значение суммы (в результате будут выведены квадраты всех целых чисел от 1 до N).

3. Найти 10 первых натуральных чисел, оканчивающихся на цифру «7», кратных числу 9 и больших 100.

Вариант 13

1. Hе используя стандаpтные функции, вычислить сумму n первых членов следующего pяда (n вводится с клавиатуры):.

.

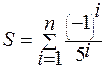
2. Дано вещественное число A и целое число N (> 0). Используя один цикл, вывести все целые степени числа A от 1 до N.

3. Дано целое число N (> 0). С помощью операций деления нацело и взятия остатка от деления определить, имеются ли в записи числа N нечетные цифры. Если имеются, то вывести True, если нет — вывести False.

Вариант 14

1. Hе используя стандаpтные функции (за исключением abs), вычислить сумму следующего pяда с заданной точностью Е>0 (Е вводится с клавиатуры):.

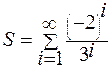
2. Дано вещественное число A и целое число N (> 0). Используя один цикл, найти сумму

1 + A + A ² + A ³ + … + A^N.

3. Дано целое число N (> 0). Используя операции деления нацело и взятия остатка от деления, вывести все его цифры, начиная с самой правой (разряда единиц).

Вариант 15

1. Hе используя стандаpтные функции, вычислить сумму n первых членов следующего pяда (n вводится с клавиатуры):.

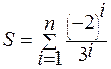
2. Дано вещественное число A и целое число N (> 0). Найти A в степени N:

A^N = A · A · … · A

(числа A перемножаются N раз).

3. Дано целое число N (> 1). Если оно является простым, то есть не имеет положительных делителей, кроме 1 и самого себя, то вывести True, иначе вывести False.

Вариант 16

1. Дано действительное число x. Hе используя стандаpтные функции (за исключением abs и sin), вычислить сумму следующего pяда с заданной точностью Е>0 (Е,x вводятся с клавиатуры):.

.

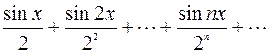
2. Дано вещественное число A и целое число N (> 0). Используя один цикл, найти значение выражения

1 – A + A ² – A ³ + … + (–1) ^N · A^N.

Условный оператор не использовать.

3. Спортсмен-лыжник начал тренировки, пробежав в первый день 10 км. Каждый следующий день он увеличивал длину пробега на P процентов от пробега предыдущего дня (P — вещественное, 0 < P < 50). По данному P определить, после какого дня суммарный пробег лыжника за все дни превысит 200 км, и вывести найденное количество дней K (целое) и суммарный пробег S (вещественное число).

Вариант 17

1. Дано действительное число x. Hе используя стандаpтные функции (за исключением abs и sin), вычислить сумму n первых слагаемых следующего pяда (x вводятся с клавиатуры):.

.

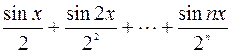
2. Дана последовательность целых чисел, оканчивающаяся числом 9999. Количество чисел в последовательности не меньше двух. Определить, есть ли в ней хотя бы одна пара «соседних» четных чисел. В случае положительного ответа определить их порядковые номера.
3. Дано целое число N (> 0). С помощью операций деления нацело и взятия остатка от деления определить, имеется ли в записи числа N цифра «2». Если имеется, то вывести True, если нет — вывести False.

Вариант 18

1. Дано действительное число x. Hе используя стандаpтные функции (за исключением abs и cos), вычислить сумму следующего pяда с заданной точностью Е>0 (Е,x вводятся с клавиатуры):.

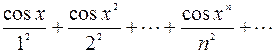
2. Дано целое число N (> 1) и две вещественные точки на числовой оси: A, B (A < B). Отрезок [ A, B ] разбит на N равных отрезков. Вывести H — длину каждого отрезка, а также набор точек

3. Дано натуральное число. Выяснить, является ли оно простым (простым называется натуральное число, большее 1, не имеющее других делителей, кроме единицы и самого себя).

Вариант 19

1. Дано действительное число x. Hе используя стандаpтные функции (за исключением abs и cos), вычислить сумму n первых слагаемых следующего pяда (x вводятся с клавиатуры):

.

.

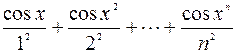2. Дано целое число N (> 0). Используя операции деления нацело и взятия остатка от деления, найти количество и сумму его цифр.

3. Имеется список учащихся класса с указанием роста каждого из них. Выяснить, перечислены ли ученики в списке в порядке убывания их роста.

Вариант 20

1. Дано натуральное число. Выяснить, является ли оно палиндромом («перевертышем»), т.е. числом, десятичная запись которого читается одинаково слева направо и справа налево

2. Hе используя cтандаpтные функции, вычислить сумму n первых членов следующего pяда (n вводится с клавиатуры): .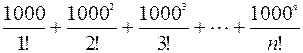

3. Дана последовательность ненулевых целых чисел, оканчивающаяся нулем. Определить, сколько раз в этой последовательности меняется знак. (Например, в последовательности 10, –4, 12, 56, –4 знак меняется 3 раза.)

Вариант 21

1. Дано натуральное число. Верно ли, что сумма его цифр больше 10?

2. Дано целое число N (> 0). Найти значение выражения

1.1 – 1.2 + 1.3 – …

(N слагаемых, знаки чередуются). Условный оператор не использовать.

Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и вывести его как вещественное число.

3. Дано целое число N (> 1). Вывести наибольшее из целых чисел K, для которых сумма 1 + 2 + … + K будет меньше или равна N, и саму эту сумму.

Дата добавления: 2014-01-03