Вырожденный «почти идеальный» Ферми-газ с отталкиванием между частицами

Свойства газа для 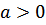и 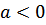будут различны. Начнем со случая .

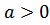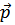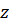Состояние свободной частицы определяется импульсом и – проекцией спина .

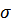В соответствии с этим полагаем

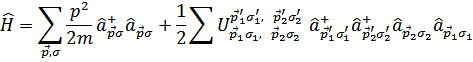
Суммирование по импульсам и 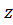– проекциям спина

Как и ранее заменяем матричные элементы на

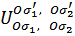
(взаимодействие от проекций спина не зависит)

при равных нулю импульсах частиц в силу антикоммутативности пары одинаковых операторов, обращаются в нуль все слагаемые, содержащие одинаковые пары индексов 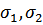или .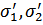

Физически это связано с тем, что рассеиваться могут только частицы с противоположными спинами.

В результате получим гамильтониан в следующем виде

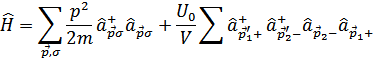
при рассеянии спин не меняется

Суммирование проводится по всем импульсам с учетом законом сохранения

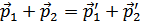
Вычисление собственных значений можно провести с помощью обычной квантово-механической теории возмущений, рассматривая взаимодействие как малую поправку.

Оператор кинетической энергии уже имеет диагональный вид, а его собственные значения равны

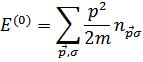
Поправка первого порядка дается диагональными матричными элементами энергии взаимодействия

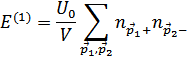
Поправка второго порядка к энергии в состоянии ;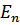

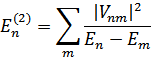
Приводит к результату

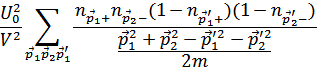
Так как вероятность перехода (квадрат матричного элемента) пропорционально числам заполнения состояний 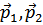и числам «свободных» мест в состояниях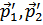

Точно также, члены второго порядка надо учесть более полно по формуле

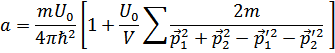
Таким образом, выражая 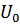через «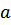» и производя группировку слагаемых разного порядка, получим

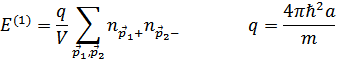
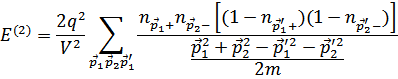
Раскрывая произведения, убеждаемся, что член с произведением четырех «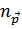» равен нулю (числитель симметричен, знаменатель – антисимметричен по перестановке )

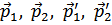Таким образом

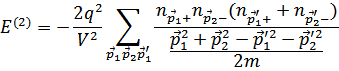
Прежде всего вычислим энергию основного состояния газа. Для этого надо положить числа заполнения квазичастиц 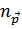(именно после диагонализации гамильтониана по теории возмущений появляются квазичастицы) равными:

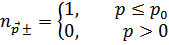
Учтем, что

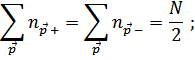
получим

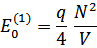
Во втором порядке суммирование заменяем интегрированием, что даст

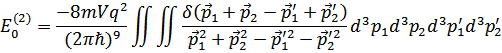
Интегрирование проводится по области
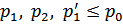, где 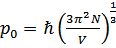– граничный импельс

Таким образом получим

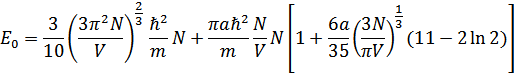
Далее можно найти химический потенциал

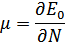
А также, скорость звука в газе

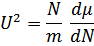
Так как

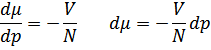
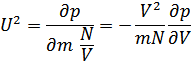
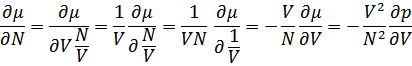
Теперь вычислим функцию взаимодействия квазичастиц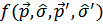

Для этого представим энергию в виде

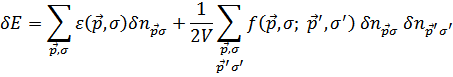
После дифференцирования необходимо заменить ступенькой

Дважды дифференцируем 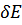и переходим от суммирования к интегрированию, что даст

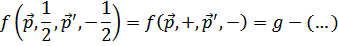
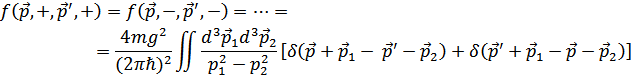
Окончательный результат не должен зависеть от выбора оси 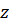. Поэтому

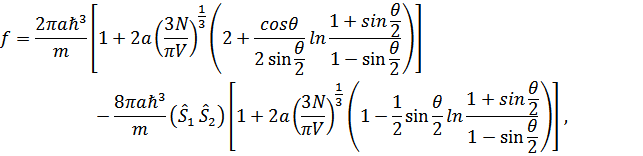
где 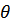– угол между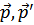

Эффективная масса получается по формуле

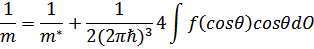
Учитываем, что собственные значения 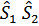равны соответственно 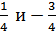для параллельных и антипараллельных спинов.

В результате получим

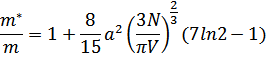
Таким образом, мы вычислим первые члены разложения по степеням .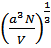

В принципе, можно вычислить ещё несколько членов ряда теории возмущений. Но это уже сложно.

 

Вырожденный «почти идеальный» Бозе – газ

Вопрос о термодинамических свойствах такого газа не имеет непосредственного физического смысла (такое вырождение наступает лишь при низких температурах, но тогда газ конденсируется).

Задача представляет методический интерес. Тем не менее, считаем, что в воображаемой модели взаимодействие организовано так, что конденсация исключается.

Условие «слабой неидеальности» газа заключается в малости действия молекулярных сил «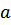» по сравнению со средним расстоянием между частицами 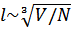. Вместе с условием 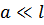будет справедливо неравенство 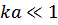, где 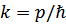– волновое число частиц газа. Мы будем рассматривать лишь парные взаимодействие между частицами. Нам необходимо вычислить первые члены разложения термодинамических величин по степеням 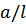в том или ином варианте квантовомеханической теории возмущений. Затруднение заключается в том, что ввиду быстрого нарастания 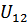на малых расстояниях, теория возмущений (борновское приближение), непосредственно, к столкновениям частиц неприменима. Это затруднение преодолевается следующим образом.

В борновском приближении сечение рассеяния при столкновениях двух частиц дается квадратом модуля «амплитуды рассеяния»

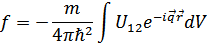
Где 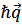– передаваемый при столкновениях импульс. При рассеянии «медленных» частиц, во всей области интегрирования 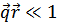. При этом амплитуда рассеяния стремится к постоянному пределу

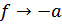
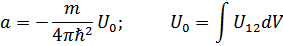
Эта величина должна полностью определять термодинамические свойства газа.

Таким образом, формально заменяем истинную энергию 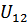другой функцией, с тем же самым значением амплитуды рассеяния, но допускающей применение теории возмущений. До тех пор, пока окончательный результат будет содержать 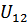в виде амплитуды рассеяния, этот результат будет совпадать с тем, к которому привело бы истинное взаимодействие.

Начнем с задачи о вычислении энергетического спектра слабо возбужденных состояний почти идеального Бозе-газа. Это можно сделать применением теории возмущений в методе вторичного квантования.

Гамильтониан системы 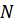бесспиновх частиц в методе вторичного квантования имеет вид

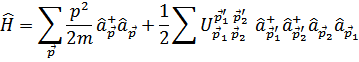
Здесь 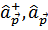– операторы рождения и уничтожения свободной частицы с импульсом 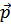, т.е. в состоянии описываемом волновой функцией

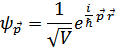
Первый член – кинетическая, второй – потенциальная энергия. Суммирование проводится по всем значениям импульсов пар частиц, с соблюдением закона сохранения импульса при столкновениях

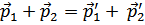
Только при этом условии отличны от нуля матричные элементы

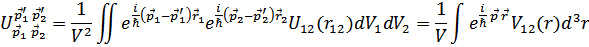
Где 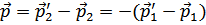– изменение импульса частиц при столкновениях. Поскольку мы предполагаем импульсы малыми, то в матричных элементах можно полагать 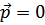, т.е.

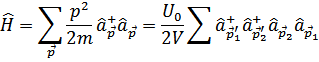
Исходным пунктом применения теории возмущений таково: в основном состоянии идеального Бозе-газа все частицы находятся в «конденсате» - состоянии с нулевой энергией:

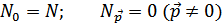
В почти идеальном газе в слабовозбужденных состояниях (и в основном) числа заполнения 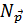отличны от нуля. Но очень малы по сравнению с 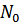. Тот факт, что величина 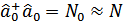весьма велика по сравнению с единицей, означает, что выражение 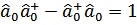мало по сравнению с 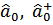а поэтому операторы можно рассматривать как обычные числа (равные 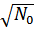) пренебрегая их некоммутативностью.

Применение теории возмущений означает теперь формально разложение четверной суммы по степеням малых величин 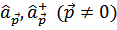. Нулевой член разложения равен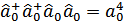

Члены первого порядка отсутствует ввиду невозможности соблюдения в них закона сохранения импульса. Члены второго порядка есть

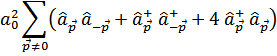
Ограничившись точностью до членов второго порядка можно заменить
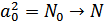. В члене второго порядка следует учесть более точное соотношение

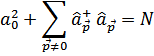
В результате сумма членов равна

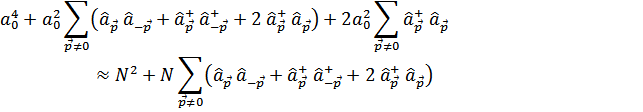
В результате получим следующее выражение для гамильтониана

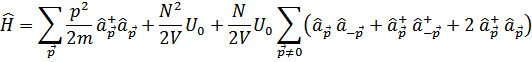
Интеграл 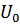должен быть выражен через амплитуду рассеяния. В членах второго порядка по 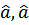это можно сделать непосредственно из определения амплитуды рассеяния. В членах нулевого порядка по 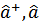(т.е. 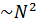) эта формула, отвечающая лишь первому приближению теории возмущений, недостаточно точна.

Вспомним, что вероятность перехода под влиянием возмущения 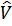во втором порядке

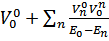суммирование по всем состояниям невозмущенной системы

Здесь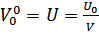

Воспользовавшись другими матричными элементами полагаем, что

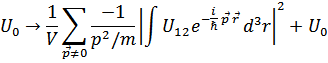
Или, снова как ранее, заменяя интегралы на 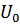, получим

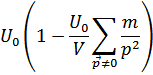
Поэтому вместо

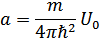
Будем иметь

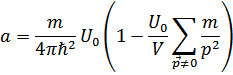
Или с той же точностью

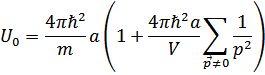
В результате гамильтониан примет вид

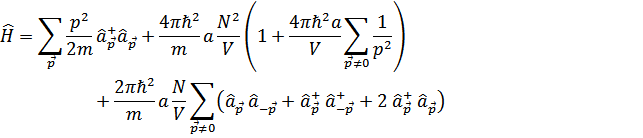
Для определения уровней энергии гамильтониана надо привести к диагональному виду, что осуществляется линейным преобразованием операторов .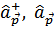

Рассмотрим новые операторы 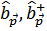согласно соотношениям

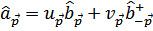
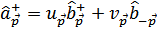
Потребуем, чтобы они удовлетворяли таким же соотношениям коммутации, каким удовлетворяют операторы 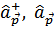, т.е.

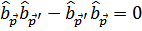
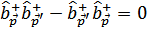
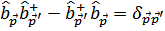
Легко видеть, что для этого должно быть

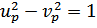
Учтем это, записав преобразование в виде

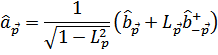
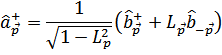
Величину 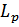надо определить таким образом, чтобы в гамильтониане выпали недиагональные члены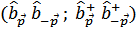

Простое вычисление даст

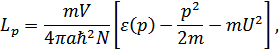
где введены обозначения

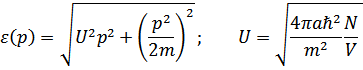
Тогда гамильтониан принимает вид

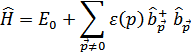
Здесь

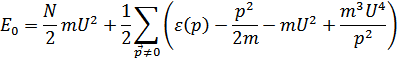
представляет собой энергию основного состояния газа. Операторы 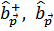представляют собой операторы «рождения» и «уничтожения» квазичастиц (элементарных возбуждений) с энергией 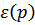, подчиняющихся статистике Бозе.

Тогда величина 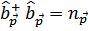представляет собой число квазичастиц с импульсом 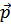. Отметим, что мы по-разному обозначаем числа заполнения квазичастиц 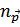в отличии от чисел заполнения истинных частиц газа 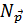. Таким образом, полностью определен энергетический спектр слабо возбужденных состояний. Это спектр бозевского типа.

Заменяя в определении 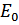суммирование – интегрированием по 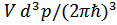, получим

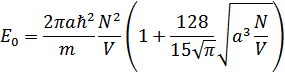
При больших значениях импульса (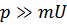) энергия квазичастиц стремиться к 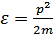, т.е. к кинетической энергии отдельной частицы газа.

При малых же импульсах (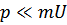) имеем 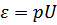, где 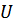– скорость звука в газе. При 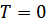свободная энергия равна энергии 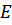. Тогда, находим давление

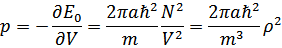
В то же время скорость звука есть

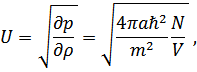
что совпадает с прежним определением. Отметим, что 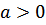(отталкивание между частицами) иначе появятся мнимые величины (скорость) с другой стороны условие 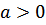обеспечивает термодинамическое неравенство 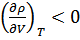, что необходимо для термодинамической устойчивости системы (механической)

Статистическое распределение элементарных возбуждений (при 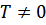) задается формулой Бозе (с равным нулю химическим потенциалом)

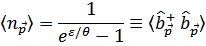
Распределение же истинных частиц по импульсам вычисляется как

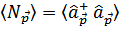
Подставляя сюда определение 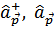через операторы 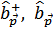и учитывая их соотношения коммутации, получим

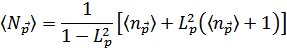
Это выражение справедливо лишь при 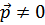. Число же частиц с нулевым импульсом

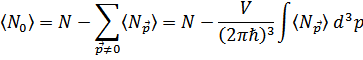
В частности, при 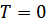имеем 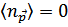при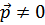

В результате

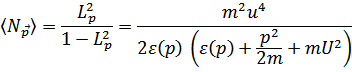
Тогда число частиц с нулевым импульсом равно

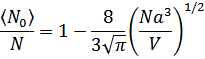
Сделаем следующее замечание. При малых 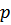производная 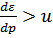(т.е. кривая 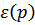загибается вверх начальной касательной 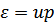). Это означает, что законы сохранения энергии и импульса допускают самопроизвольный распад квазичастицы (фононы) на две. То есть данный спектр с самого начала является неустойчивым. Элементарные возбуждения в нем имеют конечное время жизни. Для реального спектра такой неустойчивости нет.

 

 

ТЕМА №8