Функция Грина макроскопической системы

Разработанный ранее метод становится громоздким и практически неприменимым в высших порядках теории возмущений. Это тем более существенно, что в реальных физических задачах взаимодействие между частицами отнюдь не является слабым, поэтому требуется вычисление бесконечной совокупности ряда теории возмущений.

Существует специальная техника, подобная той, которая в квантовой теории поля.

Конкретная форма этого аппарата зависит от характера макроскопической системы, к которой она применяется. Мы будем рассматривать ферми-жидкость при .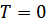

Исходным материалом служат вторично-квантованные 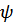– операторы. Нам понадобятся эти операторы в гейзенберговском представлении, в котором они явно зависят от времени.

Мы будем рассматривать системы, состоящие из частиц со спином .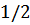

Соответственно будем приписывать оператору спиновый индекс.

Вспомним, что оператор любой физической величины в гейзенберговском представлении, выражается через независящий от времени (шрединговский) оператор той же величины согласно

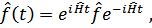
где 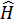– гамильтониан системы.

Как и ранее, удобно перейти к оператору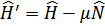

Таким образом, определим гейзенберговские операторы

– гейзенберговский оператор; 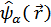– шредингеровский оператор.

Шредингеровские 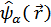операторы удовлетворяет известным правилам коммутации. Гейзенберговские операторы, взятые в произвольные моменты времени, вычислить в общем виде невозможно. Однако, при их правило коммутации совпадает с правилом для шредингеровских операторов.

Так, из правила

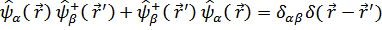
следует аналогичное правило

Таким же образом для одинаковых операторов

Дифференцируя определение 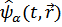по времени, найдем уравнение движения

Оба представления тождественны для оператора всякой сохраняющейся величины, т.е. оператора, коммутативного гамильтониану. Это относится и к самому гамильтониану, и к оператору числа частиц – точнее сохраняющейся величины, которая есть

по индексу 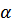– суммирование.

Гамильтониан системы взаимодействующих частиц имеет вид

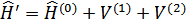
Здесь – гамильтониан системы свободных частиц; – гамильтониан их взаимодействия с внешним полем 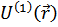; 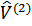– оператор парного взаимодействия частиц. Считаем, что взаимодействие от спина частиц не зависит.

Правая часть уравнения движения (коммутатор ) вычисляется с помощью правил коммутации.

Возникающие – функции устраняются интегрированием. В результате получаем уравнение Шредингера для в виде

Получилось нелинейное интегродифференциальное уравнение. Необходимо задать начальные условия. (Эволюция, начальные условия, спектр элементарных возбуждений, работа Боголюбова 1964 года).

Основную роль играет понятие функции Грина макроскопической системы. Она определяется следующим образом

Здесь обозначает совокупность момента времени и радиус – вектор точки 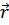. Угловые скобки означают усреднение по основному состоянию (вместо более громоздкого обозначения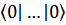). Символ 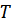– знак хронологического произведения: следующие за ним операторы должны быть расположены справа налево в порядке возрастания времени .

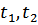При этом, в случае фермионов перестановки пары 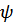– операторов (по сравнению с первоначальной записью) должно сопровождаться изменением знака произведения в явном виде это значит, что

Отметим некоторые очевидные свойства. Если система не ферромагнитная и не находится во внешнем поле, то спиновая зависимость функции Грина сводится к единичной матрице

В силу однородности времени, моменты 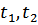входят в функцию Грина лишь в виде разности . Если же, система макроскопически однородна в простанстве, то в виде разности 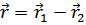входят и координаты двух точек. Таким образом, в этом случае

Тело однородно не велико по своей средней (макроскопической) плотности, но и по плотности вероятности различных (микроскопических) положений её частиц в пространстве (газа, жидкости, но не кристалла).

В силу изотропии, получим .

В то же время не является четной по перестановке времени : порядок времен в разности 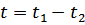существенен.

Далее вспомним, что координатная матрица плотности определяется как среднее значение

Знание этой матрицы позволяет определить среднее значение любой величины, относящейся к отдельной частице.

Пусть 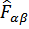– некоторый оператор «одночастичный»

– действует на координаты и спин отдельной частицы.

В то же время в методе вторичного квантования (в гейзенберговском представлении) такой оператор есть

Отсюда видно, что среднее значение величины 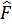может быть выражено в терминах матрицы плотности как

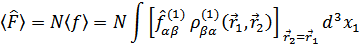
Полагаем 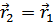после действия оператора , но перед интегрированием по .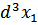

Согласно определению функции Грина 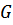, имеем её связь с матрицей плотности

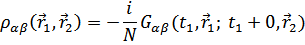
означает предел сверху (обеспечивается правильное соответствие с определением )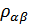

Для макроскопически однородной системы матрица плотности зависит также от разности и не зависит от спиновых индексов:

Здесь мы обозначаем .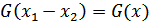

Легко убедиться (при 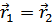и после взятия следа по спиновым переменным, произведение операторов в определении 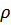превращается в 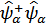– оператор плотности числа частиц в системе)

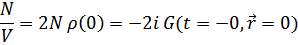
(стремится к нулю снизу). Это равенство связывает химический потенциал 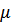(при 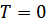), от которого 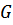зависит как от параметра, с плотностью числа частиц через уравнение «движения».

Далее, вспомним, что Фурье-разложение матрицы плотности определяет распределение частиц по импульсам (фурье-компонента матрицы совпадает с выражением ).

Поэтому распределение

Частиц по импульсам можно выразить также через функцию Грина

Это есть число частиц (в единице объема) с определенным значением проекции спина и импульсами в интервале .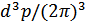

Подчеркнем, что речь идет об истинных частицах, а не о квазичастицах (последние пока не появились). Поэтому и введем обозначения вместо .

В дальнейшем обычно рассматривают функцию Грина в импульсном представлении (фурье-компоненты)

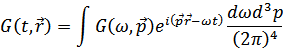
(там происходит переход к квазичастицам)

Тогда распределение частиц по импульсам выражается через эту фурье-компоненту 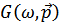следующим образом

Что доказывается непосредственной подстановкой.

Нормировка фурье-компоненты определяется формулой

(получается из определения средней плотности тела через функцию Грина).

Таким образом распределение автоматически правильно нормировано

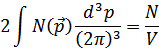
Определение энергетического спектра по функции Грина.

Исследование аналитических свойств функции Грина показывает, что

Главные свойства функции Грина в импульсном представлении заключаются в том, что её полюса могут лежать только в точках , где 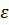– дискретные энергии возбуждения системы. Каждая из этих энергий отвечает определенному значению импульса системы 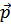, приписанному одной квазичастице.

Таким образом, уравнение

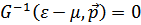
определяет закон дисперсии квазичастицы.

Функция Грина идеального ферми-газа.

Напомним, что шредингеровские 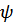– операторы всегда можно представить в виде разложения

По полному набору функций – волновых функций свободных частиц с импульсом 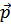и энергией 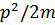, т.е. по плоским волнам

– спиновая амплитуда, такая что .

Такой выбор функций не имеет отношения к реальному взаимодействию частиц в системе. Но для системы невзаимодействующих частиц может быть записан в явном виде также и гейзенберговский 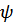– оператор.

В этом случае

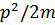(– собственное значение гамильтониана 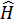для свободных частиц) (переход к системе с переменным числом частиц).

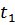Однако, вместо прямого вычисления функции Грина в соответствии с определением, удобно перейти к рассмотрению эквивалентного уравнения. Для этого продифференцируем функцию по времени . При этом надо учесть, что в точке эта функция разрывна.

Действительно, согласно определению, скачок функции равен

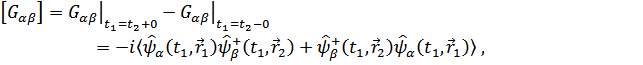
что с учетом коммутационных соотношений для гейзенберговских 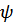– операторов дает

Наличие скачка приводит при дифференцировании по 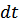к появлению дополнительного члена . Поэтому

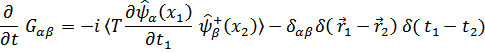
Для системы свободных частиц гейзенберговский 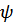– оператор удовлетворяет уравнению

Подставляя эту производную в уравнение и снова воспользовавшись определением , получим

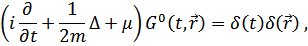
где мы обозначим

Преобразование фурье дает следующий результат

ТЕМА №11

Вычисление термодинамических величин по функции Грина.

После того, как определен закон дисперсии из уравнения

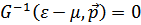
Находим химический потенциал из условия

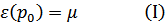
Поскольку

Или

То подставляя 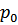в , получим неявное определение .

Поскольку при 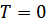имеем 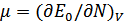(– энергия основного состояния), то интегрируя, найдем искомую энергию

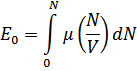
После этого можно найти остальные термодинамические величины.

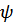– операторы в представлении взаимодействия.

Гриновскую функцию системы взаимодействующих частиц нельзя вычислить в общем виде. Существует, однако, техника, которая позволяет вычислять её в виде ряда по степеням энергии взаимодействия. При этом каждый член ряда выражается через функцию Грина системы свободных частиц и оператор взаимодействия.

Рассмотрим такие представления взаимодействия

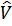– оператор взаимодействия; – гамильтониан свободных частиц

Тогда операторы в представлении взаимодействия выражаются через шредингеровские операторы

В представлении взаимодействия удобно перейти к функциям, действующим в пространстве чисел заполнения 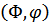; на эти функции действуют вторично-квантованные операторы.

Пусть 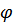– такая функция в шредингеровском представлении; её зависимость от времени

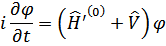
В гейзенберговсом представлении вся временная зависимость перенесется на операторы, а волновая функция системы не зависит от времени .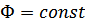

В представлении взаимодействия волновая функция зависит от времени, но эта зависимость обязана только со взаимодействием частиц в системе

И определяется уравнением

где

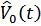– оператор взаимодействия

Данное уравнение легко получить, заметив, что записанное ранее преобразование оператора соответствует преобразованию волновых функций согласно

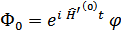
дифференцируя это выражение учитывая уравнение для 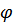, получим вышенаписанное.

В силу значения в два бесконечно близких момента времени связаны друг с другом равенством

Поэтому значение в произвольный момент может быть выражено через значение в некоторый начальный момент как

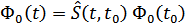
Где

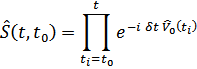
Сомножители в этом произведении расположены справа налево, в порядке возрастания времен 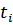(подразумевается предел произведения по всем бесконечно малым между и ).

Если бы 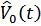было обычной функцией, то этот предел сводился бы к

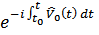
Но такой предел основан на коммутативности сомножителей, взятых в различные моменты времени, подразумевающийся при переходе от произведения к суммированию в показателе экспоненты. Для оператора 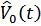такой коммутативности нет и переход к обычному интегралу невозможен. Вместо этого можно записать в символическом виде

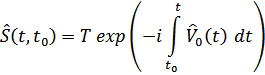
где 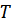– символ хронологического произведения множителей в той же последовательности: справа налево, в порядке возрастания времени.

Оператор унитарен и обладает очевидным свойствами

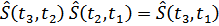
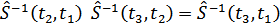
Для упрощения выкладок (конечный результат от этого не зависит) считаем, что взаимодействие адиабатически «включается» при и адиабатически «выключается» при .

Тогда при (до выключения взаимодействия) волновая функция совпадает с гейзенберговской функцией 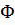. Поэтому полагая , получим

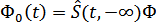
Таким образом, установлена связь между волновыми функциями в представлении взаимодействия и гейзенберовском представлении в результате устанавливается связь между операторами в этих представлениях

В силу унитарности , по такому же закону преобразования оператора .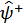

Теперь можно выразить функцию Грина в представлении взаимодействия

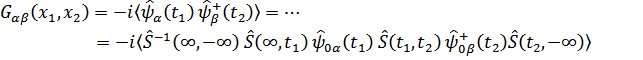
Все множители, начиная со второго, расположены в хронологическом порядке справа налево от до .

Поэтому можно записать

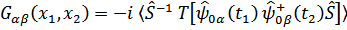
где

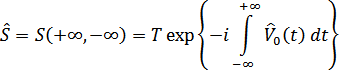
Дата добавления: 2014-01-03