Воспроизведение непрерывного сигнала

Воспроизведение непрерывного сигнала по выборкам может проводиться как на основе ортогональных, так и неортогональных базисных функций. Воспроизводящая функция s'(t) соответственно представляется аппроксимирующим полиномом:

s'(t) =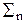c_n v_n(t), (7.2)

где v_n(t) – система базисных функций.

Ортогональные базисные функции обеспечивают сходимость ряда к s(t) при n Þ ¥. Оптимальными являются методы дискретизации, обеспечивающие минимальный числовой ряд при заданной погрешности воспроизведения сигнала. При неортогональных базисных функциях используются, в основном, степенные алгебраические полиномы вида:

s'(t) =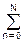c_n tⁿ. (7.3)

Если значения аппроксимирующего полинома совпадают со значениями выборок в моменты их отсчета, то такой полином называют интерполирующим. В качестве интерполирующих полиномов обычно используются многочлены Лагранжа. Для реализации интерполирующих полиномов необходима задержка сигнала на интервал дискретизации, что в системах реального времени требует определенных технических решений. В качестве экстраполирующих полиномов используют, как правило, многочлены Тейлора.

Естественным требованием к выбору частоты дискретизации является внесение минимальных искажений в динамику изменения сигнальных функций. Логично полагать, что искажения информации будут тем меньше, чем выше частота дискретизации F. С другой стороны также очевидно, что чем больше значение F, тем большим количеством цифровых данных будут отображаться сигналы, и тем большее время будет затрачиваться на их обработку. В оптимальном варианте значение частоты дискретизации сигнала F должно быть необходимым и достаточным для обработки информационного сигнала с заданной точностью, т.е. обеспечивающим допустимую погрешность восстановления аналоговой формы сигнала (среднеквадратическую в целом по интервалу сигнала, либо по максимальным отклонениям от истинной формы в характерных информационных точках сигналов).

Дата добавления: 2014-01-03