Решение. Мы используем таблицу, подобную той, которую мы применяли раньше при r1 = 26 и r2 = 12. q r1 r2 r t1 t2 t

Пример

Найти инверсию 12 в Z₂₆.

Мы используем таблицу, подобную той, которую мы применяли раньше при r₁ = 26 и r₂ = 12.

q	r1	r2	r	t1	t2	t
					-2
				-2

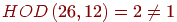, что означает отсутвствие для числа 12 мультипликативной инверсии в Z₂₆

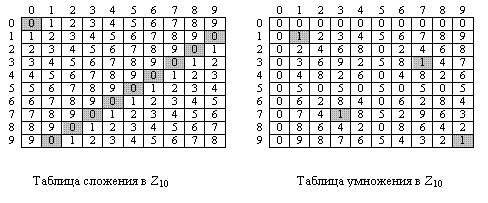
Сложение и умножение таблиц

Рисунок показывает две таблицы для сложения и умножения. При сложении таблиц каждое целое число имеет аддитивную инверсию. Обратные пары могут быть найдены, если результат их сложения — ноль. Мы имеем (0, 0), (1, 9), (2, 8), (3, 7), (4, 6) и (5, 5). При умножении таблиц мы получаем только три мультипликативных пары (1, 1), (3, 7) и (9, 9). Пары могут быть найдены, когда результат умножения равен 1. Обе таблицы симметричны по диагонали, от левой вершины к нижней вершине справа. При этом можно обнаружить свойства коммутативности для сложения и умножения (a+b = b+a и ). Таблица сложения также показывает, что каждый ряд или колонка может поменяться с другим рядом или колонкой. Для таблицы умножения это неверно.

Различные множества для сложения и умножения

В криптографии мы часто работаем с инверсиями. Если отправитель посылает целое число (например, ключ для шифрования слова), приемник применяет инверсию этого целого числа (например, ключ декодирования). Если это действие (алгоритм шифрования/декодирования) является сложением, множество Z_n может быть использовано как множество возможных ключей, потому что каждое целое число в этом множестве имеет аддитивную инверсию. С другой стороны, если действие (алгоритм шифрования/декодирования) — умножение, Z_n не может быть множеством возможных ключей, потому что только некоторые члены этого множества имеют мультипликативную инверсию. Нам нужно другое множество, которое является подмножеством Z_n и включает в себя только целые числа, и при этом в Z_n они имеют уникальную мультипликативную инверсию. Это множество обозначается Z_n*. Ниже показаны некоторые случаи двух множеств. Обратите внимание, что множество Z_n* может быть получено из таблицы умножения типа показанной на рисунке выше.

Каждый член Z_n имеет аддитивную инверсию, но только некоторые члены имеют мультипликативную инверсию. Каждый член Z_n* имеет мультипликативную инверсию, но только некоторые члены множества имеют аддитивную инверсию.

Мы должны использовать Z_n, когда необходимы аддитивные инверсии; мы должны использовать Z_n*, когда необходимы мультипликативные инверсии.

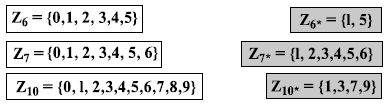
Дата добавления: 2014-01-03