Применение стандартного нормального распределения

Нормальному распределению подчиняются многие встречающиеся на практике случайные величины, образованные в результате суммирования большого числа независимых (или слабо зависимых) случайных величин, подчиненных различным законам распределения.

Если ни одна из этих случайных величин не превалирует над всеми другими, то особенности их распределения в сумме большого числа слагаемых нивелируются и сумма оказывается подчиненной закону, близкому к нормальному закону распределения. Вследствие этого нормальное распределение служит приемлемой моделью для многих физических явлений.

В качестве примера отметим, что нормальному распределению подчинены:

ü -случайные ошибки измерений;

ü -отклонения параметров изделий (размер, масса, толщина покрытия и др.) от среднего значения в серийном производстве;

ü -стабильность технологических процессов.

Биномиальное распределение при 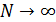, стремится к нормальному распределению с математическим ожиданием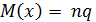и дисперсией 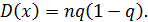Это приближение применяется при условии nq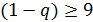. Поэтому нормальное распределение можно использовать для описания не только непрерывных, но и для дискретных величин.

Любую случайную величину, имеющую нормальное распределение, можно нормировать с помощью линейного преобразования: (см. формулу 24)

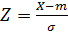(27)

При этом все возможные варианты нормального распределения сводятся к так называемому нормированному (стандартному) нормальному распределению. Выражение для плотности такого распределения получают из (22) если в это выражение подставить Z

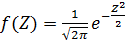(28)

Функция нормированного (стандартного) нормального распределения, называемая нормальной функцией распределения (функцией Лапласа), имеет вид:

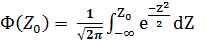(29)

С помощью табулированных значений функции (29)) нетрудно вычислить значения функции

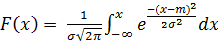
для любых значений х иσ, учитывая, что.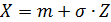

Для заданного Z = Z₀ значению функции нормированного нормального распределения Ф(Z₀) на рис. 6 соответствует заштрихованная площадь под графиком плотности нормированного нормального распределения (вся площадь под этим графиком независимо от величины σ равна единице), т.е. значение площади, лежащей левее точки Z₀.

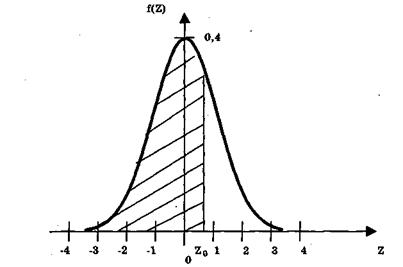
Рисунок 6. - Значение функции нормированного нормального распределения Ф(Z₀) для заданного Z = Z₀

Нормальное распределение обладает важным свойством, которое используется в управлении качеством процессов и продукции: - большинство наблюдаемых значений случайной величины, подчиняющейся этому закону распределения, группируются вблизи математического ожидания, а по мере удаления от него встречаются все реже, а именно:

68,27%, т.е. две трети всех значений случайной величины расположены в полосе от –σ до +σ;

95% -в полосе от–1,96σ до +1,96σ;

95,45% - в полосе от –2σ до +2σ;

99% - в полосе от –2,576σ до +2,576σ;

99,73% -в полосе от –3σ до +3σ;

99,9% - в полосе от –3,291σ до +3,291σ;;

99,994% - в полосе от –4σ до +4σ. –

Точки перегиба кривой нормального распределения находятся на расстоянии .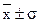

Здесь уместно напомнить известное в математической статистике "правило трех сигм. Действительно, при нормальном распределении трех-сигмовые границы охватывают 99,73% всех результатов измерений. Это означает, что при проведении 10000 измерений в среднем только в 27 случаях результаты измерений будут находиться за пределами трехсигмовых границ, или при 370 измерениях - один результат.

Дата добавления: 2014-01-03