Двойной интеграл в полярных координатах

Лекция 5. Замена переменных в кратных интегралах. Якобиан и его геометрический смысл. Полярные, цилиндрические и сферические координаты в двойных и тройных интегралах. Площадь поверхности и её вычисление

Приложения кратных интегралов

О двух приложениях было сказано выше, когда обсуждался вопрос о геометрическом смысле двойного интеграла (объём цилиндрического тела) и механическом смысле тройного интеграла (масса тела). Укажем ещё на некоторые другие приложения.

1. Масса плоской пластинки с плотностью 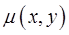в точке 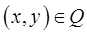вычисляется по формуле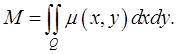

2. Площадь плоской области 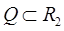можно вычислить по формуле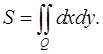

3. Объём тела 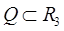можно вычислить тройным интегралом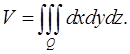

Немного позже будет дано понятие площади произвольной поверхности. Будет показано, что если поверхность 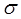задана уравнением 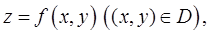то её площадь можно вычислить по формуле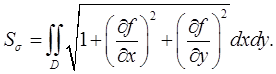

Пример 5 ( Кузнецов Л.А. Типовые расчеты ). Пластинка 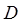задана ограничивающими ее кривыми, 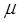-поверхностная плотность. Найти массу пластинки.

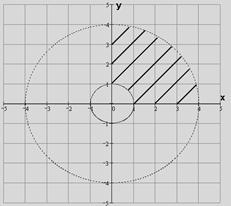
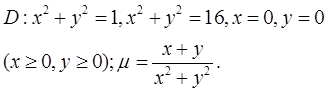
Решение. Вычисляем массу пластинки по фор-

муле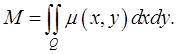Введем полярную система координат: 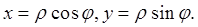Учи-

тывая формулу (4) записи двойного интеграла в полярных координатах, будем иметь

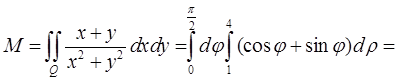
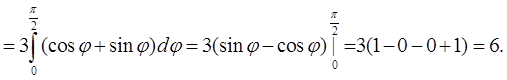
Пример 6 ( Кузнецов Л.А. Типовые расчеты ). Найти объем тела, заданного ограничиваю-

щими его поверхностями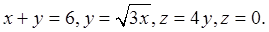

Решение. Объём тела вычисляем тройным интегрированием: 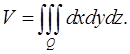Проекцией данного тела на плоскость 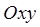является область 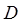с границей 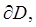описываемой уравнениями 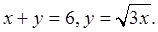Расставляем в 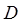пределы по 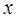и 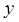в повторных интегралах, предварительно вычислив точку 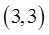пересечения кривых 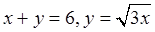и используя описанную ранее методику. Затем через произвольную точку 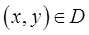проводим луч в направлении оси 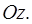Она пересечет нижнюю границу области в точке 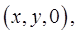а верхнюю границу этой области – в точке 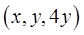. Значит, нижний 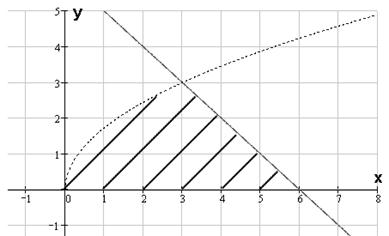предел интеграла по 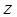будет 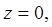а верхний предел по 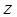будет 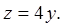В результате получим

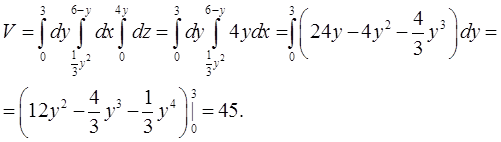
Ранее упоминалось, что некоторые двойные интегралы удобно вычислять в полярных координатах. В отличие от прямоугольных декартовых координат полярные координаты являются криволинейными. Перейдем к описанию криволинейных координат общего вида.

1. Криволинейные координаты на плоскости

Пусть в плоскости 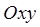задана некоторая область 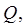а в плоскости 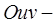некоторая область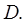

Определение 1. Говорят, что функции

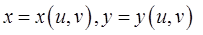
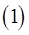
задают взаимно однозначное соответствие области 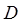на область 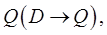если каждой точке 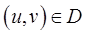соответствует единственная точка 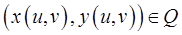и двум различным точкам из области 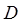соответствуют две различные точки из области по закону (1).

Ясно, что в этом случае существует и обратное отображение 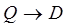, задаваемое некоторыми функциями 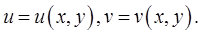Если (1) задаёт взаимно однозначное соответствие 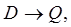то положение любой точки 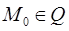фиксируется её декартовыми координатами 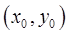или парой чисел 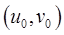такой, что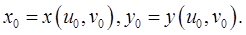

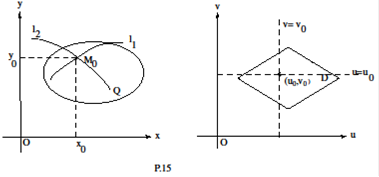
Определение 2. Пара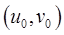 только что описанныхчисел называется криволинейными координатами точки 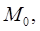а кривые

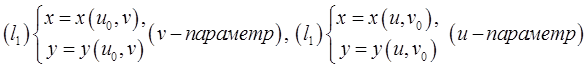
называются координатными линиями точки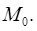

Таким образом, в области можно задать две системы координат: 1) декартову прямоугольную систему координат, определяемую сеткой взаимно ортогональных прямых 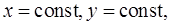и криволинейную систему координат, определяемую сеткой координатных лини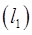й и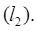

Определение 3. Определитель 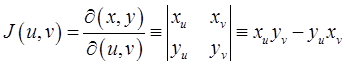называется якобианом отображения (1) или якобианом перехода от декартовых координат к криволинейным.

Можно показать, что 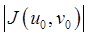равен коэффициенту искажения площадей (геометрический смысл якобиана), т.е. если 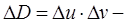площадь малого прямоугольника с одной из вершин 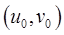и ребрами 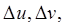а 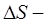площадь криволинейного четырёхугольника, являющегося образом указанного прямоугольника при отображении (1), то 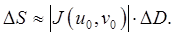Используя этот факт, можно доказать следующее утверждение.

Теорема 1. Имеет место равенство

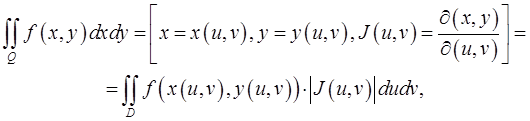
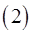
если выполнены следующие условия:

1) функция 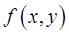непрерывна в замкнутой ограниченной области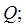

2) функции 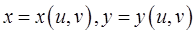непрерывно дифференцируемы в области 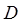и взаимно однозначно отображают область 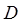на область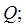

3) якобиан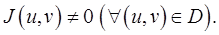

Рассмотрим функции 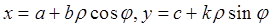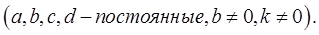Эти функции будут взамно одноз-

начно отображать плоскость переменных 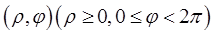на плоскость переменных 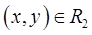, если условиться, что точка 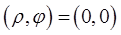переходит только в точку 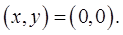Криволинейные координаты 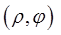называют в этом случае обобщенными полярными координатами, а в случае 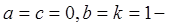просто полярными координа-тами в плоскости 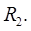Вычислим якобиан перехода для таких координат. Имеем

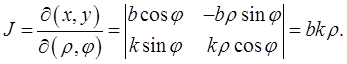
Из теоремы 1 вытекает, что двойной интеграл в обобщенных полярных координатах будет таким:

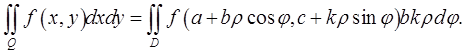
При 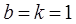получаем формулу

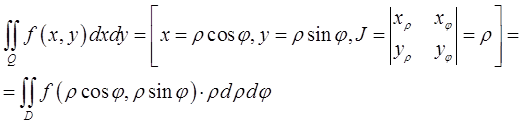
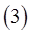
для двойного интеграла в полярных координатах. Здесь и выше 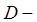область, которая при отображении 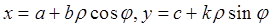переходит в область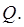

Пример 1 (( Кузнецов Л.А. Типовые расчеты ). Пластинка 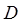задана неравенствами 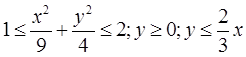, 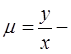поверхностная плотность. Найти массу пластинки.

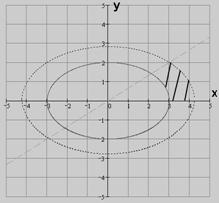Решение. Введем обобщенные полярные координаты

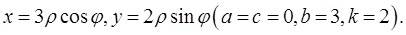
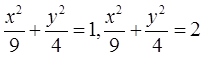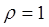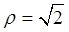При этом эллипсы перейдут в прямые и соответственно, а прямая 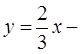в луч 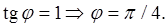Якобиан перехода будет таким: 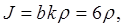поэтому

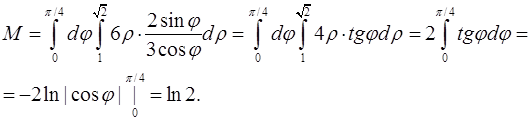
Дата добавления: 2014-01-03