Высокочастотный фильтр Баттеруорта

Синтез фильтров методом частотного преобразования. Высокочастотные и полосовые фильтры конструируются путем частотной трансформации передаточных функций фильтров низких частот. Если обозначить аргумент передаточных функций ФНЧ через p=jW, a функций ФВЧ и ПФ через s=jw, то всегда можно найти такую функцию частотного преобразования p=F(s), которая превращает один тип фильтров в другой. Для преобразования ФНЧ → ФВЧ функция частотного преобразования имеет вид:

p = 1/s, (10.2.1)

В этом нетрудно убедиться сравнением двух видов преобразования. Как известно, передаточная функция ФВЧ может быть получена из ФНЧ разностью между широкополосным фильтром (H(w)=1) и ФНЧ. Применяя этот метод для функции Баттеруорта, получаем:

|H(w)|² = 1-|H(W)|² = 1- 1/(1+W^2N) = W^2N/(1+W^2N). (10.2.2)

С другой стороны, при W = p/j: |H(p)|² = 1/(1-p^2N). Выполняя подстановку (10.2.1) в это выражение, получаем:

|H(s)|² = s^2N/(s^2N-1).

Возвратимся из последнего выражения к аргументу w с учетом принятого равенства s=jw:

|H(s)|² = (jw)^2N/((jw)^2N-1) =(w)^2N/(1+(w)^2N),

что полностью повторяет (10.2.2) при w=W.

Подставляя p=1/s непосредственно в выражение H(p) (10.1.16) для четного значения N, получаем:

H(s) = G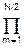s²/(s²+a_m s+1). (10.2.3)

Для нечетного N:

H(s) = [G·s/(s+1)]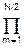s²/(s²+a_m s+1). (10.2.4)

После билинейного z-преобразования выражения с подстановкой s=g(1-z)/(1+z), для четного и нечетного значений N соответственно:

H(z) = G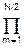g²·G_m·(1-z)²/(1-b_m z+c_m z²). (10.2.5)

H(z) = G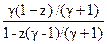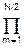g²·G_m·(1-z)²/(1-b_m z+c_m z²). (10.2.6)

G_m = 1/(g² + a_mg + 1). (10.2.7)

b_m = 2·G_m (g² - 1).

c_m = G_m (g² - a_mg + 1).

Значения коэффициентов G_m, b_m, c_m остаются без изменения (сравнить с (10.1.21-10.1.23)). При задании частотных параметров ФВЧ в том же виде, что и для ФНЧ, формула расчетов N и w_dc получается аналогично ФНЧ, при этом в знаменателе выражения (10.1.6) отношение w_dp/w_ds заменяется на w_ds/w_dp:

N = ln [d/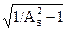] / ln(w_ds/w_dp), (10.2.8)

а в (10.1.7) деление членов правой части меняется на умножение:

w_dc = w_dp·d^1/N. (10.2.9)

Уравнение рекурсивной фильтрации для m-го оператора фильтра:

y_k = g²·G_m (x_k-2x_k-1+x_k-2) + b_m y_k-1 - c_m y_k-2. (10.2.10)

Уравнение рекурсивной фильтрации для дополнительного h₀(i) линейного оператора фильтра при нечетном N:

y₀ = g·(x_k-x_k-1)/(g+1) + y_k-1·(g-1)/(g+1). (10.2.11)

Дата добавления: 2014-01-03