Термодинамическое рассмотрение природы упругих сил

Два типа упругих тел и характер высокоэластической деформации

По признаку характера деформации различают два типа упругих тел – упругие твердые тела и высокоэластичные полимеры.

В упругих твердых телах деформация подчиняется закону Гука (σ = ε D), т.е. пропорциональна приложенному напряжению, причем большим значениям напряжения соответствуют малые (0,1%) деформации. Модуль упругости велик, и для металлов, например, составляет 10 000-20 000 кг/мм² (~10⁵ мПа).

В высокоэластических полимерах упругая деформация может достигать многих сотен процентов при сравнительно низких напряжениях (явление эластичности). Эта деформация является обратимой, но весьма медленно изменяющейся во времени, т.е. носит релаксационный характер. Модуль упругости для вулканизированных каучуков составляет величину ε=0,8 кг/мм² (8 мПа).

Существование двух типов упругих тел (и упругости двух типов) можно объяснить при термодинамическом рассмотрении процесса высокоэластической деформации.

Пусть эластомер длиной l ₀ под действием силы f удлинился на величину dl. Так как эластомеры практически не меняют объема при деформации, работа деформации образца dA обусловлена только действием приложенной силы:

.

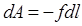Согласно первому закону термодинамики для изолированных систем разность полученной системой теплоты Q и произведенной ею работы А не зависит от условий проведения процесса, а определяется только исходным и конечным состояниями системы:

,

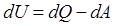где Q – теплота; U – внутренняя энергия; A – работа. Внутренняя энергия складывается из теплоты, подведенной к системе, и работы, совершенной над системой.

Для нашего случая деформации образца

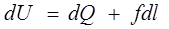. (6)

Кроме того, согласно закону термодинамики любой самопроизвольный процесс сопровождается увеличением энтропии:

.

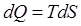Подставив это выражение в уравнение (6), получим

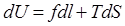. (7)

Cогласно второму закону термодинамики внутренняя энергия системы складывается из свободной dF и связанной TdS:

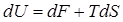. (8)

Сделав подстановку из уравнения (8) в (7), получим выражение для изменения свободной энергии системы

.

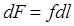При постоянных объеме и температуре образца

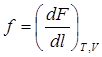. (9)

Выражение (9) раскрывает физический смысл деформирующей силы: она равна изменению свободной энергии системы в расчете на единицу удлинения. Таким образом, выражение для изменения свободной энергии (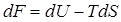) можно перевести в выражение для изменения термодинамических параметров эластомеров в процессе деформации:

,

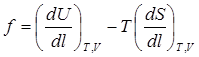или

.

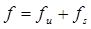Сила, приложенная к эластомеру, вызовет его деформацию, связанную с изменением внутренней энергии и энтропии.

Пространственно-сшитые эластомеры с малой частотой сшивок (редкосетчатые) при температурах, значительно превышающих температуру стеклования, ведут себя как идеальные эластомеры, в которых 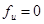. В идеальном эластомере возникающее напряжение обусловлено только изменением энтропии.

Очевидно, что при малой деформации идеально твердого тела (кристалла), когда кристаллическая структура не нарушается, напряжение возникает только за счет изменения межатомных расстояний кристаллической решетки, и тогда для идеального кристалла .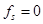

В пространственно-сшитых эластомерах при комнатной температуре изменение внутренней энергии ответственно лишь за 5 – 15% действующего напряжения. Вклад зависит от удлинения: при малых удлинениях, когда энтропия меняется незначительно, вклад внутренней энергии велик, однако в широком диапазоне удлинений величина действующего напряжения обусловлена главным образом изменением энтропии. Чем ближе температура к температуре стеклования, т.е. чем больше эластомер по свойствам напоминает пластмассу, тем больше роль энергетической составляющей 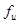, тем больше ее доля в величине общей силы (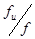). Это видно на примере пространственно-сшитого полигексилметакрилата (табл. 4). При 100°С полигексилметакрилат ведет себя как обычный эластомер, а при 30°С свойства его близки к свойствам пластмассы.

Таблица 4. Значения доли энергетической составляющей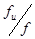

при разных температурах для полигексилметакрилата

T, °С
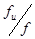
	0,97	0,65	0,41	0,26

Правильность выводов, сделанных на основе термодинамического рассмотрения процесса деформации эластомеров, подтверждается измерением сопутствующих тепловых эффектов.

Если стальной стержень с висящим на нем грузом нагреть, то стержень удлинится. Кроме обычного теплового расширения, проявится ослабление взаимодействия атомов в кристаллической решетке, и упругость стали, удерживающей груз, уменьшится. С эластомерами дело обстоит иначе. При деформации эластомеров вся работа внешних сил превращается в теплоту, а энтропия деформируемого эластомера уменьшается.

Явление выделения тепла при растяжении тесно связано с сокращением растянутого эластомера при нагревании. Если образец эластомера быстро растянуть, его температура повышается. Но если его держать в растянутом состоянии до тех пор, пока он остынет до комнатной температуры, а затем освободить концы, то это приведет к понижению температуры образца. Следовательно, выделение тепла обратимо.

Уменьшение энтропии при растяжении эластомера легко объяснимо исходя из природы эластической деформации. Растяжение эластомера, связанное с распрямлением скрученных макромолекул, приводит к уменьшению числа возможных конформаций.

Согласно формуле Больцмана

,

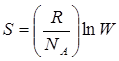где R – универсальная газовая постоянная, N_A – число Авогадро, W – термодинамическая вероятность состояния.

Термодинамическая вероятность состояния определяется числом микросостояний, которые соответствуют данному макросостоянию. Согласно формуле, с уменьшением W уменьшается энтропия. Таким образом, растяжение эластомера приводит к статистически менее вероятному термодинамическому состоянию, т.е. к уменьшению энтропии.

Дата добавления: 2014-01-03