Условные вероятности

При решении вероятностных задач часто приходится вычислять вероятность некоторого события А₁ при условии, что произошло другое событие А₂. Вероятность события А₁, вычисленная при условии, что произошло событие А₂, называется условной и обозначается через Р(А₁ / А₂), причем Р(А₁ / А₂)= Р(А₁А₂)/ Р(А₂), где Р(А₁А₂) - вероятность совместного осуществления событий А₁ и А₂, Р(А₂) - безусловная вероятность события А₂.

Событие А₁ называется статистически зависимым от события А₂, если вероятность события А₁ зависит от того, произошло или не произошло событие А₂. Математически условие зависимости события А₁ от А₂ записывается в виде Р(А₁ / А₂)¹ Р(А₁).

Отметим два обстоятельства. Во-первых, рассматриваемое событие может зависеть не только от одного, но и от нескольких событий (успешный радиообмен между корреспондентами зависит от исправности аппаратуры, интенсивности помех, условий распространения радиоволн и других факторов). Во-вторых, если событие А₂ благоприятствует событию А₁, то Р(А₁ / А₂)³ Р(А₁). Возможен и обратный характер зависимости. Пусть, например, событие А₁ означает факт обнаружения наземной радиолокационной станцией самолета противника, а событие А₂ - постановку этим самолетом помех наземной РЛС. В этом случае осуществление события А₂ снижает вероятность события А₁.

Если события А₁ и А₂ статистически независимы, то появление одного из них не влияет на вероятность появления другого. В этом случае Р(А₁ / А₂)= Р(А₁), т.е. условная вероятность события А₁ равна безусловной вероятности этого события. Независимость событии А₁ и А₂ являются взаимной, т.е. если Р(А₁ / А₂)= Р(А₁), то выполняется и другое равенство Р(А₂ / А₁)= Р(А₂). Кроме того, если независимы события А₁ и А₂, то независимы и противоположные им события 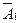и .

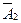Зависимость или независимость событий можно обычно установить без вычисления соответствующих вероятностей, исходя из существа рассматриваемого явления. Так, например, отказ аппаратуры наведения на одном командном пункте не зависит от такого же события на другом командном пункте, если командные пункты не имеют общего источника питания электроэнергией и если отсутствует какая-либо связь между условиями работы на них аппаратуры наведения.

Дата добавления: 2014-01-03