
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение прямых линий регрессии по выборочным данным
ЛЕКЦИЯ №3
Две СВ могут быть связаны либо функциональной зависимостью, либо быть независимыми, либо связаны зависимостью другого рода, называемой статистической (иначе стохастической).
Как правило, функциональная зависимость реализуется редко, так как одна или две СВ подвержены действию многих случайных факторов.
СВ независимы, если закон распределения одной из них не зависит от того, какие значения принимает другая СВ.
Статистической называется такая зависимость, при которой изменение одной из них влечет за собой изменение распределения другой. В частности, если при изменении одной из величин изменяется среднее значение (условное матожидание) другой, статистическую зависимость называют корреляционной.
Приведем примеры статистической зависимости:
1.Рост 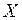 школьников и их возраст
школьников и их возраст 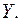
2.Количество удобрений 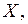 внесенных на
внесенных на 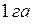 и урожай
и урожай 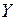 с этого участка.
с этого участка.
Пусть изучается система количественных признаков 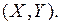 Допустим в результате
Допустим в результате 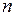 независимых опытов получены
независимых опытов получены 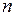 пар чисел
пар чисел 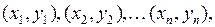 которые могут быть представлены в виде таблицы:
которые могут быть представлены в виде таблицы:
Таблица 1
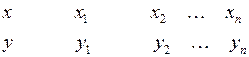
Рассмотрим случай, когда есть основания предполагать наличие линейной корреляционной зависимости между величинами 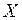 и
и 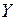 (в генеральной совокупности их значений) т.е. когда линейные уравнения регрессии имеют вид:
(в генеральной совокупности их значений) т.е. когда линейные уравнения регрессии имеют вид:
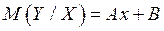 (1)
(1)
(1) –уравнение линейной регрессии 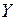 на
на 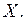
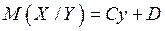 (2)
(2)
(2) –уравнение линейной регрессии 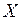 на
на 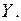
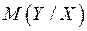 −условное матожидание
−условное матожидание 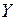 при конкретном
при конкретном 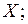
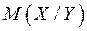 − условное матожидание
− условное матожидание 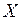 при конкретном
при конкретном 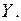
В этих случаях для описания корреляционных зависимостей между величинами 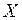 и
и 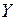 по результатам выборочных наблюдений вводят выборочные уравнения линейной регрессии
по результатам выборочных наблюдений вводят выборочные уравнения линейной регрессии 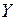 на
на 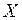 и
и 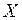 на
на 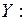
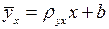 (3)
(3)
(3) –уравнение линейной регрессии 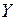 на
на 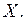
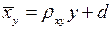 (4)
(4)
(4) –уравнение линейной регрессии 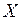 на
на 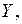
где 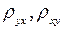 - выборочные коэффициенты линейной регрессии, имеющие смысл выборочных оценок коэффициентов
- выборочные коэффициенты линейной регрессии, имеющие смысл выборочных оценок коэффициентов 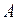 и
и 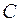 в формулах (1), (2). При этом
в формулах (1), (2). При этом 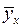 и
и 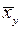 являются оценками условных математических ожиданий
являются оценками условных математических ожиданий 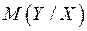 и
и 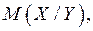 а параметры
а параметры 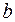 и
и 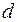 - оценками
- оценками 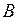 и
и 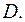
|
Дата добавления: 2014-01-03; Просмотров: 224; Нарушение авторских прав?; Мы поможем в написании вашей работы!