Передаточная функция

Связь между частотными и временными характеристиками

Передаточной функцией усилителя называется отношение преобразований Лапласа отклика y (t) и входной переменной x (t) при нулевых начальных условиях:

W (p) = Y (p)/ X (p).

В зависимости от удобств представления конкретного усилителя в качестве отклика y (t) может выбираться напряжение U _вых(t) или ток I _вых(t). Независимо от этого выбора в качестве входной переменной можно принять напряжение U _вх(t), или ток I _вх(t). При этом наряду с безразмерными передаточными функциями K_U (p) = U _вых(p)/ U _вх(p) и K_I (p) = I _вых(p)/ I _вх(p) существуют передаточные функции с размерностью проводимости (крутизны усиления), например S (p) = I _вых(p)/ U _вх(p), и с размерностью сопротивления, например Z (p) = U _вых(p)/ I _вх(p).

Наибольшее применение находят безразмерные передаточные функции K (p), характеризующие усиление по напряжению или по току.

Заменой переменной p на мнимую частоту j ω передаточная функция переводится в частотную форму, причем из выражения передаточной функции получаем выражение комплексного коэффициента усиления:

K (j ω) = [ K (p)] _{p = j ω}.

Приводя это выражение к виду произведения модуля на фазовый множитель K (j ω) = K (ω)e ^{jφ( ω)}, получим АЧХ и ФЧХ усилителя.

Обратно, если в результате анализа усилительной схемы найдено выражение комплексного коэффициента усиления K (j ω), то передаточная функция получается путем замены аргумента j ω комплексной переменной p:

K (p) = [ K (j ω)] _{j ω= p}.

Частотные и переходные искажения представляют собой линейные искажения, вызываемые одной и той же причиной (наличие в схеме усилителя реактивных элементов), но одни (частотные) проявляются в установившемся режиме, а другие – в переходном режиме работы усилителя.

Из теории электрических цепей известно, что связь между временной и частотной характеристиками линейной цепи устанавливается посредством интеграла Фурье и имеет в символической форме записи вид:

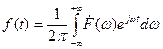
или

,

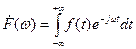в зависимости от того, какая из характеристик является заданной и какая – искомой. Здесь F (t) – непериодическая функция времени, описывающая переходной процесс в рассматриваемой цепи, F (ω) – соответствующая спектральная функция.

Спектральная функция F (ω) непериодической функция времени F (t) является, как известно, сплошной (непрерывной) и представляет собой частотную зависимость комплексной амплитуды бесконечно малого участка спектра шириной d ω около частоты ω.

Если под непериодической функцией времени F (t) понимать ПХ усилителя, то частотный спектр F (ω) должен соответствовать подведению ко входу усилителя единичной функции и учитывать искажающее воздействие на нее исследуемого усилителя.

Другими словами, необходимо, чтобы частотный спектр

F (ω) = F ₁(ω) F ₂(ω),

где F ₁(ω) – частотный спектр единичной функции, а F ₂(ω) – частотная характеристика усилителя, определяемая его коэффициентом передачи K (ω).

Известно, что F ₁(ω)=1/ j ω. Таким образом, выражение () может быть представлено в виде:

,

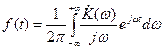определяющем зависимость между переходной F (t) и частотной K (ω) характеристиками усилителя.

Приведенная связь между характеристиками позволяет определить поведение усилителя в переходном режиме, если известна его частотная характеристика. Может быть показано, что крутизна переднего фронта ПХ возрастает (уменьшение t _ф) по мере расширения полосы равномерно усиливаемых частот, а протяженность плоской части этой характеристики, ограничиваемая допустимой величиной спада ∆ С, возрастает по мере расширения полосы равномерно усиливаемых низких частот диапазона. Другими словами, чем лучше частотная характеристика усилителя, тем более совершенной является его ПХ.

Из сказанного следует, что анализ и расчет усилителя могут производиться как в частотным, так и временным методом. В случае применения частотного метода целью расчета является получение требуемого усиления в заданном диапазоне частот при допустимых искажениях. При использовании временного метода целью расчета является получение требуемого усиления при допустимых переходных искажениях (длительность фронта, выбросы, подъем и спад плоской части характеристики).

В принципе оба метода равноценны. Однако очевидно, что при расчете усилителей непрерывных колебаний (аналоговых сигналов), работа которых частично или полностью относится к установившемуся режиму, удобнее пользоваться частотным методом, в то время как при расчете усилителей, сигналы которых представляют собой последовательность ряда кратковременных непериодических импульсов, удобнее применять временной метод. В случае необходимости всегда может быть осуществлен переход от одного метода анализа к другому.

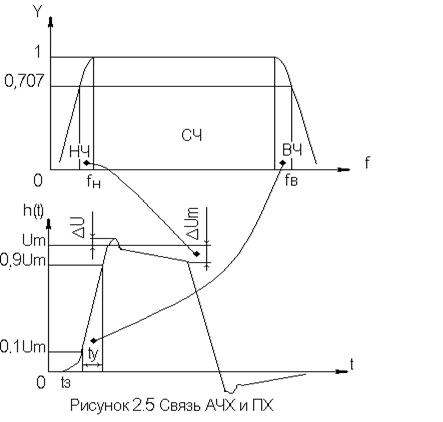АЧХ и ПХ отражают одни и те же физические процессы в различной форме (частотной и временной). Связь частотных и временных искажений иллюстрируется рис. 2.5.

Некоторые УУ (УПТ, ОУ и т.д.) могут характеризоваться другими специфическими показателями, которые будут рассмотрены по мере необходимости.

Дата добавления: 2014-01-03