Функции и их свойства

Переменной называют величину 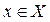, принимающую значения из некоторого множества значений Х.

Если каждому значению переменной х из множества Х поставлено в соответствие по определенному правилу f единственное значение переменной у из множества Y, то говорят, что задана функция 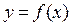, определенная на множестве Х с множеством значений Y. При этом используют следующие названия:

х ––– аргумент (независимая переменная);

у – значение функции (зависимая переменная);

Х – область определения функции (ООФ);

Y – множество значений функции (ОЗФ).

Функция 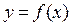, область определения Х которой симметрична относительно начала координат, называется четной, если 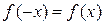, и называется нечетной, если , ".

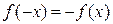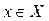Примеры. y = cos x – четная функция, y = x ³ – нечетная функция, 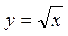– функция общего вида (ни четная, ни нечетная).

Функция 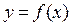называется периодической, если существует положительное число Т, такое, что , ".

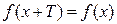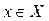Примеры. y = tg x – периодическая функция, наименьший период T = π, y = ln x – непериодическая функция.

Значение функции 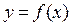– переменная величина, поэтому можно рассматравать новую функцию с аргументом у: z = g (y), где ,
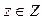т. е. функцию z = g (f (x)). Такая функция называется сложной функцией от х, или суперпозицией функций f и g.

Пример. z = tg(х ² + 3 x -1) – суперпозиция функций z = tg у и у = х ² + 3 x -1.

Если 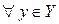ставится в соответствие единственное значение 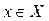, такое, что 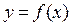, то говорят, что задана функция 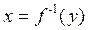, которую называют обратной по отношению к функции 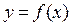. Функции f и 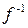называются взаимно обратными функциями. Если у обратной функции 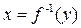обозначить аргумент буквой х, а функцию – буквой у, то графики взаимно обратных функци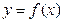й и 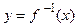будут симметричны относительно прямой у = х.

Пример. y = lg x и y = 10 ^x – взаимно обратные функции.

Все функции, задаваемые аналитическим способом, можно разбить на два класса: элементарные и неэлементарные. В классе элементарных функций выделяют основные элементарные функции: степенная (у = xⁿ), показательные (y = a^x), тригонометрические (y = sin x, y = cos x, y = tg x, y = ctg x), а также обратные к ним (логарифмические, обратные тригонометрические и др.). Элементарными называют функции, полученные из основных элементарных функций при помощи конечного числа операций сложения, вычитания, умножения, деления, а также суперпозиции основных элементарных функций. Все остальные функции относятся к неэлементарным.

Примеры. y = lg(cos x) – элементарная функция, т.к. является суперпозицией основных элементарных функций y = lg x и y = cos x; 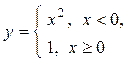– неэлементарная функция.

Нулями функции 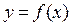называют точки х, в которых выполнено равенство 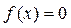. Нули функции – это абсциссы точек пересечения графика функции с осью Oх.

Пример. У функции y = lg(x) единственный нуль – точка х = 1.

Функция 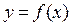называется монотонно возрастающей на интервале х Î(а; b), если для любых двух точек х ₁ и х ₂ этого интервала из неравенства х ₂ > х ₁ следует неравенство 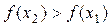, то есть если любому большему значению аргумента из этого интервала соответствует большее значение функции.

Функция 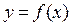называется монотонно убывающей на интервале х Î(а; b), если для любых двух точек х ₁ и х ₂ этого интервала из неравенства х ₂ > х ₁ следует неравенство .

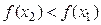Промежутки возрастания и убывания функции называются промежутками монотонности функции.

Если функция 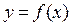монотонна на интервале хÎ (а; b), то она имеет обратную функцию .

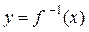Пример. Функция y = tg x монотонна на интервале 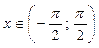, ее ОЗФ: 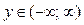. Она имеет обратную функцию y = arctg x, определенную на интервале 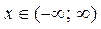, с ОЗФ: .

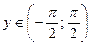Точка х ₀ называется точкой максимума функции 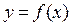, если существует такая двухсторонняя окрестность точки х ₀, что для всякой точки х ¹ х ₀ этой окрестности выполняется неравенство 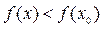. При этом число 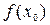называется максимумом функции 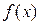и обозначается y _max.

Аналогично, если для всякой точки х ¹ х ₀ из некоторой окрестности точки х ₀ выполняется неравенство 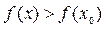, то х ₀ называется точкой минимума, а число 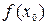– минимумом функции 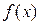и обозначается y _min.

Точки максимумов и минимумов называются точками экстремумов функции, а числа y _max и y _min называются экстремумами функции.

Пример. Функция y = cos x имеет точки максимумов 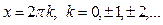, , 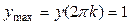и точки минимумов , .

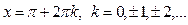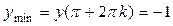Дата добавления: 2014-01-03