Линейная одномерная регрессионная модель

Пусть в результате эксперимента получена таблица некоторой зависимости

Таблица 2.1

			…
			…

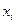
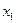
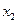
Результаты наблюдений отобразим на графике (см. рис. 2.2). Всего на графике n экспериментальных точек, которые соответствуют n наблюдениям.

а) Исследователь вносит гипотезу о структуре ящика

Предположим, что полученные данные (табл.2.1) подчиняются линейной гипотезе, то есть выход y зависит от входа x линейно, то есть гипотеза имеет вид: .

Данная модель называется линейной одномерной регрессионной моделью т.е модель, имеющая один вход и один выход.

Рис. 2.1. Одномерная модель черного ящика

б) Определение неизвестных коэффициентов a ₀ и a ₁ модели

Для каждой из n снятых экспериментально точек вычислим ошибку (невязку) между экспериментальным значением () и теоретическим значением (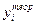), лежащим на гипотетической прямой (см. рис.2.2):

Рис. 2.2. Графический вид представления результатов
наблюдения над черным ящиком

Чтобы положительные ошибки не компенсировали в сумме отрицательные, каждую из ошибок возводят в квадрат и складывают их значения в суммарную ошибку s уже одного знака:

Цель метода — минимизация суммарной ошибки F за счет подбора коэффициентов . Другими словами, это означает, что необходимо найти такие коэффициенты линейной функции, чтобы ее график проходил как можно ближе одновременно ко всем экспериментальным точкам. Данный метод называется методом наименьших квадратов.

(2.5)

Суммарная ошибка F является функцией двух переменных 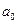и , то есть , меняя которые, можно влиять на величину суммарной ошибки (см. рис. 2.3).

Рис. 2.3. Примерный вид функции ошибки

Чтобы суммарную ошибку минимизировать, найдем частные производные от функции F по каждой переменной и приравняем их к нулю (условие экстремума):

(2.6)

Уравнения (2.6) можно переписать в виде так называемых нормальных уравнений:

(2.7)

Решив эту систему относительно переменных 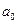и , получим конкретный вид искомой функции .

Для проверки точности оценок и адекватности модели используются критерии Стьюдента и Фишера.

в) Проверка

Естественно ожидать, что значения найденной функции в точках будут отличаться от табличных значений. Чтобы определить, принимается гипотеза или нет, нужно, во-первых, рассчитать ошибку между точками заданной экспериментальной и полученной теоретической зависимости и суммарную ошибку:

И, во-вторых, необходимо найти значение σ по формуле , где F - суммарная ошибка, n - общее число экспериментальных точек.

Если в полосу, ограниченную линиями и (рис. 2.4), попадает 68.26% и более экспериментальных точек , то выдвинутая нами гипотеза принимается. В противном случае выбирают более сложную гипотезу или проверяют исходные данные. Если требуется большая уверенность в результате, то используют дополнительное условие: в полосу, ограниченную линиямии , должны попасть 95.44% и более экспериментальных точек .

Рис. 2.4. Исследование допустимости принятия гипотезы

Расстояние S связано с σ следующим соотношением:

S = σ /sin(β) = σ /sin(90° – arctg(a ₁)) = σ /cos(arctg(a ₁)),

что проиллюстрировано на рис. 2.5.

Рис. 2.5. Связь значений σ и S

Условие принятия гипотезы выведено из нормального закона распределения случайных ошибок (см. рис. 2.6). P — вероятность распределения нормальной ошибки.

Рис. 2.6. Пределы отклонения экспериментальных

Дата добавления: 2014-01-03