Воздухораспределение в простом диагональном соединении

Рассмотрим методы определения воздушных потоков в ветвях простого диагонального соединения. Пусть воздух движется в диагонали от узла 2 к узлу 3. Тогда согласно второму закону сетей для контуров 1-2-3-1 и 2-4-3-2 (рис.6.13) можно записать следующие уравнения депрессии

R₁ (q₃+q₅)²+R₅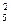*q-R₂ q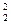=0 (6.53)

R₃ q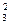-R₄*(q₂+q₅)²-R₅ q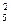=0 (6.54)

Уравнения (6.53) (6.54) содержат три неизвестных q₂, q₃, q₅. Разделим оба уравнения на R₅ q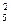и обозначим для сокращения записей

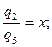
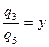
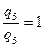(6.55)

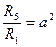
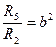
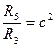
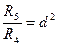(6.56)

С учетом принятых обозначений равенства (6.53) (6.54) будут иметь вид

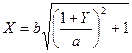(6.57)

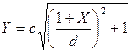(6.58)

Из уравнений (6.57) (6.58) необходимо определить значения X и Y. После этого решение продолжается в зависимости оттого, что задано Q или Н.

Если задан общий поток воздуха, то потоки воздуха в ветвях определяются следующим образом. Сложив, левые и правые части равенств (6.55) получим

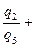
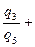
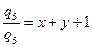(6.59)

Для случая, когда воздух движется в диагонали от узла 2 к узлу 3 q₂+q₃+q₅=Q тогда из равенства (6.59) получим

q₅=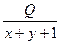 (6.60),

а из соотношений (6.55) определяем

q₂=q₅*x (4.61) q₃=q₅*y (6.62)

Потоки воздуха в ветвях R₁ и R₄ определяем, используя первый закон сетей

q₁=q₃+q₅ (6.63) q₄=q₂+q₅ (6.64)

Если задана общая депрессия соединения Н, то для определения общего потока и потоков воздуха в ветвях необходимо, прежде всего, определить общее сопротивление диагонального соединения. Это можно сделать на основе использования свойства последовательного соединения горных выработок, согласно которому общую депрессию диагонального соединения можно выразить как сумму депрессии последовательно соединенных ветвей, т.е.

Н_1-4=h_1-2+h_2-4 (6.65)

Н_1-4=h_1-3+h_3-4 (6.66)

H_1-4=h_1-2+h_2-3+h_3-4 (6.67)

H_1-4=h_1-3 -h_2-3+h_2-4 (6.68)

Любое из равенств (6.65-6.68) может быть использовано для расчета общего сопротивления диагонального соединения. Воспользуемся равенством (6.65). Выразим депрессии в этом равенстве через сопротивления и потоки воздуха

R₀ Q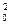=R₁ (q₃+q₅)²+R₃ q 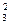(6.69)

Так как Q₀=q₂+q₃+q₅ равенство (4.69) будет иметь вид

R₀ (q₂+q₃+q₅)²= R₁ (q₃+q₅)²+R₃ q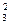 (6.70)

Разделив равенство (6.70) на q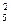получим

R₀ (x+y+1)²=R₁ (1+y)²+R₃ y² (6.71)

Из равенства (4.71) определяем общее сопротивление диагонального соединения

R₀=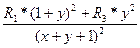 (6.72)

Определив R₀, подсчитываем общий расход воздуха в сети как:

Q₀=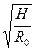 (6.73)

Дальнейшее решение задачи уже известно.

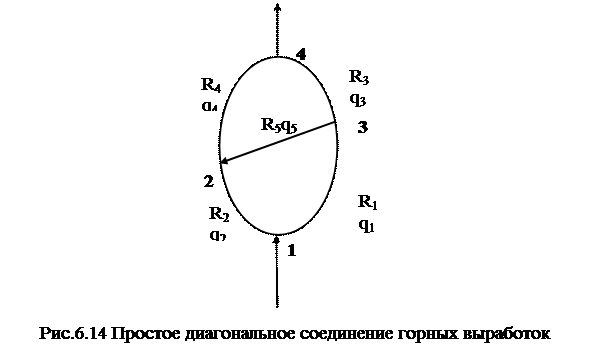
Все формулы данного подраздела справедливы только при той нумерации ветвей соединения, какая принята на рис.6.13. Если при определении направления потока в диагонали окажется, что он следует от узла 3 к узлу 2 (справа налево), то, чтобы не менять расчетных формул, нужно повернуть чертеж на 180⁰ относительно продольной оси и обозначить номера ветвей так, как это показано на рис.6.14

Таким образом, после определения значений X и Y из системы уравнений (6.57), (6.58) расчет распределения воздуха в простом диагональном соединении выполняется по элементарным формулам.

Рассмотрим способы решения этой системы. Мы имеем два квадратных уравнения, которые всегда могут быть сведены к одному уравнению 4-й степени, точное решение которого в радикалах возможно, но чрезвычайно громоздко и трудоемко. Поэтому в данном случае предпочтительнее приближенное решение. В литературе известно два довольно простых способа приближенного решения, примерно равных по трудности и точности:

1-спосорб последовательных приближений;

2-графический способ.

Дата добавления: 2014-01-03