Определение ошибок выборки

Итогом выборочного наблюдения является расчет обобщающих статистических характеристик (среднего значения, дисперсии и т.п.). Разность между показателями в выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности. Ошибки регистрации возникают из-за неправильных или неточных сведений. Источниками ошибок могут быть непонимание существа вопроса, невнимательность регистратора, пропуск или повторный счет некоторых единиц совокупности, описки при заполнении формуляров и т.д. Среди ошибок регистрации выделяются систематические, обусловленные причинами, действующими в каком-то одном направлении и искажающими результаты работы (например, округление цифр, тяготение к полным пятеркам, десяткам, сотням и т.д.), и случайные, проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.

Ошибки репрезентативности также могут быть систематическими и случайными. Систематические ошибки репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки – принцип случайности. Случайные ошибки репрезентативности означают, что, несмотря на принцип случайности отбора единиц, все же имеются расхождения между характеристиками выборочной и генеральной совокупности. Изучение и измерение случайных ошибок репрезентативности и является основной задачей выборочного метода.

Отличие выборочных и генеральных характеристик рассмотрим на условном примере. Известно, что в генеральной совокупности 1000 студентов средний балл успеваемости равен 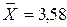. Далее были проведены две 10 % выборки. Обнаружилось что по первой выборке средний балл 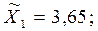по второй выборке средний балл .

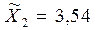Разность между показателями выборочной и генеральной совокупности и будет случайной ошибкой репрезентативности. Ошибки репрезентативности:

для первой выборки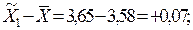

для второй выборки .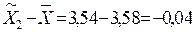

Если известно, что доля студентов, получивших оценки «4» и «5», составляет

по генеральной совокупности p = 0,60 или 60 %,

по первой выборке W₁ = 0,64, или 64 %,

по второй выборке W₂ = 0,59, или 59 %, то ошибки репрезентативности окажутся W ₁ -p = 0,64 – 0,6 = + 0,04;

W ₂ -p = 0,59 – 0,6 = – 0,01.

Как видно из расчетов, выборочная средняя и выборочная доля являются величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку. Размер их отклонения от генеральных значений случаен и оценивается посредством так называемой средней и предельной ошибки выборки. Средняя ошибка выборки (μ) определяется как среднее квадратическое отклонению показателя, деленное на квадратный корень из численности выборки. Величина среднего квадратического отклонения оценивается опять-таки по результатам проведенного выборочного наблюдения:

для средней величины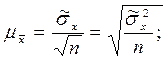 для доли .

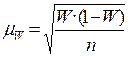При бесповторном отборе подкоренное выражение умножается на величину (1 –n/N), которая всегда меньше единицы. Поэтому величина средней ошибки выборки при бесповторном отборе оказывается меньшей, чем при повторном. В тех случаях, когда доля выборки незначительна и множитель (1 –n/N) близок к единице, поправкой можно пренебречь.

Понятие предельной ошибкой выборки связано с гарантирующим ее уровнем вероятности. Уровень вероятности задается через нормированное отклонения t, и наоборот. Значения t даются в таблицах нормального распределения вероятностей. Чаще всего используют следующие сочетания:

t	P
	0,683
1,5	0,866
2,0	0,954
2,5	0,988
3,0	0,997
3,5	0,999

Так, если t = 1, то с вероятностью 0,683 можно утверждать, что разность между выборочными и генеральными показателями не превысит одной средней ошибки. Предельные ошибки выборки 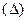определяются по формулам табл. 6.1. Размер предельной ошибки 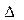зависит от: вариации признака (прямая связь), численности выборки (обратная связь), доверительной вероятности (прямая связь), метода отбора. На основе предельных ошибок, находят доверительные интервалы для генеральных показателей. Для 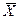это 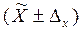. Для Р это 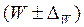. Значения t, а, следовательно, и Δ определяются природой изучаемого явления. Увеличение степени достоверности результатов требует большего значения t, т.е. увеличивает предельную ошибку. Менее достоверные результаты получаются при небольших предельных ошибках.

Таблица 6.1

Метод отбора	Предельные ошибки индивидуального отбора
для средней	для доли
Повторный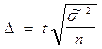
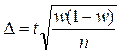
Бесповторный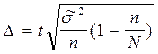

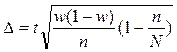
При стратифицированном отборе в выборку обязательно попадают представители всех групп и обычно в тех же пропорциях, что и в генеральной совокупности. Поэтому ошибка выборки в данном случае зависит главным образом от средней из групповых дисперсий 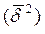. По правилу сложения дисперсий 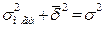, т.е. ошибка выборки для стратифицированного отбора всегда будет меньше, чем для собственно случайного.

При серийном (гнездовом) отборе мерой колеблемости будет межгрупповая дисперсия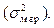

Дата добавления: 2014-01-03