Проверка ряда на наличие тренда

Ряд динамики теоретически может быть представлен в виде составляющих:

1) тренд – основная тенденция развития динамического ряда (к увеличению либо снижению его уровней);

2) циклические (периодические) колебания, в том числе сезонные;

3) случайные колебания.

Исследование тренда включает два основных этапа:

1) проверяется наличие тренда;

2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией (прогнозированием) результатов развития.

Проверка ряда на наличие тренда может выполняться несколькими методами.

1. Метод средних. Изучаемый ряд динамики разбивается на несколько интервалов (обычно на два), для каждого из которых определяется средняя величина. Выдвигается гипотеза о существенном различии средних. Если эта гипотеза принимается, то признается наличие тренда. В более мощном критерии Кокса и Стюарта весь анализируемый ряд динамики разбивают на три группы и сравнивают между собой уровни первой и последней групп.

2. Метод серий. По этому способу каждый конкретный уровень временного ряда считается принадлежащим к одному из двух типов: например, если уровень ряда меньше медианного значения, то считается, что он имеет тип А, в противном случае – тип В.

Теперь уровни временного ряда выступают как последовательность типов. В образовавшейся последовательности типов определяется число серий. Серией называется любая последовательность элементов одинакового типа, граничащая с элементами другого типа.

Так, временной ряд уровней брачности (см. ниже) имеет после упорядочения по возрастанию на 7-м месте значение 9,9 и на 8-м месте – значение 10,4. Отсюда медиана ряда равна (9,9+10,4):2=10,15. Ряд типов выглядит как ВВВВВВВААААААА. В данном примере число серий R= 2.

Для приведенного ниже ряда объемов продаж акций по месяцам имеем последовательность типов ААВВВАААВBAB. Для данного ряда R = 6.

Если во временном ряду общая тенденция к росту или снижению отсутствует, то количество серий является случайной величиной, распределенной приближенно по нормальному закону (для n>10). Следовательно, если закономерности в изменениях уровней нет, то случайная величина R оказывается в доверительном интервале

.

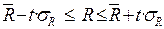Параметр t назначается в соответствии с принятым уровнем доверительной вероятности Р. Например, для нормального распределения

Р	0,683	0,950	0,954	0,990	0,997
t		1,960		2,576

Среднее число серий: .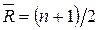

Среднее квадратическое отклонение числа серий: .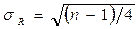

Здесь n – число уровней ряда.

Выражение для доверительного интервала приобретает вид

.

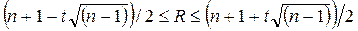Полученные границы доверительного интервала округляют до целых чисел, уменьшая нижнюю границу и увеличивая верхнюю.

В нашем примере (для Р = 0,954) имеем:

ряд уровней брачности: 3 £ R £ 12;

ряд объема продаж акций: 3 £ R £ 10.

Как видно, для ряда динамики брачности показатель числа серий R = 2 выходит за пределы возможного случайного поведения и, следовательно, в изменении уровней ряда имеется общая закономерность, тенденция. Напротив, для ряда объемов продажи акций число серий R = 6, что вполне (с Р = 0,954) укладывается в пределах случайного поведения, и гипотеза о наличии общей закономерности снижения или возрастания объемов продаж во времени не может быть принята (с вероятностью ошибки 0,046).

3. Графический метод. Для подтверждения наличия или отсутствия тренда часто достаточно представить уровни временного ряда на графике (см. тему «Статистические графики»). Графическая иллюстрация развития во времени считается достаточно убедительной.

Непосредственное выделение тренда может быть выполнено тремя методами.

1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету средних уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).

2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Количество уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5, 7 и т.д. точек) или четным (2, 4, 6 и т.д. точек). При нечетном сглаживании каждое полученное среднее арифметическое значение закрепляют за серединой интервала. При обработке ряда четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только по 50 %; полученное среднее арифметическое значение также закрепляют за серединой каждого расчетного интервала. Последовательно передвигая интервал сглаживания получают последовательность средних (скользящих) значений.

Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда. Если необходимо, то их получают специальными приемами. Так, при сглаживании по трем точкам выровненное значение в начале ряда рассчитывается по формуле

.

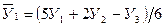Для последней точки расчет симметричен.

При сглаживании по пяти точкам имеем:

,

.

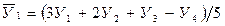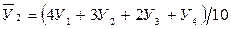Для последних двух точек ряда расчет сглаженных значений полностью симметричен сглаживанию в двух начальных точках.

3. Аналитическое выравнивание. Под этим понимается определение аналитического выражения, формулы – f(t) для основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает как бы в зависимости только от течения времени t. Отклонения конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически.

Трендовая модель имеет вид

У_t = f(t) + e_t,

где f(t) – уровень, определяемый тенденцией развития (трендовая составляющая); e_t – случайное и циклическое отклонение от тенденции.

В процессе аналитического выравнивания определяется конкретный вид и параметры аналитической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.

Обычно при выравнивании ряда используются следующие зависимости:

линейная f(t) = a₀ + a ₁· t;

параболическая f(t) = a₀ + a ₁ ·t + a ₂ ·t²,

экспоненциальные f(t) = exp (a₀ + a ₁ ·t)
или f(t) = ехр (а₀ + a ₁ ·t + a ₂· t ² ).

Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.

Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.

Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т.п.).

В большинстве случаев для оценка параметров (а ₀, а ₁, а ₂,...) используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выровненных:

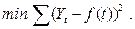
Для линейной зависимости f(t)=a₀+ a ₁· t; параметр a ₀ рассматривают как обобщенный начальный уровень ряда; а ₁– параметр, показывающий, на сколько изменится результат при изменении времени на единицу. Таким образом, а ₁ можно представить как теоретический средний абсолютный прирост.

Оценку надежности полученного уравнения выполняют через критерий (F). Определяется фактический уровень (F_факт) –

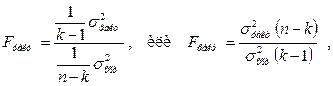
который сравнивается с теоретическим (табличным) значением. Здесь k – число параметров уравнения тенденции; n – число уровней ряда. В расчете участвуют показатели факторной и остаточной дисперсий. Факторная дисперсия 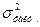оценивает вариацию теоретических, полученных по уравнению тренда уровней ряда динамики относительно общего среднего значения этого ряда. Остаточная дисперсия 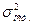оценивает вариацию теоретических, полученных по уравнению тренда уровней ряда динамики относительно их фактических значений. Общая дисперсия ряда динамики состоит из факторной и остаточной дисперсий.

Табличное (теоретическое) значение F -статистики находится при n₁=(k –1), n₂=(n-k) степенях свободы и уровне значимости α (обычно α=0,05). Если F_факт>F_теор, то уравнение тренда признается статистически значимым; построенная модель адекватна фактической временной тенденции.

В качестве примера рассмотрим число зарегистрированных браков на 1000 жителей России за период с 1977 по 1990 г.

Год	Число зарегистрированных браков,
	11,2
	10,9
	10,7
	10,6
	10,6
	10,4
	10,4
	9,6
	9,7
	9,8
	9,9
	9,5
	9,4
	9,1

Для определения параметров линейной трендовой модели (а ₀ и а ₁)следует решить систему из двух уравнений:

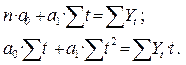
В этой системе нумерация уровней может быть принята либо естественной (1977, 1978 и т.д.), что не очень удобно для вычислений, особенно ручных, либо взята условной – от 1 до 14[12]. Решение системы дает параметры: а ₀ =11,22308; а ₁ = –0,14593. Таким образом, уравнение линейной тенденции имеет вид;

Y _t = 11,22308 – 0,14593· t; где t = 1, 2, …, 14.

Параметры полученного уравнения можно интерпретировать следующим образом: а ₀ = 11,223 – это исходный уровень брачности по России за период до 1977 г.; а ₁ = –0,146 – показывает, что в России за период с 1977 по 1990 г. происходило снижение уровня брачности на 0,146 %о ежегодно.

На графике (рисунок 8.1) видно, что в 1977÷90 гг. отчетливо наблюдалась общая тенденция снижения уровня брачности. Статическая проверка подтверждает значимость линейного тренда: фактическое значение F -статистики равно 137,265. Табличное значение F -статистики F _теор=4,747 при значимости a=0,05 и степенях свободы n₁=(k–1)=1; n₂=(n–k)=12 (F_теор=9,330 при a=0,01, n₁=1, n₂=12). Коэффициент линейной корреляции равен 0,95896, что убедительно подтверждает адекватность полученного уравнения линейной тенденции данного ряда динамики.

Дата добавления: 2014-01-03