Анализ взаимосвязанных рядов динамики

Под взаимосвязанными рядами динамики понимают такие, в которых уровни одного ряда в какой-то степени определяют уровни другого. Например, ряд, отражающий внесение удобрений на 1 га, связан с временным рядом урожайности; ряд уровней средней выработки связан с рядом динамики средней заработной платы; ряд среднегодового поголовья молочного стада определяет годовые надои молока и т.д. В простейших случаях анализа исчисляют коэффициенты опережения по темпам роста или прироста.

Коэффициенты опережения по темпам роста – это отношение темпов роста (цепных или базисных) одного ряда к соответствующим по времени темпам роста (также цепным или базисным) другого ряда. Аналогично находятся и коэффициенты опережения по темпам прироста.

Анализ взаимосвязанных рядов – одна из наиболее сложных задач при изучении временных последовательностей. Нередко совпадение общих тенденций развития объясняется не взаимной связью, а прочими не учитываемыми факторами. Поэтому в сопоставляемых рядах предварительно избавляются от влияния существующих в них тенденций, после чего проводится анализ взаимосвязи по отклонениям от тренда.

Отклонения проверяются и на наличие автокорреляции. Под автокорреляцией понимается зависимость последующих уровней ряда от предыдущих. Для проверки наличия автокорреляции используется критерий Дарбина-Уотсона:

,

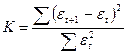где e_t – отклонение фактического уровня ряда в точке t от теоретического (выровненного) значения. При К =0 имеется полная положительная автокорреляция, при К =2 автокорреляция отсутствует, при К =4 – полная отрицательная автокорреляция. Если в отклонениях от тенденции подтверждается наличие автокорреляции (положительной или отрицательной), её исключают. Это можно сделать тремя способами.

1. Для каждого из взаимосвязанных рядов динамики Х и Y получают уравнение тренда и рассчитывают отклонения:

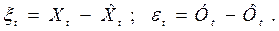
Для каждой последовательности (x_t) и (e_t) выполняется проверка на автокорреляцию по критерию Дарбина-Уотсона. Если значение К близко к 2, то данный ряд отклонений оставляют без изменений. Если же К заметно отличается от 2, то находят параметры уравнения авторегрессии[13].

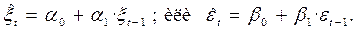
Подсчитываются новые остатки: 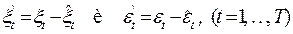и, в заключение, коэффициент корреляции признаков X и Y:

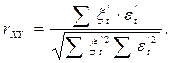
2. Корреляция первых разностей. От исходных рядов динамики Х и Y переходят к новым, построенным по первым разностям:

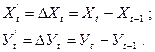
По DХ и DУ определяют направление и силу связи в регрессии:

DУ = f(DX) = С ₀ + С ₁· DХ.

3. Включение времени в уравнение связи. У_t = f(X_t, t). В простейших случаях уравнение выглядит следующим образом:

Y _t = а ₀ + а ₁ ·X _t + a ₂ ∙t.

Контрольные вопросы

1. Понятие ряда динамики, основные элементы, классификация

2. Правила построения рядов динамики

3. Основные показатели анализа рядов динамики

4. Структура временного ряда

5. Способы проверки ряда динамики на наличие тренда

6. Методы определения тенденции временного ряда

7. Аналитическое выравнивание, основные этапы

8. Методы исследования сезонных колебаний в рядах динамики

9. Понятие связного анализа, автокорреляция, методы ее исключения

ТЕМА 9. ИНДЕКСЫ·

9.1. Индивидуальные индексы и их применение в экономическом анализе

9.2. Общие индексы и их применение

9.3. Общий индекс как средняя величина индивидуальных индексов

9.4. Индексный метод анализа итогового показателя и структурных изменений

9.5. Индексы средних величин

9.6. Территориальные индексы

9.1. Индивидуальные индексы и их применение
в экономическом анализе

Индекс – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Условия могут различаться во времени (индексы динамики), в пространстве {территориальные индексы}, в выборе в качестве базы сравнения какого-либо условного уровня, например планового показателя, уровня договорных обязательств (индекс выполнения обязательств, индекс планового задания). В экономическом анализе индексы используются не только для сопоставления уровней изучаемого явления, но и для оценки значимости причин, объясняющих абсолютное различие сравниваемых уровней.

Относительная величина, получаемая при сравнении уровней, называется индивидуальным индексом, если исследователь не интересуется структурой изучаемого явления и количественную оценку уровня в данных условиях сравнивает с конкретной величиной уровня этого явления в других условиях. Так, сумма выручки от продажи товара в условиях отчетного года Q ₁ сравнивается с аналогичной суммой выручки базисного года Q ₂. В итоге получаем индивидуальный индекс товарооборота

i_o = Q₁/Q₂.

Индивидуальные индексы можно рассчитать для любого интересующего нас показателя, если он имеет количественное выражение. В частности, сумма выручки определяется ценой товара (р) и количеством продаж в натуральном измерении (q). Можно определить индивидуальные индексы цены i_p и количества проданных товаров i_q:

i_p = p ₁ /p ₀, i_q = q ₁ /q ₀.

С аналитической стороны i_q показывает, во сколько раз увеличилась (или уменьшилась) общая сумма выручки под влиянием изменения объема продажи в натуральных единицах. Аналогично i_p показывает, во сколько раз изменилась общая сумма выручки под влиянием изменения цены товара. Очевидно, что

i_Q = i_q·i_p или Q ₁ = Q ₀ ·i_q·i_p.

Вторая формула представляет двухфакторную индексную мультипликативную модель итогового показателя, в данном случае – объема товарооборота. Посредством такой модели находят прирост итога под влиянием каждого фактора в отдельности. Так, если выручка от продажи некоторого товара возросла с 8 млн. руб. в предыдущем периоде до 12,180 млн. руб. в последующем и известно, что это объясняется увеличением количества проданного товара на 5 % при цене на 45 % большей, чем в предыдущем периоде, то имеет место соотношение:

12,180=8·1,05·1,45 млн. руб.

Очевидно, что общий прирост выручки в сумме 12,180-8 = 4,180 млн. руб. объясняется изменением объема продажи и цены. Прирост выручки за счет изменения объема продажи (в натуральном выражении) составит

DQ(q) = Q₀ · (i_q - 1 ),

или в нашем примере DQ(q) = 8∙(1,05 - 1) =+0,40 млн. руб.

Тогда за счет изменения цены данного товара сумма выручки изменилась на

DQ(p) = (Q ₁ –Q ₀) –DQ(q) = Q ₁ –Q ₀ ∙i_q = Q₀∙i_q·(i_p– 1 ),

или DQ(p) =8∙1,05∙(1,45 - 1) = +3,78 млн. руб.,

(проверка: 3,780 + 0,400 = 4,180).

Возможен другой способ распределения общего прироста по факторам в двухфакторной индексной мультипликативной модели, а именно:

DQ(q) = Q₀∙i_p∙(i_q- 1 ) и DQ(p) = Q₀ ∙(i_p –1 ).

Прирост выручки (4,18 млн руб.) объясняется теперь: ∙

изменением цены DQ(p) = 8∙(1,45 - 1)=3,60 млн. руб.,

изменением объема продажи DQ(q) = 8∙1,45∙(1,05 - 1) = 0,58 млн. руб.

Выбор конкретной формы разложения общего прироста итога должен определяться конкретными условиями развития изучаемого показателя, в данном случае – конъюнктурой спроса-предложения. На практике и в большинстве научных рекомендаций в настоящее время преобладает первое направление, когда сначала выясняют вклад в общий прирост количественного фактора (q) при базисном уровне качественного признака (p), а затем – вклад качественного фактора (цены) в расчете на отчетный уровень количественного показателя.

Дата добавления: 2014-01-03