Стадия замедленного разряда — ионизации

Если самой медленной стадией электрохимического процесса является переход заряженных частиц через границу раздела фаз, то имеет место замедленная стадия разряда — ионизация.

Теория, описывающая кинетические закономерности переноса заряда через границу раздела фаз, называется теорией замедленного разряда. Впервые в качественной форме она была сформулирована М. Фольмером и А.Н. Фрумкиным.

Основная причина влияния скачка потенциала на скорость элек­трохимических реакций заключается в том, что скорость таких реак­ций лимитируется стадией переноса заряда, энергия активации ко­торого является функцией потенциала на границе металл-раствор.

DG^# _a,k - энергия активации процесса окисления, восстановления.

Уравнение Аррениуса

Скорость процесса окисления

i_a = a_ox n_a F K_ox exp(-DG^# _a/RT)

Скорость процесса восстановления

i_k = a_red n_k F K_red exp(-DG^# _k/RT)

При равновесном потенциале E ₀ DG=0. DG^#_a = DG^#_k= DG^#

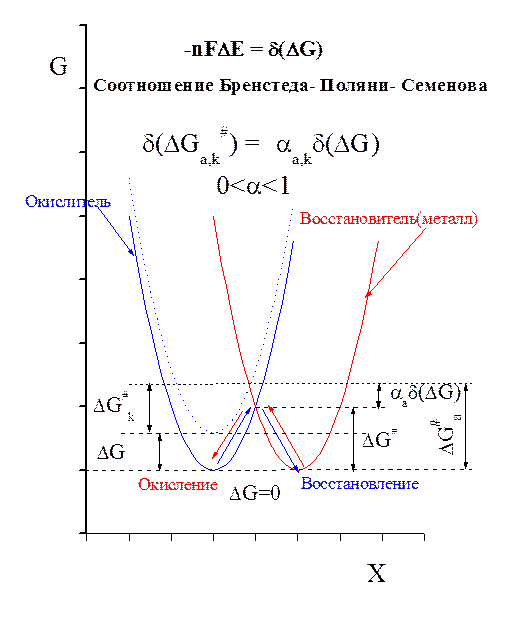DG_a = DG_k = DG = -nFDE

d(DG) = DG

Катодный процесс

DG + DG^#_k = DG^# + a_aDG; DG^#_k - DG^# = -a_kDG = a_knFDE;

DG^#_k = DG^# + a_knFDE

Анодный процесс

DG^#_a = DG^# + a_aDG; DG^#_a = DG^# - a_knFDE

DG = DG^#_a- DG^#_k = -(a_a + a_k)nFDE = -nFDE, но поскольку
DG = -nFDE, то a_a + a_k =1

Принято обозначать a_a как b а a_k – как a.

Для реакции

Me → Meⁿ⁺ + ne

Справедливо уравнение Фольмера-Фрумкина.

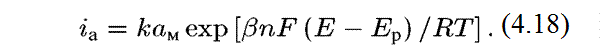
Для простейшего случая протекания процесса в одну стадию, т.е. при одновременном отщеплении n элек­тронов, это уравнение имеет вид:

Здесь i_а — скорость анодной реакции, выраженная в единицах плот­ности тока; а — активность реагента (в данном случае — металла); β — коэффициент переноса для анодной реакции, Ε — электродный потенциал металла в данных условиях; Е_р — равновесный элек­тродный потенциал реакции (4.1).

Таким образом, скорость электрохимической реакции зависит от потенциала, изменяясь по экспоненциальному закону. Это — особен­ность любого электрохимического процесса, в том числе и процесса растворения металла. Для последнего случая следует учитывать, что

активность металла (a _Μ), как правило — величина постоянная, так что уравнение (4.18) следует переписать в виде:

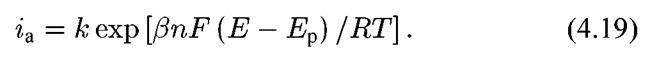
В форме, наиболее удобной для практического использования, уравнение (4.19) целесообразно прологарифмировать:

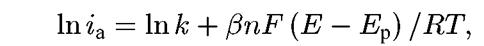
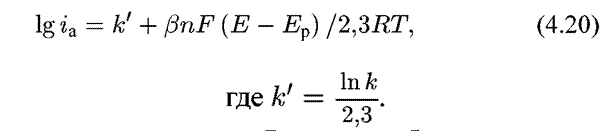или после перевода натуральных логарифмов в десятичные:

Введение обозначения:

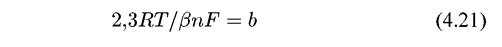приводит к уравнению

где а' — постоянная, а

— характеристика скорости растворения металла.

Поскольку закон, лежащий в основе зависимости i_а от Е, выра­жающейся уравнением (4.22), был сформулирован ученым Тафелем, уравнение это называется уравнением Тафеля. Величину b соответ­ственно называют тафелевым наклоном (имея ввиду наклон линей­ных кривых в координатах Ε — lg i_a, широко используемых при ре­шении научных и прикладных задач, связанных с исследованием электрохимического растворения металлов).

Понятие «наклон» означает, что при изменении плотности тока в 10 раз, что эквивалентно изменению логарифма этой величины на единицу, потенциал электрода, выраженный в мВ, изменяется на величину b.

Величина наклона b является важной характеристикой и в ряде случаев служит аргументом для заключений о кинетике электрохи­мических реакций.

Например, наклон поляризационных кривых в координатах Ε — lg i позволяет сделать заключение о числе электронов, участвующих в реакции. Рассмотрим случай, когда происходит раство­рение металла в одну стадию:

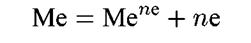
Предположим, что металл может переходить в раствор как в фор­ме одновалентных Ме⁺, так и двухвалентных Ме²⁺ катионов. В любом случае для описания скорости реакции применимо урав­нение (4.22), где наклон b = 2,3RT/bnF. Поскольку, как правило, β ~ 0,5, то при температуре 20 °С при подстановке численных значений констант R и F получаем:

для случая n = 1 величина b = 118 мВ;

для случая n = 2 величина b = 59 мВ.

Поляризационная кривая в общем случае имеет вид, изображенный на рис. 4.6 в коорди­натах Ε — lgi.

Участок АВ отвечает малому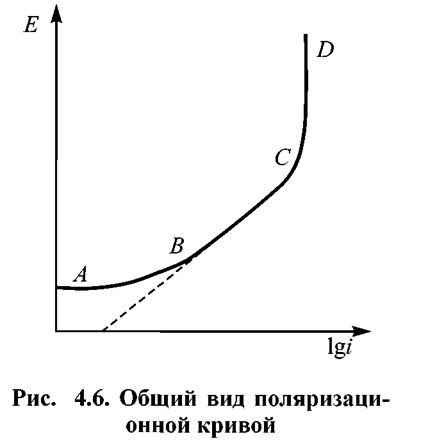
значению поляризации. Следует учитывать, что экспериментально измеряют сумму i = i_a+i_k. На участке AB вклад i_k в i значителен, поэтому AB не линеен. На участке ВС наблюдается тафелевская зависимость между Ε и lg i., и наконец, CD — это область предельного диффузионного тока.

Дата добавления: 2014-01-03