Метод двух узлов

Суть метода расчета состоит в том, что по законам Кирхгофа составляется столько уравнений, сколько ветвей с токами.

Метод расчета электрической цепи по законам Кирхгофа

По первому закону Кирхгофа составляется число уравнений на одно меньше, чем узлов в схеме. Например, для рис.9 по первому закону составляется три независимых уравнения:

для узла 1:	I 2 – I 12 + I 31 = 0,	(3.21)
для узла 2:	I 3 + I 12 – I 23 = 0,	(3.22)
для узла 3:	I 1 + I 23 – I 31 = 0.	(3.23)

Уравнения для узла 4 не будет независимым, оно может быть получено из предыдущих трех, (например, путем их сложения и замены знаков).

По второму закону Кирхгофа уравнения составляют для независимых конту­ров (таких контура три) 4 – 1 – 3 – 4; 4 – 2 – 1 – 4; 1 – 2 – 3 (обход по часовой стрелке):

для контура 1:	– R 31 I 31 = E 2 – E 1,	(3.24)
для контура 2:	– R 12 I 12 = E 3 – E 2,	(3.25)
для контура 3:	R 12 I 12 + R 23 I 23 + R 31 I 31 = 0.	(3.26)

Решив систему шести уравнений можно найти шесть токов I ₁, I ₂, I ₃, I ₁₂, I ₂₃, I ₃₁.

Одним из самых распространенных методов расчета электрических цепей яв­ляется метод двух узлов.

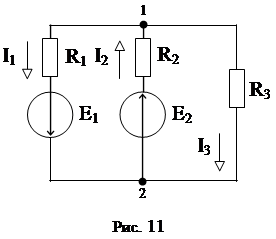
Покажем этот метод на примере рис. 11.

Запишем выражение токов:

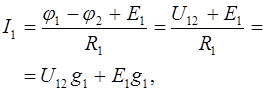
		(3.27)
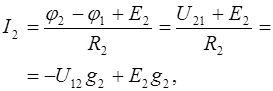
		(3.28)
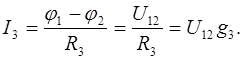
	(3.29)

По первому закону Кирхгофа:

– I 1 + I 2 – I 3 = 0.

(3.30)

Подставим значения токов:

– U 12 g 1 – E 1 g 1 – U 12 g 2 + E 2 g 2 – U 12 g 3 = 0,

(3.31)

откуда находим напряжение U₁₂ между точками 1 и 2:

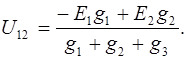
(3.32)

Или в общем виде:

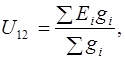
(3.33)

где SE_ig_i – алгебраическая сумма произведений э.д.с. на проводимости (если э.д.с. направлена к первому узлу, то берется со знаком “ + ” и на оборот), В;

Sg_i – сумма проводимостей ветвей, См.

Рассчитав напряжение между двумя узлами, по обобщенному закону Ома на­ходятся токи.

Задание 1 уровня СРС

1. Узел схемы.

2. Ветвь схемы.

3. Контур схемы.

4. Первый закон Кирхгофа.

5. Второй закон Кирхгофа.

6. Эквивалентное сопротивление последовательно соединенных сопротивле­ний.

7. Эквивалентное сопротивление параллельно соединенных сопротивлений.

8. Эквивалентное сопротивление смешанно соединенными сопротивле­ниями.

Задание 2 уровня СРС

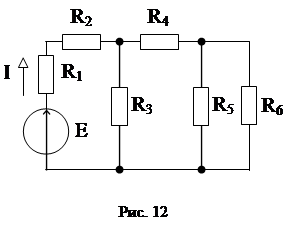Задача 1

Задана расчетная схема цепи (рис. 12).

Е = 200 В; R₁ = 4 Ом; R₂ = 3 Ом; R₃ = 6 Ом; R₄ = 4 Ом; R₅ = 6 Ом; R₆ = 3 Ом.

Найти силу тока I.

Задача 2

На рис. 68 известны R₁₂ = 7 Ом, R₂₃ = 21 Ом, R₃₁ = 21 Ом. Найти на рис. 10 R₁, R₂, R₃.

Задача 3

На рис. 10 известны R₁ = 3 Ом, R₂ = 6 Ом, R₃ = 9 Ом. Найти на рис. 9 R₁₂, R₂₃, R₃₁.

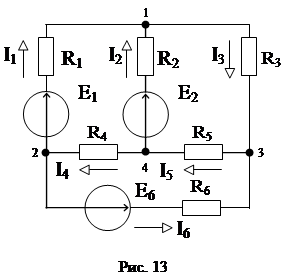
Задача 4

Для расчетной схемы (рис. 13) записать уравнения по первому и второму законам Кирхгофа.

Задача 5

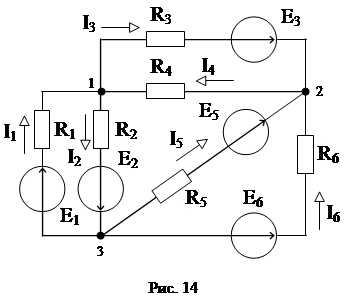
Для заданной расчетной схемы электрической цепи (рис. 14) составьте систему уравнений для расчета токов в ветвях.

Задача 6

Для расчетной схемы рис. 11 известны Е₁ = 100 В, Е₂ = 200 В, R₁ = 10 Ом, R₂ = 5 Ом, R₃ = 5 Ом. Найти токи в ветвях.

Дата добавления: 2014-01-03