Вопрос 3. Дифференциальные уравнения движения Эйлера и Бернулли

Уравнения движения Эйлера устанавливают связь между давлением и скоростью движения жидкости в любой точке потока.

Рассмотрим установившийся поток идеальной жидкости. Вы­делим в потоке элементарный параллелепипед жидкости объемом dV= dxdydz (см. рис.4.7). На элементарный объем жидкости дей­ствуют сила тяжести, инерционная сила и сила гидростатического давления.

Согласно основному принципу динамики сумма проекций всех сил, действующих на движущийся элементарный объем жидкости, равна произведению массы жидкости на ее ускорение.

Если скорость элементарного объема жидкости v, то ускорение равно dv/dτ, а проекции ускорения на оси координат — соответ­ственно

dv_х/ dτ, dv_y/dτ, dv_z/dτ,

где v_x, v_y, v_z — составляющие скорости вдоль осей х, у и z.

Так как мы рассматриваем установившийся поток, то д v_x/ д τ = 0, д v_y/ д τ=0, д v_z/ д τ=0. Производные д v_x/ д τ, д v_y/ д τ, д v_z/ д τ соответ­ствуют изменению во времени значений скоростей v_x, v_y и v_z при перемещении элементарного параллелепипеда жидкости из одной точки пространства в другую.

В соответствии с основным принципом динамики в результате преобразований получено Эйлером

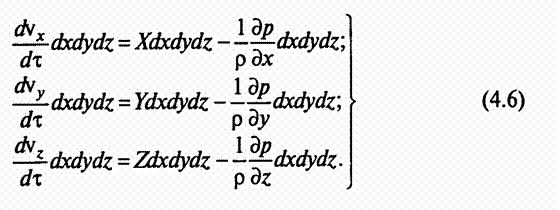
После преобразований из системы уравнений (4.6) получим

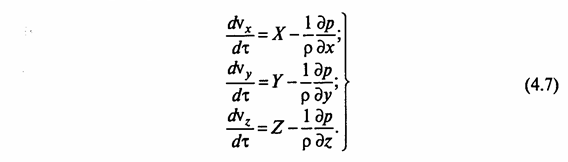
Система уравнений Эйлера (4.7) является системой дифференциальных уравнений движения идеальной жидкости для установившегося потока.

Из дифференциальных уравнений Эйлера получают уравнения Бернулли, широко используемые в гидродинамике.

сти. Единицы измерения динамического напора, как и остальных членов уравнения Бернулли, 1 м или 1 Н • м/Н.

Таким образом, из уравнений (4.8) и (4.9) следует, что при ус­тановившемся движении идеальной жидкости гидродинамический напор остается постоянным для любого сечения потока. Учитывая энергетический смысл каждого члена уравнения Бернулли, можно утверждать, что при установившемся движении идеальной жидкости сумма потенциальной

(z + p/ρg) и кинетической (v²/2g) энергии жидкости — величина постоянная для любого поперечного сече­ния потока.

При изменении поперечного сечения потока потенциальная энергия переходит в кинетическую, и наоборот. Уравнение Бер­нулли выражает частный случай закона сохранения энергии и яв­ляется уравнением энергетического баланса потока идеальной жидкости.

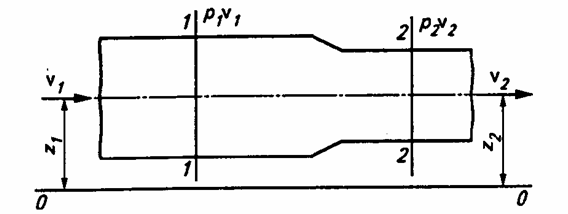
Рис.4.8. Схема трубопровода

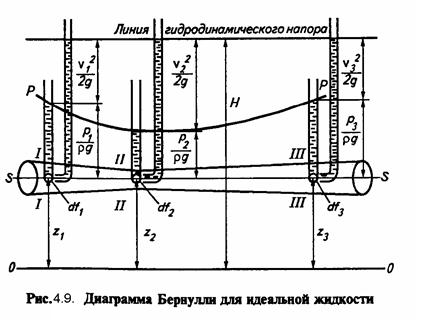
Для реальных (вязких) жидкостей уравнение Бернулли имеет вид:

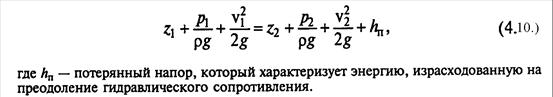
Дата добавления: 2014-01-03