Энтропия. Открытие Клаузиусом энтропии было чисто теоретическим

Открытие Клаузиусом энтропии было чисто теоретическим. Энтропия S вводится через элементарное приращение как

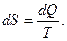(5.13)

При этом теплота 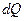не есть приращение какой-то функции, но после деления на температуру Т получается приращение некоторой функции – энтропии. В отличие от теплоты энтропия - функция состояния (как внутренняя энергия, температура или давление). Полученное системой тепло Q зависит от процесса перехода из начального состояния в конечное, приращение же энтропии 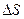совершенно не зависит от процесса, а зависит только от начального и конечного состояний. В интегральной форме выражение (5.13) принимает вид

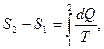
при этом не играет роли, какой именно процесс привел систему из состояния 1 в состояние 2. Процесс перехода может быть даже необратимым. Однако, состояния 1 и 2 должны быть равновесными.

Введенное понятие энтропии позволяет вычислять разность энтропий в двух состояниях, т.е. энтропия вычисляется с точностью до аддитивной постоянной.

Рассмотрим свойства энтропии.

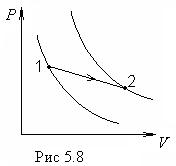
1. Энтропия — функция состояния. Если процесс про­водят вдоль адиабаты, то энтропия системы не меняется. Значит адиабаты — это одновременно и изоэнтропы. Каждой более “высоко” расположенной адиабате (изоэнтропе) отвечает большее значение энтропии. В этом легко убедиться, проведя изотермический процесс между точками 1 и 2, лежащи­ми на разных адиабатах (рис.5.8). В этом процессе Т = const, поэтому 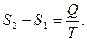Для идеального газа Q равно работе А, совершаемой системой, так как А > 0, то 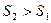. Таким

образом, зная, как выглядит система адиабат, можно легко ответить на во­прос о приращении энтропии при проведении любого процесса между интересующими нас равновесными состояниями 1 и 2.

3. Одно из важнейших свойств энтропии заключается в том, что энтропия замкнутой (т.е. теплоизолированной) макроси­стемы не уменьшается — она либо возрастает, либо остает­ся постоянной.

Принцип возрастания энтропии замкнутых систем пред­ставляет собой еще одну формулировку второго начала термо­динамики.

Величина возрастания энтропии в замкнутой макросистеме может служить мерой необратимости процессов, протекаю­щих в системе. В предельном случае, когда процессы имеют об­ратимый характер, энтропия замкнутой макросистемы не ме­няется.

4. Теорема Нернста. При приближении температуры к абсолютному нулю энтропия макросистемы стремится к нулю

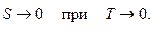
Эта теорема позволяет вычислить абсолютное значение энтропии:

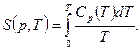
При 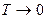теплоемкость 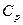всех макросистем должна тоже стремиться к нулю, иначе интеграл не будет сходиться.

Энтропия всегда вычисляется с точностью до аддитивной постоянной. В последнем выражении она принята равной нулю.

Теорема Нернста не может бать выведена из первых двух начал термодинамики, поэтому называется третьим началом термодинамики.

5.8.Примеры вычисления энтропии

1. Основное уравнение термодинамики. Оно представляет собой объединение энтропии с первым началом. Подставив в выражение для первого начала d’Q = TdS , получим для обратимых процессов:

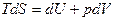. (5.14)

Это уравнение имеет многочисленные применения.

2. Энтропия идеального газа. Пусть начальное и конечное состояния 1 и 2 газа определяются параметрам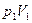и и 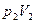. Согласно (5.14) элементарное приращение энтропии газа с учетом того, что dU=C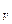dT и pV = νRT, определяется как

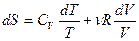. (5.15)

Взяв дифференциал логарифма от vRT = pV получим

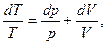(5.16)

и формуле (5.15) можно придать симметричный вид:

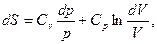
здесь учтено, что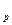 C= C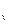+ vR. Проинтегрировав последнее выра­жение, получим

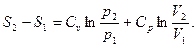
3. Приращение энтропии при необратимом процессе между двумя равновесными состояниями 1 и. 2. Непосредственно счи­тать энтропию по необратимому процессу совершенно невоз­можно. Но энтропия — функция состояния. Этим мы и воспо­льзуемся, проведя между состояниями 1 и 2 какой-нибудь обра­тимый процесс, ничего общего не имеющий с реальным необратимым процессом. Обычно выбирают такой обратимый процесс, по которому расчет проще.

4. Возрастание энтропии при смешении газов. Пусть в двух половинах теплоизолированного сосуда объемом V находятся два идеальных газа , 1и 2, разделенных перегородкой. Температура, давление и количество вещества в обеих половинах одинаково. После удаления перегородки начинается необратимый процесс смешения газов, в результате которого система приходит в равновесное состояние, в котором оба газа равномерно перемешаны. Температура в конечном состоянии окажется прежней, так как газы идеальные и система теплоизолирована. При 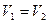приращение энтропии каждого газа равно 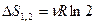, и суммарное приращение энтропии системы

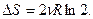
Приращение 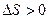, так как процесс необратимый (обратный процесс самопроизвольного разделения газов невероятен).

Последняя формула приводит к парадоксу Гиббса. Допустим, газы 1 и 2 тождественны. Тогда после снятия перегородки энтропия увеличивается, хотя конечное состояние ничем не отличается от начального. Для понимания описанной ситуации существенно заметить, что формула получена только для случая, когда газы различны. Для тождественных газов .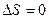

Дата добавления: 2014-01-03; Просмотров: 611; Нарушение авторских прав?; Мы поможем в написании вашей работы!