Задачи, приводящие к понятию производной

Лекция № 5

Тема: «Производная функции»

1.Задачи, приводящие к понятию производной 2. Определение производной. Общее правило дифференцирования 3. Физический и геометрический смысл производной. 4. Необходимое условие дифференцируемости 5. Дифференцирование сложной функции  

Пусть материальная точка движется прямолинейно по закону 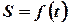, где 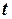- время, 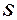- путь, проходимый за время .

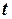Найдем путь, пройденный точкой за некоторый момент времени 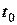, т.е. .

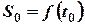Определим скорость 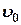материальной точки в момент времени 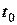(мгновенную скорость).

Для этого рассмотрим другой момент времени 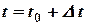. Ему соответствует путь 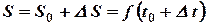, тогда за время 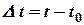точка прошла путь .

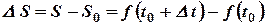Средняя скорость движения 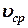за промежуток 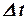определяется отношением 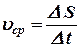пройденного пути ко времени.

Средняя скорость 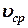является переменной величиной, зависящей от 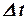, а 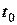- фиксированный момент времени. Она не характеризует движение тела в каждый момент, а показывает, с какой скоростью нужно двигаться равномерно для того, чтобы пройти за время 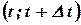расстояние .

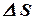При этом движение может происходить различным образом (см. рис.).

От точки 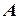к точке 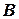можно провести разные линии, но всем этим движениям соответствует одна и та же скорость .

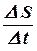Уменьшим 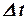, тогда 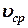будет приближаться к скорости в момент 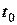, поэтому естественно принять за скорость 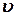в момент времени 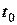предел :

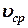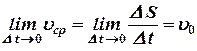
Различные задачи естествознания – такие как определение скорости, ускорения, силы тока, плотности вещества и другие, приводят к одним и тем же вычислениям.

Объемная плотность заряда равна пределу 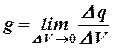отношения заряда к единице объема, когда объем стягивается в точку.

Поверхностная плотность электрического заряда

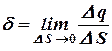
Линейная плотность электрического заряда

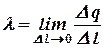
Поэтому в математике изучены подобные пределы и найдены способы их вычисления и названы производной функции.

2. Определение производной. Общее правило дифференцирования

Пусть задана функция 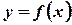, определенная в области 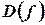и пусть 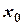- произвольная точка множества 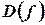. Тогда значение функции в этой точке .

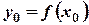Дадим аргументу 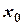приращение 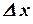, тогд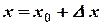а , а

. ,

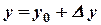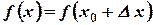тогда .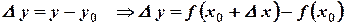

Отношение 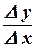характеризуют среднюю скорость изменения функции на промежутке .

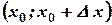Для нахождения скорости изменения функции в точке 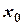надо вычислить предел

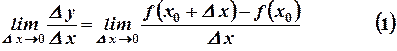
О.2.1. Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, называется производной функции .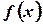

Обозначается производная: 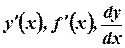. Эти обозначения ввел Лейбниц. Ньютон ввел другие обозначения .

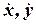0.2.2. Функция называется дифференцируемой в точке 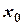, если в этой точке существует конечная производная. Если функция дифференцируема в каждой точке промежутка, то она дифференцируема на промежутке.

Операция вычисления производной называется дифференцированием функции, а раздел математического анализа называется дифференциальным исчислением.

Общее правило дифференцирования.

Для нахождения производной надо:

1) аргументу 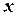дать приращение 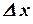и найти значение функции для нового аргумента

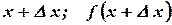
2) найти приращение функции;

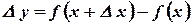
3) найти отношение ;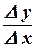

4) найти предел этого отношения, при условии, что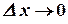

.

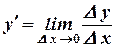Пример: найти производную функции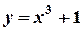

1)

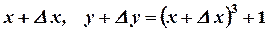
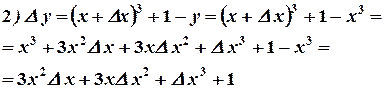
3)

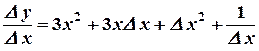
4)

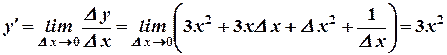
Дата добавления: 2014-01-03