Предельная (финальная) вероятность состояний

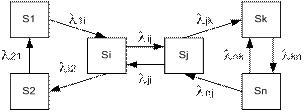
Рассмотрим некоторую систему: S: S₁, S₂, … Sn. Найдём Pi(t)-?, где SPi(t)=1 (1)

t – текущее.

Устремим t ®¥, т.е. рассмотрим ф-е системы на достаточно большом интервале времени. В теории доказывается следующее: Если число состояний системы конечно и возможен переход в каждое из них из любого другого за конечное число шагов, то в системе $ предельные вероятности, кот не зав от начального состояния системы.

Условно считаем, что те ограничения, кот в утверждении, имеют место. Тогда существует предел:

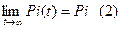- не зав от времени.

Для предельных вер-тей также соблюдается нормировочное условие: SPi(t)=1 (3).

Физ смысл этих предельных вероятностей:

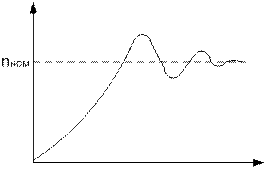
Пример: разгон автомобиля, подъём самолёта.

По истечении длительного времени устанавливается нек стационарный режим, хотя сам процесс не стационарен, где система случайным образом меняет состояние, вер-ть каждого из которых есть величина постоянная. И физ смысл сводится к среднему относительному времени пребывания системы в том или ином состоянии.

] рассматривается работа ВМ, кот имеет 4 сост-я: S1-работает; S2-неисправна; S3-неисправности устраняются; S4-готовится к пуску.

Известны пред вер-ти: P1=0.45, P2=0.15, P3=0.25, P4=0.15.

Они позволяют оценить эф-ть работы системы и не только. Как их получить? По тому же принципу, т.е. с пом ур-й Колмогорова, но в первой части будет 0, т.к. производная от пост вел-ны =0. И получаются обычные алгебраич ур-я.

Дата добавления: 2014-01-03