
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вариньон теоремасы. 1 страница
|
|
|
|
Я могу отказать, если...
Наполнение страниц информацией
Исходники
Количество вариантов дизайна
Предоплата
Сроки выполнения работ
Порядок выполнения работы
ТЗ
группы DESIGN JS
| Заполняет заказчик: | |
| 1. Ссылка на Вашу группу | |
| 2. Вид Вашего оформления (выбрать нужное) 1. Минимальное оформление группы: Нажмите сюда, чтоб увидеть описание данного вида оформления 2. Стандартное оформление группы: Нажмите сюда, чтоб увидеть описание данного вида оформления 3. Полное оформление группы: Нажмите сюда, чтоб увидеть описание данного вида оформления 4. Полное оформление группы с обложкой: Нажмите сюда, чтоб увидеть описание данного вида оформления 5. Полное оформление группы с gif-баннером: Нажмите сюда, чтоб увидеть описание данного вида оформления | |
| 3. Дополнительные услуги Оформление и наполнение внутренних кнопок (картинки, таблицы, текст) | |
| Фон меню · Прикрепите к своему письму VK картинки, которые вы хотите использовать (если такие есть) · Если нет, то опишите подробно тематику картинок и желаемую цветовую гамму (либо поставьте «на усмотрение дизайнера») Если у вас есть логотип, обязательно пришлите его в хорошем разрешении (в формате png) | |
| Название кнопок · Написать название кнопок, в очередности, как будут располагаться во внутреннем меню (пример: о нас/ фото/ видео/ прайс/ акции/ отзывы/ контакты) | |
| Надписи для аватара и баннера · Указать какую информацию пишем на аватаре или баннере (название группы/ф.и.о./телефон/адрес/логотип) | |
| Есть ли на аватаре или баннере призвание к действию · Стрелочка вниз + надпись «вступить в группу/присоединиться/подписаться/жми меню/открыть меню» | |
| Надписи для баннера (если нужно) · Какие надписи будут на баннере (обычно коротко, тезисно 4-5 строк о группе, о преимуществах) Пример: - Прямые поставки из Европы - Гарантия качества - Скидки - Ультрамодные бренды - Бесплатная доставка от 2000 р | |
| Посмотрите в моих работах пример оформления, по которому Вы хотите сделать свою группу · Указать ссылку на пример работы (если такой имеется) |
Это важно!!!
ПРОЧИТАЙТЕ ПРАВИЛА ГРУППЫ:
|
|
|
5. Копирайт © в меню
8. А если результат мне не понравится?
9. Вы можете сделать дизайн дешевле / за какой-нибудь товар?
11. Дизайнер не несёт ответственности за...
Жинақталатын күштер жүйесінің тең әсерлі күшінің кез келген нүктеге қатысты моменті жүйе күштерінің сол нүктеге қатысты моменттерінің геометриялық қосындысына тең: 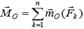
19. Таралған күштер және олардың тең әсерлі күші
Дененің бір нүктесіне түскен күш қадалған күш деп аталады. Бұдан басқа түзу бойымен, жазықтыққа немесе көлемге әсер ететін күштер де бар. Мұндай күштер таралған күштер деп аталады. Жазықтықтағы кез келген күштер жүйесі үшін түзу сызық бойымен таралған күштерді қарастырамыз. Біркелкі таралған күш (жүк) деп әсері түзу сызық бойымен біркелкі таралған күшті айтады. Біркелкі таралған күштің таралу қарқындылығы,яғни жүктелген кесіндінің ұзындық бірлігіне келетін күш беріледі. Бұл жағдайда біркелкі таралған күш тең әсерлі Q күшпен алмастырылады. Оның модулі  ,ал түсу нүктесі жүктелген кесіндінің ортасы болады
,ал түсу нүктесі жүктелген кесіндінің ортасы болады
20. Жазықтықтағы кез келген күштер жүйесінің бас векторы мен бас моменті
Жазықтықтағы кез келген күштер жүйесі үшін де бас вектор барлық күштердің геометриялық қосындысы болады және декарттық координаталар жүйесінің екі өсіне проекцияланады:
|
|
|
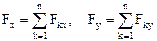 . (1.1)
. (1.1)
Бас вектордың сан шамасы (модулі) мына өрнекпен анықталады:
 , (1.2)
, (1.2)
ал бағыты бағыттаушы косинустардың көмегімен анықталады:
 (1.3)
(1.3)
Бұл жағдайда да О нүктесіне қатысты бас момент барлық күштердің О нүктесіне қатысты моменттерінің алгебралық қосындысы болады:
 (1.4)
(1.4)
Егер денеге күштермен қатар қос күштер әсер етсе, олардың моменттері жүйенің бас моментіне қосылады.
21.Жазықтықтағы кез келген күштер жүйесі тепе теңдігінің аналитикалық шарттары
Күштердің кез келген жазық жүйесі тепе-теңдікте болу үшін оның бас векторы мен кез келген бір О нүктесіне қатысты алынған бас моментінің нөлге тең болуы қажет және жеткілікті, яғни 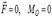 . Бұл шарттар аналитикалық түрде скалярлық тепе-теңдік шарттары түрінде жазылады. Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттарының бірінші түрі: жазықтықтағы кез келген күштер жүйесі тепе- теңдікте болу үшін барлық күштердің екі координата өсіне (х пен у) проекцияларының қосындысы мен күштер жазықтығындағы кез келген О нүктеге қатысты алынған барлық күштердің моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті:
. Бұл шарттар аналитикалық түрде скалярлық тепе-теңдік шарттары түрінде жазылады. Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттарының бірінші түрі: жазықтықтағы кез келген күштер жүйесі тепе- теңдікте болу үшін барлық күштердің екі координата өсіне (х пен у) проекцияларының қосындысы мен күштер жазықтығындағы кез келген О нүктеге қатысты алынған барлық күштердің моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті: 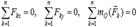 .Жазықтықтағы кез келген күштер жүйесінің аналитикалық тепе-теңдік шарттарын бұдан басқа тағы екі түрде жазуға болады. Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттарының екінші түрі: жазықтықтағы кез келген күштер жүйесі тепе- теңдікте болу үшін барлық күштердің күштер жазықтығындағы бір өске (х) проекцияларының қосындысы мен осы өске перпендикуляр түзуде жатпайтын екі нүктеге (А және В) қатысты алынған барлық күштердің моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті:
.Жазықтықтағы кез келген күштер жүйесінің аналитикалық тепе-теңдік шарттарын бұдан басқа тағы екі түрде жазуға болады. Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттарының екінші түрі: жазықтықтағы кез келген күштер жүйесі тепе- теңдікте болу үшін барлық күштердің күштер жазықтығындағы бір өске (х) проекцияларының қосындысы мен осы өске перпендикуляр түзуде жатпайтын екі нүктеге (А және В) қатысты алынған барлық күштердің моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті: 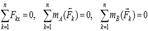 . Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттарының үшінші түрі: жазықтықтағы кез келген күштер жүйесі тепе- теңдікте болу үшін бір түзудің бойында жатпайтын үш нүктеге (А, В және С) қатысты алынған барлық күштердің моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті:
. Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттарының үшінші түрі: жазықтықтағы кез келген күштер жүйесі тепе- теңдікте болу үшін бір түзудің бойында жатпайтын үш нүктеге (А, В және С) қатысты алынған барлық күштердің моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті: 
|
|
|
22. Кеңістіктегі күштер жүйесінің тепе теңдік шарттары
Жинақталатын күштер жүйесі тепе-теңдікте болу үшін оның тең әсерлі күші (немесе барлық күштердің геометриялық қосындысы) нөлге тең болуы қажетті және жеткілікті:  .Кеңістіктегі жинақталатын күштер жүйесінің қажетті және жеткілікті тепе-теңдік шарттары былай жазылады:
.Кеңістіктегі жинақталатын күштер жүйесінің қажетті және жеткілікті тепе-теңдік шарттары былай жазылады: 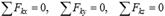 . Қатты денеге әсер ететін кеңістіктегі жинақталатын күштер жүйесі тепе-теңдікте болуы үшін бұл күштердің декарт координата остерінің әрқайсысына проекцияларының қосындысы нөлге тең болуы қажетті және жеткілікті.
. Қатты денеге әсер ететін кеңістіктегі жинақталатын күштер жүйесі тепе-теңдікте болуы үшін бұл күштердің декарт координата остерінің әрқайсысына проекцияларының қосындысы нөлге тең болуы қажетті және жеткілікті.
23. Дененің ауырлық центрін табу әдістері
Дененің ауырлық центрі деп оның барлық нүктелерінің ауырлық күштерін құратын параллель күштер жүйесінің центрін атайды. Ауырлық центрді анықтау әдістерінің 3 түрі бар. 1. Симметрия әдісі. Бұл әдіс біртекті дененің симметрия жазықтығы, симметрия өсі немесе симметрия центрі бар болған кезде қолданылады. Мұндай дененің ауырлық центрі симметрия жазықтығында, не симметрия өсінде, не симметрия центрінде жатады. 2. Бөлшектеу әдісі. Егер берілген дененің пішіні күрделі болса, онда оны ауырлық центрлері оңай табылатын бірнеше бөлшекке бөлеміз. Бөлшектердің ауырлық центрлерін жеке-жеке тауып алғаннан соң біртіндеп дененің ауырлық центрін табамыз. 3. Теріс массалар әдісі. Бұл әдісті қуысты денелерге қолданады. Оны бөлшектеу әдісінің бір түрі деуге болады. Бұл әдісте қуыстарды теріс таңбалы көлемдер, аудандар деп есептейді
|
|
|
.
24. Кейбір біртекті денелердің ауырлық центрлері
Кейбір біртекті денелердің ауырлық центрі. Күрделі денелердің ауырлық центрінің орнын бөлшектеу немесе теріс массалар әдістерімен анықтау үшін күрделі дене бөлінетін қарапайым денелердің ауырлық центрлерін таба білу керек. Осындай біртекті денелерді қарастырайық. Үшбұрыш ауданының ауырлық центрі. Біртекті үшбұрыш ауданының ауырлық центрі (С нүктесі) үшбұрыштың медианаларының қиылысу нүктесінде жатады. Олай болса 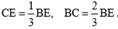 Шеңбер доғасының ауырлық центрі. Центрі О нүктесіндегі радиусы R шеңбердің АВ доғасын қарастырайық. Доғаның орталық бұрышы АОВ = 2α. Егер Ох өсін симметрия өсі етіп алсақ, ауырлық центрі осы өстің бойында жатады. Доғаның біртекті сызық екенін ескерсек, оның ауырлық центрінің
Шеңбер доғасының ауырлық центрі. Центрі О нүктесіндегі радиусы R шеңбердің АВ доғасын қарастырайық. Доғаның орталық бұрышы АОВ = 2α. Егер Ох өсін симметрия өсі етіп алсақ, ауырлық центрі осы өстің бойында жатады. Доғаның біртекті сызық екенін ескерсек, оның ауырлық центрінің  координатасын өрнегінің көмегімен табамыз:
координатасын өрнегінің көмегімен табамыз: 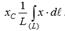 . Дөңгелек сектор ауданының ауырлық центрі. Радиусы R орталық бұрышы 2α дөңгелек сектор ауданының ауырлық центрі Ох симметрия өсінде жатады. ОАВ секторының ауданын О нүктесінен жүргізілген радиустармен n секторға ойша бөлеміз. Шеңбер доғасының ауырлық центрінің өрнегін қолданып радиусы R орталық бұрышы 2α біртекті дөңгелек сектор ауданының ауырлық центрінің координатасының өрнегін алуға болады:
. Дөңгелек сектор ауданының ауырлық центрі. Радиусы R орталық бұрышы 2α дөңгелек сектор ауданының ауырлық центрі Ох симметрия өсінде жатады. ОАВ секторының ауданын О нүктесінен жүргізілген радиустармен n секторға ойша бөлеміз. Шеңбер доғасының ауырлық центрінің өрнегін қолданып радиусы R орталық бұрышы 2α біртекті дөңгелек сектор ауданының ауырлық центрінің координатасының өрнегін алуға болады: 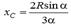
25. Нүкте қозғалысының берілу тәсілдері
Нүкте қозғалысын төмендегі үш әдістердің бірімен береді:
1. Векторлық әдісте нүктенің әр сәтте кеңістіктегі орнын жылжымайтын нүктеден жүргізілген радиус-вектор анықтайды.М әрпімен белгіленген нүкте кеңістікте жылжуына қарай ОМ радиус-векторының шамасы мен бағыты өзгеріп отырады: r=r(t). Бұл радиус вектордың шамасы М нүктесі жылжымайтын О нүктесінен қаншалықты ұзаққа қозғалып кеткенін, ал оның бағыты нүктенің қайсы бағытта жылжығанын белгілейді. Жоғарыдағы өрнек М нүктесінің қозғалу заңы, немесе векторлық қозғалу иеңдеуі деп аталады.
2. Координаттық әдісте нүктенің әр кеңістіктегі орнын оның координаталары анықтайды. М нүктесі OXYZ кеңістігінде қозғалуына қарай оның координаталары да өзгеріп отырады: x=x(t), y=y(t), z=z(t).
Бұл теңдеулер уақыттың өзгеруіне қарай нүктенің кеңістіктегі орнын анықтайды, яғни нүктенің қозғалуын координаттық әдіспен береді. Жоғарыдағы теңдеулерді координаттық әдіспен берілген нүктенің қозғалу заңы деп атайды.Егер нүкте қозғалғанда OXY жазықтығында орналасса, онда теңдеулер мына түрде жазылады:x=x(t),y=y(t).Бұлжағдайда нүктенің қозғалуын полярлық координаттармен анықтауға болады: r=r(t),.
3. Табиғи әдісте нүктенің әр сәтте кеңістіктегі немесе жазықтықтағы орнын доғалық координатамен траекторияның бойынан анықтайды. Бұл әдісті нүктенің траекториясы белгілі болған жағдайда қолданады.. Доғалық координата S уақыттың өзгеруіне қарай өзгереді де, нүктенің траектория бойымен қозғалуын кез-келген мерзімде береді: S=S(t).
26. Қозғалысы векторлық тәсілмен берілген нүктенің жылдамдығы мен үдеуін анықтау
Нүкте жылдамдығының векторы оның радиус-векторынан уақыт бойынша алынған бірінші туындыға тең екен: 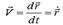 . Берілген уақыттағы нүкте үдеуінің өрнектерін аламыз:
. Берілген уақыттағы нүкте үдеуінің өрнектерін аламыз: 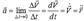 . Демек, нүкте үдеуінің векторы оның жылдамдығының векторынан уақыт бойынша алынған бірінші туындыға немесе радиус-векторынан уақыт бойынша алынған екінші туындыға тең екен. Нүкте үдеуінің векторы әқашан нүкте траекториясының ойыс жағына қарай бағытталады.
. Демек, нүкте үдеуінің векторы оның жылдамдығының векторынан уақыт бойынша алынған бірінші туындыға немесе радиус-векторынан уақыт бойынша алынған екінші туындыға тең екен. Нүкте үдеуінің векторы әқашан нүкте траекториясының ойыс жағына қарай бағытталады.
27. Қозғалысы табиғи тәсілмен берілген нүктенің жылдамдығы мен үдеуін анықтау
Табиғи әдіс. Бұл әдіспен берілген нүкте үшін жылдамдықтың жалпы анықтамасына сәйкес түрлендірулер жасағаннан кейін, қозғалысы табиғи әдіспен берілген нүкте жылдамдығы векторының өрнегін аламыз: 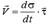 Нүкте жылдамдығы векторының жанама өске проекциясын анықтайтын
Нүкте жылдамдығы векторының жанама өске проекциясын анықтайтын 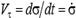 белгілеу ендірсек, онда жылдамдық векторы былай өрнектеледі:
белгілеу ендірсек, онда жылдамдық векторы былай өрнектеледі: 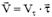 . Егер
. Егер 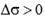 болса, жылдамдық векторы нүкте траекториясына жанама бойынша қозғалыстың оң бағытына қарай ал
болса, жылдамдық векторы нүкте траекториясына жанама бойынша қозғалыстың оң бағытына қарай ал 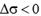 болса – теріс бағытына қарай бағытталады. Жылдамдықтың сан шамасы:
болса – теріс бағытына қарай бағытталады. Жылдамдықтың сан шамасы:  Нүкте үдеуін анықтау үшін қозғалыс барысында
Нүкте үдеуін анықтау үшін қозғалыс барысында  векторының бағытының өзгеретінін ескере отырып, оның жылдамдығы векторынан бірінші туынды аламыз:
векторының бағытының өзгеретінін ескере отырып, оның жылдамдығы векторынан бірінші туынды аламыз: 
28. Қозғалысы координаталық тәсілмен берілген нүктенің жылдамдығы мен үдеуін анықтау
Нүкте қозғалысы координаталық әдіспен берілсе оның радиус-векторын декарттық координата жүйесінің тұрақты 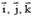 вектолары арқылы жазуға болады
вектолары арқылы жазуға болады 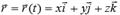 өрнекті ескере отырып нүктенің жылдамдық векторының декарттық координата өстеріне проекцияларын аламыз:
өрнекті ескере отырып нүктенің жылдамдық векторының декарттық координата өстеріне проекцияларын аламыз:  . Нүкте жылдамдығының сан шамасы:
. Нүкте жылдамдығының сан шамасы: 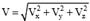 . Нүкте үдеуінің сан шамасын:
. Нүкте үдеуінің сан шамасын: 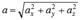
29. Нүктенің жанама және нормаль удеулері
Үдеудің жанама өске проекциясы нүктенің жанама (тангенциальдық)үдеуі деп: 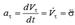 .Ал бас нормальға проекциясы нүктенің нормаль үдеуі деп аталады:
.Ал бас нормальға проекциясы нүктенің нормаль үдеуі деп аталады: 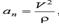
30. Қатты дененің ілгерлемелі қозғалысы. Ілгерлемелі қозғалыстағы дене нүктелерінің траекториясы, жылдамдығы, үдеуі туралы теорема.
Дене қозғалғанда денеде белгіленген бір түзу кесінді өзіне өзі параллель болып отырса, дененің қозғалысын ілгерілемелі қозғалыс деп атаймыз. Бұл жағдайда дене нүктелерінің қозғалысы келесі теоремамен анықталады: ілгерілемелі қозғалыстағы дененің барлық нүктелері бірдей траекториялар сызады, берілген уақытта барлық нүктелерінің жылдамдықтары м Қатты дененің айналмалы қозғалысының негізгі кинематикалық сипаттамаларына бұрыштық жылдамдық пен бұрыштық үдеу жатады. Бұл ұғымдарды енгізу үшін дене 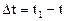 уақытта Dj бұрышқа бұрылды деп санаймыз. Сонда Dj - дің Dt - ға қатынасы Dt уақыттағы дененің орташа бұрыштық жылдамдығы деп аталады:
уақытта Dj бұрышқа бұрылды деп санаймыз. Сонда Dj - дің Dt - ға қатынасы Dt уақыттағы дененің орташа бұрыштық жылдамдығы деп аталады:
 . ен үдеулері бірдей болады..Дененің бұрыштық жылдамдығының алгебралық шамасы айналу бұрышынан уақыт бойынша алынған бірінші туындыға тең екен. Осы шаманың модулін дененің бұрыштық жылдамдығы деп атаймыз дененің бұрыштық үдеуінің алгебралық шамасы бұрыштық жылдамдықтың алгебралық шамасынан уақыт бойынша алынған бірінші туындыға немесе айналу бұрышынан алынған екінші туындыға тең екен. Осы шаманың модулін дененің бұрыштық үдеуі дейтін боламыз. Егер кез келген дене ілгерілемелі қозғалыста болса, онда оның барлық нүктелері бірдей жылдамдықпен, бірдей үдеумен және бірдей траекториямен қозғалады.
. ен үдеулері бірдей болады..Дененің бұрыштық жылдамдығының алгебралық шамасы айналу бұрышынан уақыт бойынша алынған бірінші туындыға тең екен. Осы шаманың модулін дененің бұрыштық жылдамдығы деп атаймыз дененің бұрыштық үдеуінің алгебралық шамасы бұрыштық жылдамдықтың алгебралық шамасынан уақыт бойынша алынған бірінші туындыға немесе айналу бұрышынан алынған екінші туындыға тең екен. Осы шаманың модулін дененің бұрыштық үдеуі дейтін боламыз. Егер кез келген дене ілгерілемелі қозғалыста болса, онда оның барлық нүктелері бірдей жылдамдықпен, бірдей үдеумен және бірдей траекториямен қозғалады.
31. Қатты дененің айналмалы қозғалысының анықтамасы. Дененің айналу осьі.
Егер дене қозғалғанда оның кез келген екі нүктесі қозғалмайтын (орын ауыстырмайтын) болса, ондай қозғалысты тұрақты өсті айнала қозғалу дейміз. Қозғалмайтын екі А, В нүктелерден өтетін түзуді айналмалы қозғалыстың өсі дейміз. Аталған А, В нүктелердің аралығы өзгермейтін болғандықтан, АВ өсінде жатқан барлық нүктелер қозғалысқа қатыспайды. Өс бойында жатпайтын нүктелер шеңбер бойымен қозғалады. Шеңберлер өске перпендикуляр жазықтықтарда жатады. Олардың центрлері өстің бойында болады. Қозғалмайтын екі нүктені қосатын түзу айналу өсі деп аталады. Айналу өсінде жататын нүктелердің барлығы қозғалмайды.
Ал айналу өсінде жатпайтын нүктелер центрлері айналу өсінде жататын, жазықтықтары айналу өсіне перпендикуляр шеңберлер сызады.
32. Қатты дененің айналмалы қозғалысы Айналмалы қозғалыстағы дененің кез келген нүтесінің жылдамдығы
Дененің тұрақты өсті айнала қозғалуы. Егер дене қозғалғанда оның кез келген екі нүктесі қозғалмайтын (орын ауыстырмайтын) болса, ондай қозғалысты тұрақты өсті айнала қозғалу дейміз. Қозғалмайтын екі А, В нүктелерден өтетін түзуді айналмалы қозғалыстың өсі дейміз. Аталған А, В нүктелердің аралығы өзгермейтін болғандықтан, АВ өсінде жатқан барлық нүктелер қозғалысқа қатыспайды. Өс бойында жатпайтын нүктелер шеңбер бойымен қозғалады. Шеңберлер өске перпендикуляр жазықтықтарда жатады. Олардың центрлері өстің бойында болады.
Кез келген нүкте жылдамдығы 
33. Қатты дененің айналмалы қозғалысы Айналмалы қозғалыстағы дененің бұрыштық жылдамдығы мен бұрыштық үдеуі
Егер дене қозғалғанда оның кез келген екі нүктесі қозғалмайтын (орын ауыстырмайтын) болса, ондай қозғалысты тұрақты өсті айнала қозғалу дейміз. Қозғалмайтын екі А, В нүктелерден өтетін түзуді айналмалы қозғалыстың өсі дейміз. Аталған А, В нүктелердің аралығы өзгермейтін болғандықтан, АВ өсінде жатқан барлық нүктелер қозғалысқа қатыспайды. Өс бойында жатпайтын нүктелер шеңбер бойымен қозғалады. Шеңберлер өске перпендикуляр жазықтықтарда жатады. Олардың центрлері өстің бойында болады.
Айналу бұрышының 1-ші туындысы дененің бұрыштық жылдамдығын  және 2-ші туындысы бұрыштық үдеуін
және 2-ші туындысы бұрыштық үдеуін 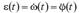 береді.
береді.
34. Қатты дененің айналмалы қозғалысы Айналмалы қозғалыстағы дененің кез келген нүктесінің үдеуі
Егер дене қозғалғанда оның кез келген екі нүктесі қозғалмайтын (орын ауыстырмайтын) болса, ондай қозғалысты тұрақты өсті айнала қозғалу дейміз. Қозғалмайтын екі А, В нүктелерден өтетін түзуді айналмалы қозғалыстың өсі дейміз. Аталған А, В нүктелердің аралығы өзгермейтін болғандықтан, АВ өсінде жатқан барлық нүктелер қозғалысқа қатыспайды. Өс бойында жатпайтын нүктелер шеңбер бойымен қозғалады. Шеңберлер өске перпендикуляр жазықтықтарда жатады. Олардың центрлері өстің бойында болады.
Толық үдеу модулі 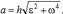 .Жанама үдеу траектория жанамасының бойымен бағытталады
.Жанама үдеу траектория жанамасының бойымен бағытталады 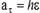 , нормальдық үдеу радиус бойымен центрге бағытталады
, нормальдық үдеу радиус бойымен центрге бағытталады 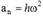
35. Жазық-параллель қозғалыстағы дененің кез келген нүктесінің жылдамдығы
Егер дененің барлық нүктелері қозғалмайтын жазықтыққа параллель көшіп отырса, онда дененің қозғалысын жазық-параллель қозғалыс деп атаймыз. Дененің кез келген М нүктесінің жылдамдығы полюс ретінде алынған дененің басқа А нүктесінің жылдамдығы мен М нүктесінің полюсті денемен бірге айналғанда алатын жылдамдығының геометриялық қосындысына тең. 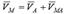 мұндағы
мұндағы 
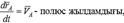
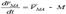 нүктенің дене үйек
нүктенің дене үйек
нүктесін айналғанда алатын жылдамдығы.
36. Жазық-параллель қозғалыстағы дененің кез келген нүктесінің үдеуі
Егер дененің барлық нүктелері қозғалмайтын жазықтыққа параллель көшіп отырса, онда дененің қозғалысын жазық-параллель қозғалыс деп атаймыз. Жазық-параллель қозғалыстағы дене нүктесінің үдеуін табу үшін 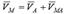 өрнектен уақыт бойынша туынды аламыз. Сонда
өрнектен уақыт бойынша туынды аламыз. Сонда 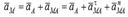 , мұндағы
, мұндағы 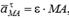
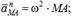
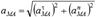 .Айналмалы қозғалыстағы дененің М нүктесінің
.Айналмалы қозғалыстағы дененің М нүктесінің  үдеуінің модулі мен бағыты былай табылады.
үдеуінің модулі мен бағыты былай табылады. 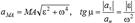 Есеп шығару барысында:
Есеп шығару барысында: 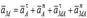 түрінде жазған ыңғайлы.
түрінде жазған ыңғайлы.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 2132; Нарушение авторских прав?; Мы поможем в написании вашей работы!