Граф состояний системы (State Graph)

Пусть система состоит из N элементов и каждый из них может пребывать в дискретных состояниях . Тогда количество состояний M, в которых может находится система определяется соотношением 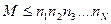. Наличие знака меньше обусловлено тем, что возможны случаи, что определенные состояния различных элементов несовместны по физическим, организационным или другим причинам.

В результате отказов и восстановлений система в дискретные моменты времени будет переходить из одного состояния в другое. При этом в процессе длительной эксплуатации она может побывать в каждом из состояний многократно. Такое функционирование системы можно представить в виде графа, где вершинами графа будут являться различные состояния, а дугами графа – возможные переходы между состояниями.

Состояния обычно нумеруются. Все состояния (множество ) можно разделить на две группы: работоспособные (подмножество 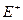) и неработоспособные (подмножество ). Первые можно обозначать кружками, а вторые квадратами. В графе состояний можно выделить одно начальное состояние. Также, если система неремонтируемая, или существуют такие состояния, откуда восстановление системы невозможно, то граф будет содержать поглощающие вершины, для которых нет исходящих дуг.

Обычно с дугой ассоциируется численная величина – интенсивность перехода, которая численно может быть равна интенсивности отказа/восстановления элемента, в результате отказа/восстановления которого происходит смена состояния системы.

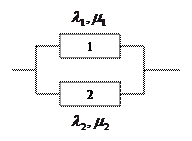
Рассмотрим граф состояний для системы заданной следующей структурной схемой:

Все элементы системы восстанавливаемые. Система неработоспособна, если неработоспособен любой из её элементов. Во время восстановления i-ого элемента, остальные выключены и не отказывают. Каждый элемент характеризуется интенсивностями отказов и восстановлений и .

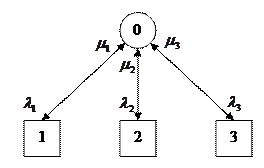
Состояние 0 – все элементы работоспособны. Состояния 1-3, соответственно, состояния восстановления 1,2 или 3 элемента после отказа. Очевидно, что из 0-ого состояния в i-ое отказовое система может попасть с интенсивностью , а вернуться обратно с интенсивностью .

Вид графа восстанавливаемой системы непосредственно зависит от числа обслуживающих бригад и дисциплины обслуживания. Чтобы показать рассмотрим пример функционирования дублированной системы, состоящей из двух параллельно работающих элементов, при различных вариантах восстановления:

a) систему обслуживают две бригады, и элементы могут восстанавливаться параллельно;

b) систему обслуживает одна бригада с прямым приоритетом, т.е. восстанавливаться в первую очередь будет тот, элемент который отказал раньше;

c) систему обслуживает одна бригада с обратным приоритетом, т.е. восстанавливаться будет последний отказавший элемент, прерывая восстановление предыдущего элемента;

d) систему обслуживает одна бригада с заданным приоритетом: всегда сначала восстанавливать первый элемент.

Для случая (a) граф состояний будет иметь следующий вид:

Состояния: 0 – оба элемента исправны; 1 – восстанавливается первый элемент, второй работает; 2 – восстанавливается второй элемент, первый работаю; 3 – восстанавливаются оба элемента.   В состояния 1 и 2 система может перейти из состояния 0 в результате отказа соответствующего элемента. Если отказавший элемент будет восстановлен, то система вернется в состояние 0. Если же во время восстановления одного элемента, откажет и дублирующий – система перейдет в неработоспособное состояние 3. Как только будет восстановлен любой из элементов (которые в состоянии 3 восстанавливаются одновременно и параллельно), система вернется в состояние 1 или 2.

Рассмотрим случай (b):

Состояния: 0, 1, 2 – те же, что и в случае (a); 3 – восстанавливается элемент 1, элемент 2 ожидает восстановления; 4 – восстанавливается элемент 2, элемент 1 ожидает восстановления.   В состояние 3 система попадет из состояния 1, если первый элемент не успеет восстановиться раньше, чем откажет второй. Но прямой приоритет, обязывает дождаться восстановления элемента 1, и только потом уже приступать к восстановлению элемента 2. Поэтому из состояния 3 можно попасть только в состояние 2.   Аналогичные (симметричные) рассуждения применимы для состояний 2 и 4

Рассмотрим случай (c):

Состояния – те же, что и в случае (b):   В этом случае из состояния 1 в результате отказа второго элемента система попадет в состояние 4 – в силу обратного приоритета: восстановление первого элемента будет приостановлено до восстановления элемента 2. Тогда система вернется в состояние 1.   Аналогичные (симметричные) рассуждения применимы для состояний 2 и 3

Рассмотрим случай (d):

Состояния: 0, 1, 2 – те же, что и в случае (a); 3 – восстанавливается элемент 1, элемент 2 ожидает восстановления (как в случаях (b) и (c)).   Здесь состояние 4 из случаев (b) и (c) отсутствует по организационным причинам – элемент 1 никогда не ожидает восстановления. Поэтому при двух отказах, система будет попадать в состояние 3, откуда будет возвращаться только в состояние 2, по окончанию ремонта элемента 1.

Из приведенных примеров видно, что граф состояний восстанавливаемой системы полностью определяется её структурой (схемой расчета надежности), надежностью устройств, их ремонтопригодностью, числом ремонтных бригад, дисциплиной обслуживания и видом восстановления. В нем содержится вся необходимая для расчетов информация. К тому же такое представление наглядно.

Но если система состоит из большого количества элементов, граф становится очень громоздким. Для составления таких графом нужна формализованная процедура, работающая на основе более простых моделей.

Дата добавления: 2014-01-03