Лекция. Измерение связей неколичественных переменных

Методы корреляционного и регрессионного анализа предназна­чены для количественных переменных, т. е. переменных, измерен­ных на интервальной шкале. В практических задачах асе чаще тре­буется измерение связей неколичественных переменных, измерен­ных на номинальных и порядковых шкалах. Это вызвано повышением внимания к изучению социальных процессов, где ве­лика доля нечисловой информации. Кроме того, актуализировалось понятие «коммерческая тайна». Так, при опросах менеджеров фирм об объеме расчетов с поставщиками, соотношении дебитор­ской и кредиторской задолженности респонденты предпочитают не давать точные количественные ответы, а указывать на измене­ние ситуации: улучшилось, ухудшилось, осталось без изменения; Повысилась, понизилась, сохранилась на прежнем уровне и т. д. Развитие конкурентных рынков способствовало разработке методик Построения рейтингов фирм, банков, учебных заведений и т. д. Рейтинг — по сути порядковая переменная, и для изучения зависи­мости рейтинга от каких-либо характеристик должны использовать­ся меры связи, предназначенные для порядковых переменных. При ^этом единицам совокупности присваиваются ранги по разным признакам, т.е. порядковые номера единиц совокупности в ранжированном ряду. Связь между ними определяется коэффициентом кор­реляции рангов. Наиболее распространенными мерами связей между грядковыми переменными являются коэффициенты корреляции рангов Спирмена и Кендэлла (названные по фамилиям английских ученых, разработавших эти меры связи).

Формула коэффициента корреляции рангов Спирмена основана на формуле коэффициента парной корреляции:

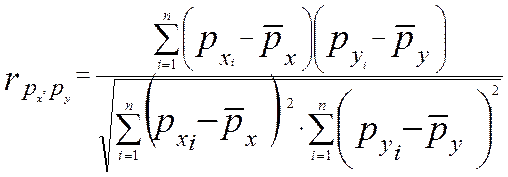
где 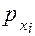— ранг i‑й единицы совокупности по переменной х; - средний ранг по переменной х; —ранг i-й единицы совокупности по переменной у; 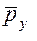-средний ранг по переменной у.

Очевидно, что коэффициент ранговой корреляции изменяется так же как и коэффициент парной корреляции, в интервале от -1 до 1 (по абсолютной величине —[0,1]).

Путем преобразований приведенной формулы Ч. Спирмен полу­чил выражение коэффициента ранговой корреляции, которое обычно используется:

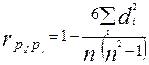
где 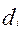- разность рангов по переменным х и у для i-й единицы совокупности; n— число наблюдений.

Иногда коэффициент ранговой корреляции обозначается грече­ской буквой ρ.

Пример. Пять фирм, производящих молочные продукты, проранжированы по рангам, соответствующим оценке покупателями качества их продукции. Параллельно получены ранги этих фирм по результатам опросов магазинов розничной торговли. Получены следующие результаты (таблица 1).

Таблица 1 ‑ Расчет коэффициента ранговой корреляции

Фирма	Ранг покупателей	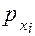Ранг продавцов
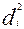
А
Б
В
Г
Д

.

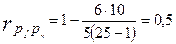В данном случае связь умеренная: оценки покупателей не слишком коррелируют с оценками продавцов.

Измерим ту же корреляцию с помощью коэффициента Кендэлла τ:

,

где s — фактическая сумма рангов; 1/2n·(n-1)—максимальная сумма рангов.

По данным примера:

s = (3 - 1) + (3 - 0) + (0 - 2) + (0 - 1) = 2

s рассчитывается по рангам у. Для каждого ранга определяется число рангов выше данного и вычитается число рангов ниже данного. И так для всех единиц. В результате

,

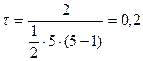т. е. коэффициент τ дал еще более строгую оценку измеряемой свя­зи. При большом числе наблюдений и нетесных связях пример­но в 2,5 раза больше τ.

Рассмотрим, как изучается связь между номинальными переменны­ми. Здесь значения переменных не участвуют в измерении связи. Вся информация о наличии или отсутствии связи содержится лишь в час­тотах появления сочетаний признаков х и у. Основой изучения связи номинальных переменных служит таблица сопряженности — двумерное распределение единиц совокупности по переменным х и у (таблица 2).

Таблица 2 - Таблица сопряженности

Переменная х	Переменная y	Итого
х	y1	y2	y3	...	yp
х1	n11	n12	n13	...	n1p	n1
х2	n21	n22	n23	...	n2p	n2
х3	n31	n32	n33	...	n3p	n3
...	...	...	...	...	...	...
хm	nm1	nm2	nm3	...	nmp	nm
Итого	n.1	n.2	n.3	...	n.p	n

В итоговых частотах точкой обозначено суммирование по одному из подстрочных значков.

Частоты, стоящие в клетках таблицы, называются клеточными час­тотами. Именно по их значениям судят о наличии и тесноте связи. Если единицы совокупности концентрируются в диагональных клетках таблицы, то налицо наличие связи; если же такой концентрации не наблюдается — связи может не быть.

Факт наличия связи устанавливается с помощью критерия χ²:

,

где -фактическая клеточная частота, т. е. число единиц с i-м зна­чением признака х и
j-м значением признака y, 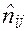- теоретическая: клеточная частота, отвечающая предположению о независимости переменных х и у, т. е. отсутствию связи.

Как известно, вероятность двух независимых событий равна про­изведению их вероятностей:

.

Для того чтобы от вероятностей (частостей) перейти к частотам, вероятность нужно умножить на п. Получаем формулу теоретической клеточной частоты:

,

т. е. итог по строке нужно умножить на итог по столбцу и разделить на общее число данных.

Сумма теоретических частот во всех клетках таблицы равна обще­му числу наблюдений п. Сумма теоретических частот по строкам и столбцам таблицы равна соответственно 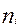и 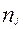. Таким образом, тео­ретические частоты — это перераспределение исходных данных в предположении, что связь между переменными х и у отсутствует.

Величина χ² показывает, насколько велико расхождение фактиче­ских частот с теми, которые были бы, если бы х и у были независимыми. Такое расхождение так или иначе всегда будет, поэтому существует таблица критических значений критерия χ², которая содержит предельно возможное значение χ² отвергает предположение о независимости переменных.

Распределение χ² зависит от числа степеней свободы и уровне значимости α. Число степеней свободы определяется следующим об­разом:

d.f. = mp– m– p+ 1 = (m– 1)(p– 1),

где т - число категорий переменной х, или число строк таблицы со­пряженности; р - число категорий переменной у, или число столбцов таблицы сопряженности; тр - число клеток таблицы сопряженности.

Уровень значимости - это вероятность отклонить гипотезу о неза­висимости переменных при условии, что она верна. Обычно уровень значимости принимается равным α = 0,05 или 0,01 (5% или 1%).

Вычисленное по вышеуказанной формуле значение χ²(χ²_табл.) сравнивается с критическим (табличным) значением χ² при данном числе сте­пеней свободы и принятом уровне значимости (χ²_α.d.f.). Если χ²_факт. > χ²_α.d.f., то делается вывод о наличии связи признаков х и у, и, наоборот, если χ²_факт. ≤ χ²_α.d.f., то гипотеза о независимости х и у не отклоняется, т.е. наличие связи не может считаться доказанным.

Пример. При анализе работы фирмы, оказывающей сантехниче­ские услуги как компаниям, так и индивидуальным заказчикам, воз­никла необходимость оценить, нет ли связи между типом клиента и качеством обслуживания. С этой целью была построена следующая таблица сопряженности (таблица 3).

Таблица 3 - Соотношение типа клиента и качества обслуживания

Клиенты	Качество обслуживания	Количество обслуженных
Устраивает	Не устраивает
Компании		133,2		34,8
Индивидуальные заказчики		368,8		96,2
Итого

Анализируя данные табл. 7.12, видим, что среди обслуженных компаний лишь 10,7 % высказали претензии к качеству обслуживания, тогда как из индивидуальных заказчиков доля тех, кого не устроило качество работ, составила 24,3 %. Чтобы удостовериться, что связь ме­жду типом клиента и качеством обслуживания существует, вычислим значения. Для этого рассчитаем теоретические частоты, которые за­пишем в клетках таблицы в правом верхнем углу.

; ;

; .

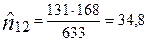Учитывая, что мы имеем дело с таблицей 2x2 (четырехклеточной) можно было бы не вычислять и , а получить их как разность и .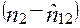

Поскольку теоретические клеточные частоты — рассчитанные вели­чины, они могут быть нецелыми числами. Сумма всех теоретических Частот равна n = 633, итоги по строкам и столбцам таблицы равны итоговым частотам.

Табличное значение χ² при числе степеней свободы d.f.= (2 - 1)(2 - 1) = 1 и уровне значимости α = 0,05 (т. е, при 95% доверительной вероятности) составляет 3,84.

χ²_факт.> χ²_табл., следовательно, наличие связи может считаться доказанным: действительно, тип клиента сказывается на качестве обслуживания.

После того как связь установлена, приступают к ее измерению, χ² не является мерой связи. Его величина зависит от объема совокупности, числа строк и столбцов таблицы. 0≤ χ²≤∞, т. е. значение может быть сколь угодно большим.

Измерение тесноты связи производят с помощью коэффициентов взаимной сопряженности. Все они основаны на нормировании χ²: погашении зависимости от числа наблюдений и размерности таблицы.) Все эти меры связи изменяются в интервале [0.1].

Коэффициент взаимной сопряженности К. Пирсона:

,

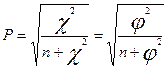где .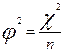

Этот коэффициент не принимает во внимание число категорий для переменных х и у. Более совершенным является коэффициент сопряженности А. А. Чупрова:

.

Этот коэффициент в случае, если таблица не квадратная, никогда не достигает 1.

Модификацией этого коэффициента является коэффициент взаим­ной сопряженности Г. Крамера:

,

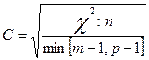т. е. в знаменателе подкоренного выражения берется минимальная из величин: число строк без единицы либо число столбцов без единицы. Для квадратных таблиц C=T. По данным примера:

.

Тогда P = 0,147; T = C = 0,147.

Если таблица сопряженности не является четырехклеточной, то P>(T, C).

Коэффициент контингенции определяется следующим образом:

По данным примера:

Для таблиц 2x2 разработаны специальные меры связи. Основные из них — коэффициент ассоциации и коэффициент контингенции. Коэффициент ассоциации равен:

Коэффициент контингенции дал значительно более высокую оценку тесноты связи.

.

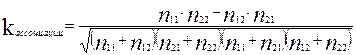По данным примера:

.

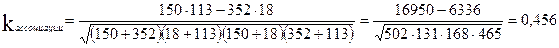Недостаток этого коэффициента в том, что если хотя бы одна из клеточных частот равна нулю, то коэффициент контингенции становится равным единице.

Таким образом, для каждого уровня измерения переменных разра­ботаны соответствующие меры связи.

Значение t-критерия Стьюдента при уровне значимости 0,10, 0,05, 0,01

Число степеней свободы d.f.	Р	d.f.	Р
0,10	0,05	0,01	0,10	0,05	0,01
	6,3138	12,706	63,657		1,7341	2,1009	2,8784
	2,9200	4,3027	9,9248		1,7291	2,0930	2,8609
	2,3534	3,1825	5,8409		1,7247	2,0860	2,8453
	2,1318	2,7764	4,6041		1,7207	2,0796	2,8314
	2,0150	2,5706	4,0321		1,7171	2,0739	2,8188
	1,9432	2,4469	3,7074		1,7139	2,0687	2,8073
	1,8946	2,3646	3,4995		1,7109	2,0639	2,7969
	1,8595	2,3060	3,3554		1,7081	2,0595	2,7874
	1,8331	2,2622	3,2498		1,7056	2,0555	2,7787
	1,8125	2,2281	3,1693		1,7033	2,0518	2,770?
И	1,7955	2,2010	3,1058		1,7011	2,0484	2,7633
	1,7823	2,1788	3,0545		1,6991	2,0452	2,7564
	1,7709	2,1604	3,012Э		1,6973	2,0423	2,7500
	1,7613	2,1448	2,9768		1,6839	2,0211	2,7045
	1,7530	2,1315	2,9467		1,6707	2,0003	2,6603
	1,7459	2,1199	2,9208		1,6577	1,9799	2,6174
	1,7396	2,1098	2,8982	∞	1,6449	1,9600	2,5758

Значение χ² - критерия Пирсона при уровне значимости 0,10, 0,05, 0,01

d.f.	0,10	0,05	0,01	d,f,	0,10	0,05	0,01
	2,71	3,84	6,63		29,62	32,67	38,93
	4,61	5,99	9,21		30,81	33,92	40,29
	6,25	7,81	11,34		32,01	35,17	41,64
	7,78	9,49	13,28		33,20	16,42	42,98
	9,24	11,07	15,09		34,38	37,65	44,31
	10,64	12,59	16,81		35,56	38,89	45,64
	12,02	14,07	18,48		36,74	40,11	46,96
	13,36	15,51	20,09		37,92	41,34	48,28
	14,68	16,92	21,67		39,09	42,56	49,59
	50,99	18,31	23,21		40,26	43,77	50,89
	17,28	19,68	24,72		51,80	55,76	63,69
	18,55	21,03	26,22		63,17	67,50	76,15
	19,81	22,36	27,69		74,40	79,08	88,38
	21,06	23,68	29,14		85,53	90,53	100,4:
	22,31	25,00	30,58		96,58	101,88	112,33
	23,54	26,30	32,00		107,56	113,14	124,12
	24,77	27,59	33,41		118,50	124,34	135,81
	25,99	28,87	34,81
	27,20	30,14	36,19
	28,41	31,14	37,57

Критические значения коэффициентов корреляции для уровней значимости 0,05, 0,01

	α = 0,05	α = 0,01	d.f.	α = 0,05	α = 0,01
	0,996917	0,9998766		0,4555	0,5751
	0,995000	0,990000		0,4438	0,5614
	0,8783	0,95873		0,4329	0,5487
	0,8114	0,91720		0,4227	0,5368
	0,7545	0,8745		0,3809	0,4869
	0,07067	0,8343		0,3494	0,4487
	0,6664	0,7977		0,3246	0,4182
	0,6319	0,7646		0,3044	0,3932
	0,6021	0,7348		0,2875	0,3721
	0,5760	0,7079		0,2732	0,3541
	0,5529	0,6835		0,2500	0,3248
	0,5324	0,6614		0,2919	0,3017
	0,5139	0,6411		0,2172	0,2830
	0,4973	0,6226		0,2050	0,2673
	0,4821	0,6055		0,1946	0,2540
	0,4683	0,5897

Для простой корреляции d.f. на 2 меньше, чем число пар вариан­тов; в случае частной корреляции необходимо также вычесть число исключаемых переменных.

Дата добавления: 2014-01-04