Вопрос 3.Процентные ставки и методы их начисления

Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется процессом дисконтиро­вания, искомая величина – приведенной суммой, а используемая в операции ставка – ставкой дисконтирования. В данном случае речь идет о движении от будущего к настоящему.

В финансовых вычислениях первый показатель имеет еще названия «процентная ставка», «процент», «рост», «ставка процента», «норма прибыли», «доходность», а второй – «учетная ставка», «дисконт», «ставка дисконтирования».

Оба показателя выражаются либо в долях, либо в процентах.

Итак, в любой финансовой операции всегда присутствуют три величины, две из которых заданы, а одна является искомой.

Процесс, в котором заданы исходная сумма и процент­ная ставка, в финансовых вычислениях называется процессом наращения, искомая величина – наращенной суммой, а используемая в операции ставка – ставкой наращения. В данном случае речь идет о движении денежного потока от настоящего к будущему.

Экономический смысл финансовой операции, задаваемой формулой (1) – процесса наращения, состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Из формулы (1) получаем:

FV = PV + PV • и PV • 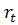> 0 видно, что время генерирует деньги.

Определить на основании величины FV, т.е. будущей стоимости «сегодняшней» величины PV при заданном уровне доходности можно по формуле (2):

PV = FV· (1- 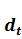) и 1- < 1, опять приходим к выводу, что время генерирует деньги.

Необходимость учета временной ценности денег проявляется, прежде всего, в ссудо-заемных операциях. Предоставляя денежные средства в долг, их владелец получает определенный доход в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка времени. Поскольку стандартным временным интервалом в финансовых операциях является один год, наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечении года после получения ссуды. Известны две основные схемы начисления:

1. Схема простых процентов (simple interest) предполагает неизменность базы, с которой происходит начисление:

Rn = P + P · r + P · r +…+ P · r = P · (1 +n· r)

где Pn – возвращаемая заемщиком сумма; P – сумма основного долга; r – годовая ставка; n – число начислений процентов.

2. Схема сложных процентов (compound interest) предполагает их капитализацию, т. е. база, с которой происходит начисление, посто­янно возрастает на величину начисленных ранее процентов:

к концу первого года: F1 = P + P · r = P·(1 + r)

к концу второго года: F2 = F1 + F1· r = F1·(1 + r)= P ·

…..

к концу n-го года Fn = P·

.

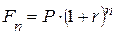Формула алгоритма наращения по схеме сложных процентов может быть представлена следующим образом:

,

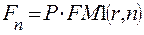где FM 1(r,n) – мультиплицирующий множитель для единичного платежа (проценты начисляются один раз в год).

Как же соотносятся величины Rn и Fn? Это важно знать при проведении финансовых операций. Все зависит от величины n. Сравним множители наращения по простым и сложным процентам, т.е. сравним 1 +n · r и 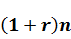. Очевидно, что при n = 1 эти множители совпадают и равны 1+r.

Если 0 < n < 1, то 1 +n · r > 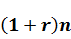, т.е. Rn > Fn.

Если n > 1, то 1 +n · r < 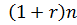, т.е. Rn < Fn.

Графически взаимосвязь Rn и Fn можно представить следующим образом:

Таким образом, в случае ежегодного начисления процентов для лица, предоставляющего кредит:

1) более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);

2) более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);

3) обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.

В случае краткосрочных ссуд со сроком погашения до одного года в качестве показателя n берется величина, характеризующая долю длины подпериода (дни, месяц, квартал, полугодие) в общем периоде (год). Длина различных временных интервалов в расчетах может округляться: месяц– 30 дней, квартал – 90 дней, полугодие – 180 дней, год – 360 (или 365, 366)дней.

Дата добавления: 2014-01-04