Розв'язок диференційного рівняння з метою визначення швидкості осадження

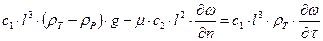
Приведемо рівняння до безрозмірного вигляду. Для цього розділимо всі його частини на

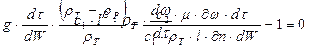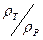
Домножимо всі члени рівняння на безрозмірне співвідношення

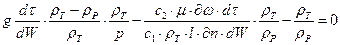(2.2.1)

В кожному доданку викреслюємо символи диференціювання і напрямку (заміна n на неорієнтований в певному напрямку лінійний розмір l).Почнемо з другого члена:

(2.2.2)

де

постійна,яка залежить від форми частинки,і називається коефіцієнтом форми частинки

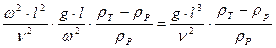
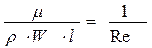(2.2.3)

Безрозмірний комплекс (2.2.3) називають числом Рейнольда.

Він характеризує гідродинаміку потоку і є відношенням інерційних сил до сил тертя. Для зручності використовують обернене значення.

(2.2.4)

Аналогічним шляхом з першого доданку рівняння (2.2.1) отримаємо:

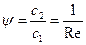(2.2.5)

Домножимо вираз (2.2.4) на Re² і отримаємо число Архімеда:

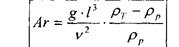(2.2.6)

Воно характеризує відношення різниці сил тяжіння і виштовхуючих до виштовхуючих сили.

Третій доданок рівняння (2.2.1) являє собою параметричний критерій ρ_т/ρ_г враховуючий співвідношення густин твердої частинки і рідини. Оскільки співвідношення густин враховується числом Архімеда, в рівнянні подібності, що описує процес осадження частинки, цей параметричний критерій самостійно звичайно не включають. Крім цього коефіцієнт форми частинки розміщують при числі Архімеда.

Таким чином за допомогою теорії подібності з диференційного рівняння (2.1.4) отримано критеріальне рівняння, що описує процес осадження частинок:

Для практичних розрахунків використовують наступні формули для різних режимів руху частинок:

- ламінарний при Re< 1. 85, YАг < 33

	(2.2.8)

(2.2.9)

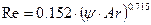-перехідний при 1.85 < Rе <=500, або 33 < YАг<83·10 3

-турбулентний при Rе > 500, або y × Аг > 8× 103

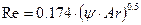(2.2.10)

Дата добавления: 2014-01-04