Программное обеспечение оптимального

По способу получения информации о расположении точки на каждом -ом шаге выделяют методы случайного поиска, направленного (детерминированные) поиска и комбинированные, сочетающие методы случайного и направленного поиска.

Для рассматриваемого класса задач наиболее приемлемы детерминированные методы направленного поиска. Из методов направленного поиска в задачах оптимального проектирования механизмов наиболее широкое применение получили градиентные методы: метод наискорейшего спуска, метод Ньютона, метод сопряженных градиентов и метод переменной метрики [14,15].

Градиентные методы применимы только для непрерывных функций с непрерывными частными производными. Однако выше отмечалось, что целевая функция и ряд функций ограничений вычисляется алгоритмически. Следовательно, при использовании градиентных методов решения задач нелинейного программирования необходимо пользоваться разностными аналогами градиентов целевой функции и функций ограничений. В этом случае, заменяя проекции градиента на 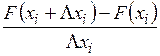для приближенного вычисления градиента в одной точке, необходимо вычислить функцию 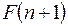раз. В то же время целевая функция и ряд ограничений вычисляются приближенно. Например, приближенно определяется допустимая скорость отскока подпружиненного звена при установке на упор; приближенно вычисляются реакции в кинематических парах с учетом сил трения. Увеличение точности вычислений существенно увеличивает время счета, так как эти функции в процессе поиска оптимальных параметров вычисляются сотни и тысячи раз. Следовательно, задавая произвольное малое приращения -ой компоненте вектора , можно получить приращение 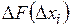, соизмеримое с точностью ее вычисления. Чтобы модуль приращения 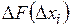был на порядок больше и в то же время достаточно малым, а также чтобы найти производную, следует организовать поиск необходимой величины приращения . В данном случае следует иметь в виду, что при некоторых значениях механизм или кривошип могут не существовать и функция 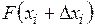может вообще не вычисляться. Таким образом, для вычисления градиента придется обращаться к вычислению функции гораздо больше, чем раз. Все эти вычисления необходимо производить для нахождения одного направления спуска на каждом шаге оптимизации. Это убеждает в целесообразности использования методов минимизации без вычисления производных или, как их еще называют, методов прямого поиска, использующих в процессе поиска минимума функции только информацию о её значении в каждой точке .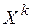

Наиболее простой метод прямого поиска – циклический покоординатный спуск [11] применяется в большинстве случаев в качестве метода начального приближения более точных и эффективных методов, таких как метод Пауэлла [12] или метод сопряженных направлений [13], метод вращающихся координат [11] или модифицированный авторами этот метод и названный как метод по диагонали. В пределах каждой итерации целевая функция является функцией одного переменного . Шаги вдоль направления 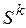делаются с целью определения положения точки минимума целевой функции, так как заранее не известен отрезок, внутри которого лежит эта точка. Для одномерной минимизации применяются следующие методы: метод удвоения шага, метод полиномиальной интерполяции, методы локализации экстремума с использованием числе Фибоначчи, золотого сечения и по методу дихотомии.

Существует несколько методов, позволяющих удовлетворить ограничениям на проектирование при минимизации целевой функции: метод условного градиента, метод проекции градиента, метод возможных направлений, метод последовательной линейной оптимизации и метод штрафных функций. Однако все они, кроме последнего, требуют обязательного вычисления производных целевой функции и функций - ограничений. Основная идея метода штрафных функций [11,13] заключается в том, что задача минимизации целевой функции с ограничениями заменяется последовательностью задач минимизации функции 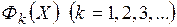без ограничений, где

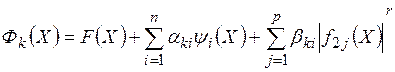, (18)

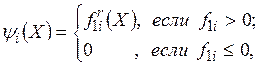
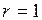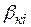или 2. С ростом коэффициенты , увеличиваются, например, удваиваются до тех пор, пока не будут выполнены условия

; ; (19)

,

где - заданные достаточно малые положительные числа.

Если теперь для минимизации (4.24) использовать один из указанных ранее методов прямого поиска, алгоритм поиска оптимальных параметров будет универсальным, то есть не будет зависеть ни от структуры механизма, ни от вида целевой функции и функций ограничений. Однако сходимость этого метода при условии, что ряд функций ограничений вычисляются приближенно, зависит от точности вычисления данных функций и от начальных значений коэффициентов и . Необходимым условием сходимости является невыполнение условий (19) для активных ограничений на первой итерации (при ). Установление значений этих коэффициентов даже в первом приближении является сложной задачей и их выбор полностью ложится на вычислителя. Особенно трудно подобрать значения коэффициентов 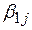. В связи с этим желательно избавляться от ограничений-равенств.

Таким образом, очевидно, что эффективное решение задачи оптимального проектирования механизмов сильно зависит от набора алгоритмов поисковой оптимизации, с которыми знаком конструктор.

На основе анализа существующих методов оптимизации и практики оптимального проектирования машин легкой промышленности предлагается следующий алгоритм поиска оптимальных параметров механизмов:

1) задаются начальные произвольные значения вектору варьируемых параметров ;

2) производится анализ механизма по условиям его существования и вычисления значений функции 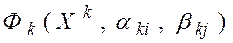при заданных начальных значениях коэффициентов

3) выбирается вектор 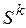и вектору 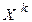по формуле (4.23) присваиваются новые значения 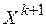и снова вычисляется значение штрафной функции ;

4) осуществляется проверка достижения оптимуму при заданной точности вычисления штрафной функции

;

5) если оптимума нет, то осуществляется переход к пункту 3;

6) осуществляется проверка выполнения поставленных ограничений при заданной точности 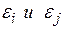вычисления ограничений:

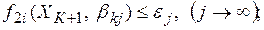
7) если какое-либо из ограничений не выполняется, то значениям присваиваются новые значение и осуществляется переход к пункту 3, или поиск прекращается.

Приведенный алгоритм позволяет находить лишь локальный минимум целевой функции. В этом алгоритме выбор направления движения из точки 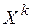в направлении минимума осуществлялся по методу диагонали, адаптированному к задачам оптимального проектирования механизмов. Алгоритм этого метода приведен на рисунках 12 и 13. На рисунке 14 приведен алгоритм покоординатной оптимизации, входящий в состав основного метода как подпрограмма с именем МИНАП. Целевая функция должна быть оформлена как подпрограмма-функция. В одномерном поиске по выбранному направлению использовался алгоритм локализации экстремума по методу дихотомии [15]. Эти алгоритмы оформлены как подпрограммы ДИАГ и МИНАП, инструкции к которым приведены ниже.

Рисунок 12 – Блок-схема подпрограммы оптимизации целевой функции.

Рисунок 13 – Блок-схема алгоритма, реализующего метод покоординатной оптимизации.

. Рисунок 13 – Продолжение

Рисунок 13 –Продолжение.

Рисунок 13 – Продолжение.

Инструкции к подпрограммам оптимизации ДИАГ и МИНАП

ПОДПРОГРАММА ДИАГ (F, C, C1, C2, B, EE, N, e1),

где формальные параметры подпрограммы обозначают:

F – функция-подпрограмма, определяющая целевую функцию;

С(N) – вектор начальных значений переменных (входной вещественный массив);

В(N) – вектор начальных приращений переменных (входной вещественный массив);

С1(N), C2(N), EE(N) – рабочие массивы (входные вещественные массивы);

N – число переменных (целое);

e1 – точность вычисления минимума целевой функции (входная вещественная переменная):

при е1 > 0 – относительная точность вычисления целевой функции;

при е1 < 0 – абсолютная точность вычисления целевой функции.

После работы подпрограммы вектор С(N) содержит значения переменных, соответствующих минимальному значению целевой функции.

ПОДПРОГРАММА МИНАП (F, C, C1, EE, e, FF),

где формальные параметры подпрограммы обозначают:

F, C, C1, EE – то же, что и в подпрограмме ДИАГ;

e - точность вычисления минимума целевой функции (входная вещественная переменная):

при е > 0 – относительная точность вычисления целевой функции;

при е < 0 – абсолютная точность вычисления целевой функции;

FF - значение минимума целевой функции (выходная вещественная переменная).

Дата добавления: 2014-01-04