Partial increments and derivatives of the first order

Let function be defined in a neighborhood of a point 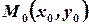and points, belong to this neighborhood too.

Figure 5.1.

Definition 5.1: A difference is called partial increment of the function with respect to 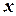and denoted.

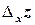Similarly,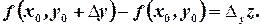

It should be noted, that a ratio can be considered as a function of one variable with respect to and a ratio 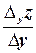- with respect to.

Definition 5.2. The limit of a ratio of partial increment of the function with respect to 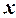to the increment, as tends to zero, is called a partial derivative of function with respect to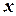

.

Partial derivative with respect to 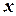of the function can be denoting by one of this ways:

, , .

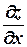By analogy,

.

The partial derivatives and 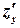are functions of two variables. But when we were finding we assumed that the variable is constant. It means that for finding partial derivatives we can use formulas and theorems for function of the one variable.

Example 5.1. Find partial derivatives of the following functions:

a) , b) .

Solution:

a)

For finding we regard 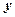as a constant and differentiate with respect to:

;

by analogy,

.

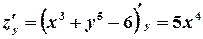b) .

;

.

Дата добавления: 2014-01-04