
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопросы взяты непосредственно из экзаменационных билетов
 |
- Основные кинематические характеристики криволинейного движения: скорость и ускорение. Нормальное и тангенциальное ускорение.
a. Если за равные, сколь угодно малые промежутки времени ∆t частица проходит одинаковый путь ∆s, то такое движение частицы называется равномерным. Разделив путь на время, за которое он пройден, получим величину  , которую назовем скоростью. Однако, если движение было неравномерным, то из этого уравнения мы найдем лишь среднюю скорость. Чтобы найти мгновенную скорость, мы используем следующую формулу:
, которую назовем скоростью. Однако, если движение было неравномерным, то из этого уравнения мы найдем лишь среднюю скорость. Чтобы найти мгновенную скорость, мы используем следующую формулу: 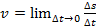 . Так как путь в данном случае выступает в качестве функции от времени имеем ∆S=S(t+∆t)-S(t), а из определения производной получаем
. Так как путь в данном случае выступает в качестве функции от времени имеем ∆S=S(t+∆t)-S(t), а из определения производной получаем 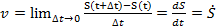 . Если движение не прямолинейно, то компоненты скорости Vx, Vy и Vz равны производным соответствующих координат по времени. Если скорость изменяется со временем равномерно, то величину, характеризующую это изменение, называют ускорением:
. Если движение не прямолинейно, то компоненты скорости Vx, Vy и Vz равны производным соответствующих координат по времени. Если скорость изменяется со временем равномерно, то величину, характеризующую это изменение, называют ускорением: 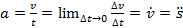 . Пусть
. Пусть 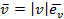 , где
, где  – орт вектор, указывающий направление скорости. При движении по прямой
– орт вектор, указывающий направление скорости. При движении по прямой  При равномерном движении по окружности
При равномерном движении по окружности  ;
; 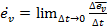 ;
;  – угол, на который сместилась точка,
– угол, на который сместилась точка,  , где n – орт нормали к точке в момент времени t,
, где n – орт нормали к точке в момент времени t, 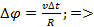
 .
.  – нормальное ускорение, характеризующее скорость поворота вектора скорости, пропорционально модулю скорости и кривизне траектории. При неравномерном движении по криволинейной траектории
– нормальное ускорение, характеризующее скорость поворота вектора скорости, пропорционально модулю скорости и кривизне траектории. При неравномерном движении по криволинейной траектории  ускорение разбивается на два составляющих, одно из которых коллинеарно скорости и, следовательно, направлено по касательной к траектории, его называют тангенциальным
ускорение разбивается на два составляющих, одно из которых коллинеарно скорости и, следовательно, направлено по касательной к траектории, его называют тангенциальным 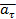 , а второе – нормальное. Так как они перпендикулярны
, а второе – нормальное. Так как они перпендикулярны 
- Кинематика вращательного движения: угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением.
a. Рассмотрим вращательное движение. S=2πRn, где R – радиус окружности, а n – число оборотов. υ= – частота вращения, количество оборотов за единицу времени, T =
– частота вращения, количество оборотов за единицу времени, T = – период вращения, время, за которое точка совершает один полный оборот. Линейная скорость в данном случае находим по следующей формуле:
– период вращения, время, за которое точка совершает один полный оборот. Линейная скорость в данном случае находим по следующей формуле: 
|
|
|
b. Понятие угловая скорость и угловое ускорение относятся к случаю движения материальной точки по окружности. Положение точки М на окружности задается углом φ, который составляет радиус-вектор точки М с неизменным направлением ОХ. Производная этого угла по времени называется угловой скоростью ω:  . Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения в единицу времени, а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Вектор мгновенной скорости тела в этом случае находится, как векторное произведение угловой скорости на радиус, опущенный в точку в которой тело находится:
. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения в единицу времени, а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Вектор мгновенной скорости тела в этом случае находится, как векторное произведение угловой скорости на радиус, опущенный в точку в которой тело находится: 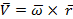 . Угловая скорость же находится по формуле:
. Угловая скорость же находится по формуле: 
c. Первая производная угловой скорости и вторая производная угла по времени – это угловое ускорение: α(альфа). Это так же векторная величина, она со направлена угловой скорости и связана с тангенциальным ускорением: 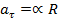 .
.
- Понятие инерциальной системы отсчета. Первый закон Ньютона. Принцип относительности Галилея.
a. Инерциальными называются системы отсчета, в которых тела, не подверженные воздействию других тел, движутся равномерно и прямолинейно. Инерциальной считается гелиоцентрическая система отсчета, в которой начало координат совмещено с солнцем, а координатные оси – с неподвижными звездами. Любая система отсчета, которая движется поступательно, с постоянной скоростью, относительно инерциальной системы отсчета так же является инерциальной.
b. Утверждение о существовании инерциальных систем отсчета Ньютон сформулировал в виде закона инерции, который так же называют первым законом Ньютона: всякое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.
|
|
|
c. Принцип относительности Галилея: если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.
4. Сила. Масса. Второй закон Ньютона. Третий закон Ньютона
a. Сила – это векторная величина, характеризующая воздействие на данное тело со стороны других тел. Модуль этой величины характеризует интенсивность воздействия, а направление совпадает с направлением ускорения, сообщаемого телу данным воздействием. Модуль силы можно определить, например, по растяжению эталонной пружины.
a. В классической механике приходится иметь дело с гравитационными и электромагнитными силами, которые нельзя свести к другим, более простым, силам и поэтому называют фундаментальными.
b. Так же приходится иметь дело с нефундаментальными силами: силой тяжести, имеющей гравитационную природу, силами упругости и трения, имеющими электромагнитную природу.
b. Масса это мера инертности тела, под которой понимают неподатливость тела действию силы, то есть свойство тела противостоять изменению скорости под действием силы. Чтобы определить массу тела, нужно сравнить ее с массой эталонного тела, принятого за единицу.
c. 2-ой закон Ньютона. Произведение массы тела на его скорость назовем импульсом. Второй закон гласит, что скорость изменения импульса частицы равна силе, действующей на нее.
d. 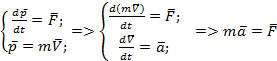 .
.
e. Воздействие тел друг на друга имеет характер взаимодействия и если тело 2 действует на тело 1 с силой F12, то тело 1 так же действует на тело 2 с силой F21. Третий закон Ньютона гласит, что силы, с которыми два тела взаимодействуют, равны по модулю и противоположны по направлению: F12=- F21.
i. Силы действуют вдоль одной прямой,
ii. Они имеют одинаковую природу
iii. Они приложены к различным телам, поэтому не могут уравновесить друг друга.
iv. Третий закон справедлив только для инерциальных систем отсчета.
|
|
|
- Импульс материальной точки и системы материальных точек. Замкнутые системы. Закон сохранения импульса.
a. Импульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:  . Замкнутая система тел в механике — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют.
. Замкнутая система тел в механике — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют.
b. В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:  , а
, а  соответственно называется импульсом точки В релятивистской механике
соответственно называется импульсом точки В релятивистской механике 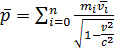
c.. Импульс системы, на которую не действуют никакие внешние силы (или они скомпенсированы), сохраняется во времени согласно второму и третьему законам Ньютона: импульсы всех точек попарно уравновешивают друг друга
импульсы всех точек попарно уравновешивают друг друга 
- Момент импульса материальной точки и твердого тела относительно точки и относительно оси. Момент силы относительно точки и относительно оси. Уравнение моментов.
a. Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости): 
b. Момент импульса (угловой момент) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр. Момент импульса замкнутой системы сохраняется.  , где р – импульс точки, а r – радиус вектор от оси вращения. Момент импульса системы материальных точек равен сумме моментов каждой точки. Момент импульса тела можно найти интегралом
, где р – импульс точки, а r – радиус вектор от оси вращения. Момент импульса системы материальных точек равен сумме моментов каждой точки. Момент импульса тела можно найти интегралом  .
.
|
|
|

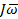
Момент силы (крутящий момент, вращательный момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. 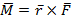 . Вектор, обозначающий момент сил является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться.
. Вектор, обозначающий момент сил является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. 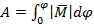 . Как сила является производной от импульса по времени, так и момент силы является производной от момента импульса.
. Как сила является производной от импульса по времени, так и момент силы является производной от момента импульса.  Это уравнение называется уравнением моментов.
Это уравнение называется уравнением моментов.  – это основное уравнение динамики движения твердого тела вокруг закрепленной оси.
– это основное уравнение динамики движения твердого тела вокруг закрепленной оси.
- Уравнение моментов для материальной точки. Момент импульса твердого тела. Момент инерции. Основное уравнение динамики движения твердого тела вокруг закрепленной оси.
a. См. п. 6
- Момент инерции. Формула Штейнера. Кинетическая энергия вращающегося твердого тела.
a. Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости): 
b. Теорема Гюйгенса — Штейнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции J тела относительно произвольной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями 
c.. Кинетическая энергия вращающегося твердого тела находится аналогично кинетической энергии прямолинейного движения: 
- Сила, работа и потенциальная энергия. Консервативные и неконсервативные силы.
a. Сила – это векторная величина, характеризующая воздействие на данное тело со стороны других тел. Модуль этой величины характеризует интенсивность воздействия, а направление совпадает с направлением ускорения, сообщаемого телу данным воздействием. Модуль силы можно определить, например, по растяжению эталонной пружины.
a. В классической механике приходится иметь дело с гравитационными и электромагнитными силами, которые нельзя свести к другим, более простым, силам и поэтому называют фундаментальными.
b. Так же приходится иметь дело с нефундаментальными силами: силой тяжести, имеющей гравитационную природу, силами упругости и трения, имеющими электромагнитную природу.
b. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия сил на тело, зависящая от модуля этих сил от их направления и от перемещения тела. dA=
c. Кинетическая энергия вводится в механике в прямой связи с понятием работы. Схема рассуждений такова:
a. 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины.
b. 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия). A=
d. Консервативные силы (потенциальные силы) — это силы, работа которых не зависит от траектории точки приложения этой силы и закона её движения и определяется только начальным и конечным положением этой точки. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.
e. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примером неконсервативной силы является сила трения.
f. Потенциальная энергия  — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальной точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении. Потенциальная энергия тела
— скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальной точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении. Потенциальная энергия тела  в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:  .
.
g. Пространство, в котором действуют консервативные силы, называется потенциальным полем.
Каждой точке потенциального поля соответствует некоторое значение силы 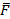 , действующей на тело, и некоторое значение потенциальной энергии
, действующей на тело, и некоторое значение потенциальной энергии  . Значит, между силой
. Значит, между силой 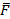 и
и  должна быть связь dA=
должна быть связь dA= , с другой стороны, d A = –d
, с другой стороны, d A = –d , следовательно
, следовательно  , отсюда
, отсюда  .
.
h. Если спроецировать вектор силы на оси координат, получим: 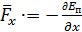 ;
;  ;
;  ; таким образом можно выразить вектор силы через его проекции:
; таким образом можно выразить вектор силы через его проекции:  .
.
i. Градиент – это вектор, показывающий направление наибыстрейшего изменения функции. Следовательно, вектор  направлен в сторону наибыстрейшего уменьшения
направлен в сторону наибыстрейшего уменьшения  .
.
- Консервативные и неконсервативные силы. Сила тяжести как консервативная сила. Потенциальная энергия.
a. Консервативные силы (потенциальные силы) — это силы, работа которых не зависит от траектории точки приложения этой силы и закона её движения и определяется только начальным и конечным положением этой точки. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.
b. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примером неконсервативной силы является сила трения.
c. Потенциальная энергия  — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальной точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении. Потенциальная энергия тела
— скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальной точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении. Потенциальная энергия тела  в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:  .
.
d. Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта.
e. Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени.
f. Рассмотрим в качестве примера задачу с мячом, который подбрасывают с земли. В качестве точки начала отсчета выберем поверхность земли и направим ось измерения вверх. В тот момент, когда он находится на земле h=0 => потенциальная работа так же равна нулю, однако после того, как ему сообщили энергию он поднимается на некоторую высоту h=H, где его потенциальная энергия максимальна, а кинетическая, согласно закону сохранения энергии, равна нулю. После этого, под действием силы тяжести, устремляется вниз, достигает поверхности, где его потенциальная энергия снова равна нулю, а кинетическая, согласно закону сохранения энергии, равна той, которую ему придали в момент запуска. Так как работа равна изменению кинетической энергии, а она в начале и в конце траектории одинакова, работа равна нулю. Так как работа по замкнутому контуру равна нулю, сила тяжести является консервативной.
- Сила упругости как консервативная сила.
a. Работа силы упругости:  , однако, в замкнутой системе под действием силы упругости тело будет возвращаться в исходную точку => ∆x=0 => работа по замкнутому контуру равна нулю, следовательно сила консервативная.
, однако, в замкнутой системе под действием силы упругости тело будет возвращаться в исходную точку => ∆x=0 => работа по замкнутому контуру равна нулю, следовательно сила консервативная.
- Консервативные и неконсервативные силы. Сила гравитации как консервативная сила. Потенциальная энергия.
a. Работа силы гравитации  зависит от изменения положения тела в пространстве
зависит от изменения положения тела в пространстве  , при перемещении по замкнутому контуру
, при перемещении по замкнутому контуру 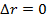 , следовательно работа по замкнутому контуру равна нулю, следовательно сила консервативная.
, следовательно работа по замкнутому контуру равна нулю, следовательно сила консервативная.
13. Связь между силой и потенциальной энергией. Градиент скалярной функции.
a. Смотри пункты 9.a, 9.f-9.i.
- Законы сохранения в классической механике.
a. Импульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:  . Замкнутая система тел в механике — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют. Закон сохранения импульса. В замкнутой системе, в которой на тела действуют только внутренние силы, векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой:
. Замкнутая система тел в механике — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют. Закон сохранения импульса. В замкнутой системе, в которой на тела действуют только внутренние силы, векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой:

b. Закон сохранения импульса можно применить к реактивному движению – движению тела, возникающему в результате выброса им вещества. В применении к движению ракеты ее скорость υ после истечения газов равна  , где u – скорость газов относительно ракеты, M0 – начальная масса ракеты, а M – полезная масса ракеты. Это соотношение называется формулой Циолковского.
, где u – скорость газов относительно ракеты, M0 – начальная масса ракеты, а M – полезная масса ракеты. Это соотношение называется формулой Циолковского.
c. Ракета является примером тела переменной массы. К таким телам можно применять второй закон Ньютона, но ко всем внешним силам, действующим на тело переменной массы, следует добавлять силу реакции вытекающей струи: 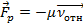 . Здесь νотн – скорость истекающих газов относительно ракеты, μ – масса вещества, истекающего за 1 с. В случае ракеты μ – расход топлива за 1 с:
. Здесь νотн – скорость истекающих газов относительно ракеты, μ – масса вещества, истекающего за 1 с. В случае ракеты μ – расход топлива за 1 с: 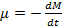 .
.
d. Абсолютно упругим ударом называется столкновение двух тел, в результате которого сохраняется механическая энергия системы тел:  . Если же удар неупругий, то механическая энергия полностью или частично переходит во внутреннюю энергию сталкивающихся тел. В обоих случаях выполняется закон сохранения импульса.
. Если же удар неупругий, то механическая энергия полностью или частично переходит во внутреннюю энергию сталкивающихся тел. В обоих случаях выполняется закон сохранения импульса.
e. Если в системе действуют только потенциальные силы, то справедлив закон сохранения механической энергии: в замкнутой системе сумма кинетической и потенциальной энергии тел остается неизменной: 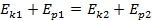 . Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму
. Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму  называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
- Постулаты специальной теории относительности. Основные кинематические следствия СТО. Одновременность событий в СТО.
a. Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, — релятивистскими скоростями. Основным отличием СТО от классической механики является зависимость (наблюдаемых) пространственных и временных характеристик от скорости. Центральное место в специальной теории относительности занимают преобразования Лоренца, которые позволяют преобразовывать пространственно-временные координаты событий при переходе от одной инерциальной системы отсчета к другой.
b. Постулат 1 (принцип относительности Эйнштейна). Любое физическое явление протекает одинаково во всех инерциальных системах отсчёта. Это означает, что форма зависимости физических законов от пространственно-временных координат должна быть одинаковой во всех Инерциальных Системах Отсчета, то есть законы инвариантны относительно переходов между ИСО. Принцип относительности устанавливает равноправие всех ИСО.
c. Постулат 2 (принцип постоянства скорости света). Скорость света в «покоящейся» системе отсчёта не зависит от скорости источника. Поскольку источник имеет разные скорости в разных ИСО, то это означает, что скорость света одинакова во всех инерциальных системах.
d. В СТО постулируется возможность определения единого времени в рамках данной инерциальной системы отсчёта. Для этого вводится процедура синхронизации двух часов, находящихся в различных точках ИСО. Пусть от первых часов в момент времени t1 ко вторым посылается сигнал с постоянной скоростью u. Сразу по достижении вторых часов (по их показаниям в момент времени T) сигнал отправляется обратно с той же постоянной скоростью u и достигает первых часов в момент времени t2. Часы считаются синхронизированными, если выполняется соотношение T=(t1+t2)/2.
e. Если два разнесённых в пространстве события (например, вспышки света) происходят одновременно в движущейся системе отсчёта S', то они будут неодновременны относительно «неподвижной» системы S. При ∆t'=0 из преобразований Лоренца следует 
f. Если длину движущегося объекта определять при помощи одновременной фиксации координат его поверхности, то из преобразований Лоренца следует, что линейные размеры такого тела относительно «неподвижной» системы отсчёта сокращаются: 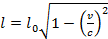 , где l = ∆x— длина вдоль направления движения относительно неподвижной системы отсчёта, а l0 = ∆x' — длина в движущейся системе отсчёта, связанной с телом (т. н. собственная длина тела). При этом сокращаются продольные размеры тела (то есть измеряемые вдоль направления движения). Поперечные размеры не изменяются.
, где l = ∆x— длина вдоль направления движения относительно неподвижной системы отсчёта, а l0 = ∆x' — длина в движущейся системе отсчёта, связанной с телом (т. н. собственная длина тела). При этом сокращаются продольные размеры тела (то есть измеряемые вдоль направления движения). Поперечные размеры не изменяются.
16. Закон Кулона. Напряженность электростатического поля. Принцип суперпозиции.
a. Закон Кулона — это закон, описывающий силы взаимодействия между точечными электрическими зарядами. Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними. 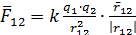 , где
, где 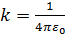 ,
, 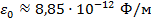
b. Напряжённость электрического поля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 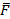 , действующей на неподвижный пробный заряд, помещенный в данную точку поля, к величине этого заряда q:
, действующей на неподвижный пробный заряд, помещенный в данную точку поля, к величине этого заряда q:  , где
, где  - электростатический потенциал. То есть напряженность электростатического поля направлена в сторону скорейшего падения потенциала. Напряженность поля, создаваемая в пространстве точечным зарядом равна:
- электростатический потенциал. То есть напряженность электростатического поля направлена в сторону скорейшего падения потенциала. Напряженность поля, создаваемая в пространстве точечным зарядом равна: 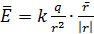 .
.
c. Принцип суперпозиции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит: результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
d. Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.
17. Работа сил электростатического поля при перемещении заряда. Циркуляция вектора напряжённости. Потенциальный характер электростатического поля.
a. 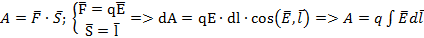
b. Pабота сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q.
c. Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля: .Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.
.Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е. 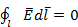 . Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле - потенциальным.
. Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле - потенциальным.
- Электростатическое поле. Напряженность и потенциал электростатического поля. Теорема о циркуляции.
a. Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга.
b. Напряжённость электрического поля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 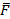 , действующей на неподвижный пробный заряд, помещенный в данную точку поля, к величине этого заряда q:
, действующей на неподвижный пробный заряд, помещенный в данную точку поля, к величине этого заряда q:  , где
, где  - электростатический потенциал. То есть напряженность электростатического поля направлена в сторону скорейшего падения потенциала. Напряженность поля, создаваемая в пространстве точечным зарядом равна:
- электростатический потенциал. То есть напряженность электростатического поля направлена в сторону скорейшего падения потенциала. Напряженность поля, создаваемая в пространстве точечным зарядом равна: 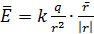 .
.
c. Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля: .Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.
.Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е. 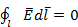 . Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле – потенциальным.
. Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле – потенциальным.
d. Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции. 
- Эквипотенциальные поверхности и силовые линии электростатического поля. Теорема о циркуляции. Безвихревой характер электрического поля.
a. Эквипотенциальные поверхности — понятие, применимое к любому потенциальному векторному полю, например, к статическому электрическому полю. Эквипотенциальная поверхность — это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение, поверхность, в любой своей точке ортогональная силовым линиям поля. Поверхность проводника в электростатике является эквипотенциальной поверхностью. Кроме того, помещение проводника на эквипотенциальную поверхность не вызывает изменения конфигурации электростатического поля. Этот факт используется в методе изображений, который позволяет рассчитывать электростатическое поле для сложных конфигураций.
b. Силовые линии указывают направление силы, действующей на положительный заряд в данной точке поля.
a. Силовые линии электрического поля имеют начало и конец. Они начинаются на положительных зарядах и заканчиваются на отрицательных.
b. Силовые линии электрического поля всегда перпендикулярны поверхности проводника.
c. Распределение силовых линий электрического поля определяет характер поля. Поле может быть радиальным (если силовые линии выходят из одной точки или сходятся в одной точке), однородным (если силовые линии параллельны) и неоднородным (если силовые линии не параллельны).
c. Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля: .Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.
.Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е. 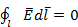 . Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле – потенциальным.
. Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле – потенциальным.
d. Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции. 
e. Из условия  следует, что
следует, что  . Следовательно, кулоновское поле – безвихревое. Следовательно,
. Следовательно, кулоновское поле – безвихревое. Следовательно, 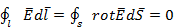 , что еще раз доказывает нам, что работа по перемещению заряда по любому замкнутому контуру равна нулю, а поле потенциально.
, что еще раз доказывает нам, что работа по перемещению заряда по любому замкнутому контуру равна нулю, а поле потенциально.
- Эквипотенциальные поверхности и силовые линии электростатического поля между проводниками. Электростатическая защита.
- Электростатическая защита — помещение приборов, чувствительных к электрическому полю, внутрь замкнутой проводящей оболочки для экранирования от внешнего электрического поля. Это явление связано с тем, что на поверхности проводника (заряженного или незаряженного), помещённого во внешнее электрическое поле, заряды перераспределяются под действием явления электростатической индукции так, что создаваемое ими внутри проводника поле полностью компенсирует внешнее.
21. Емкость проводников и конденсаторов. Энергия заряженного конденсатора.
a. Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.  В Международной системе единиц (СИ) ёмкость измеряется в фарадах. Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):
В Международной системе единиц (СИ) ёмкость измеряется в фарадах. Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ): 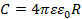 , где
, где  - электрическая постоянная, а
- электрическая постоянная, а 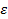 - относительная диэлектрическая проницаемость.
- относительная диэлектрическая проницаемость.
b. Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком или вакуумом, — к конденсатору. В этом случае ёмкость (взаимная ёмкость) этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна: 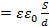 , где S — площадь одной обкладки (подразумевается, что обкладки одинаковы), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды между обкладками, ε0 = 8.854·10−12 Ф/м — электрическая постоянная.
, где S — площадь одной обкладки (подразумевается, что обкладки одинаковы), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды между обкладками, ε0 = 8.854·10−12 Ф/м — электрическая постоянная.
c. Конденсатор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. В простейшем варианте конструкции состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения. Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:
- Диэлектрики. Типы диэлектриков. Поляризация диэлектриков. Свободные и связанные заряды. Влияние диэлектриков на электрическое поле.
a. Диэлектрик (изолятор) — вещество, практически не проводящее электрический ток. Концентрация свободных носителей заряда в диэлектрике не превышает 108 см−3. Основное свойство диэлектрика состоит в способности поляризоваться во внешнем электрическом поле. Условно к проводникам относят материалы с удельным электрическим сопротивлением ρ < 10−5 Ом·м, а к диэлектрикам — материалы, у которых ρ > 108 Ом·м. К диэлектрикам относятся воздух и другие газы, стёкла, различные смолы, пластмассы, многие виды резины. Активными (управляемыми) диэлектриками являются сегнетоэлектрики, пьезоэлектрики, пироэлектрики, электролюминофоры, материалы для излучателей и затворов в лазерной технике, электреты и др.
b. Диэлектрики, как и любые вещества, состоят из атомов и молекул. В целом молекулы нейтральны, тем не менее, они взаимодействуют с электрическим полем. Например, в случае, когда симметрия молекулы отлична от сферической, ее можно представить в виде электрического диполя- идеализированной электронейтральной системы, состоящей из точечных и равных по абсолютной величине положительного и отрицательного электрических зарядов. Электрический дипольный момент молекулы p=ql, где q - суммарный заряд ядер или электронов; l - вектор, представляющий собой плечо эквивалентного диполя.
a. Молекулы, обладающие электрическим дипольным моментом, называют полярными. Полярным диэлектриком является вода;
b. Молекулы, у которых положения эквивалентного положительного и эквивалентного отрицательного заряда совпадают и, следовательно, дипольный момент каждой молекулы равен нулю (p=0), называют неполярными.
c. Третью группу диэлектриков (NaCl, KCl, КВr,...) составляют вещества, молекулы которых имеют ионное строение. Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток. При наложении на ионный кристалл электрического поля происходит некоторая деформация кристаллической решетки или относительное смещение подрешеток, приводящее к возникновению дипольных моментов.
c. Поляризацией диэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей. Соответственно трем группам диэлектриков различают три вида поляризации:
a. электронная, или деформационная, поляризация диэлектрика с неполярными молекулами, заключающаяся в возникновении у атомов индуцированного дипольного момента за счет деформации электронных орбит;
b. ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации имеющихся дипольных моментов молекул по полю. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрическое поле и тепловое движение) возникает преимущественная ориентация дипольных моментов молекул по полю. Эта ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура;
c. ионная поляризация диэлектриков с ионными кристаллическими решетками, заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных — против поля, приводящем к возникновению дипольных моментов.
d. Свободными называются заряды, способные передвигаться по всему телу, на котором они находятся, под действием электрического поля, в которое тело помещено. Связанными называются заряды, входящие состав молекул диэлектриков (изоляторов), которые под действием внешнего электрического поля могут лишь смещаться в пределах молекулы относительно положения равновесия, но покинуть молекулу не могут.
e. Влияние диэлектрика на электрическое поле заключается прежде всего в том, что диэлектрик ослабляет напряженность электрического поля. По обобщенному закону Кулона в однородной диэлектрической среде, имеющей диэлектрическую постоянную ε, электрические заряды взаимодействуют с силой, в n раз меньшей, чем в вакууме.
- Поток вектора через поверхность. Теорема Гаусса в интегральной форме и ее применение для расчета электрического поля равномерно заряженного шара, цилиндра, нити, плоскости.
a. Поток векторного поля через поверхность — поверхностный интеграл второго рода по поверхности S.  .
.
b. По теореме Гаусса поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.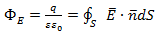 .
.
c. Теорема Гаусса для магнитной индукции гласит: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю: .
.
d. Применение теоремы Гаусса для расчета электрического поля равномерно заряженного шара, цилиндра, нити, плоскости.
a. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью: пусть сферическая поверхность радиуса R несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность заряда δ в любой точке сферы будет одинакова. Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен  . По теореме Гаусса
. По теореме Гаусса  , следовательно
, следовательно  . Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре, следовательно для точек находящихся на поверхности сферы справедливо:
. Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре, следовательно для точек находящихся на поверхности сферы справедливо:  . Внутри сферы Е=0.
. Внутри сферы Е=0.
b. Электростатическое поле шара. Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью ρ>0. В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда 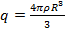 , расположенного в центре шара. Тогда вне шара
, расположенного в центре шара. Тогда вне шара  , а на его поверхности (r=R)
, а на его поверхности (r=R)  . Внутри шара r<R
. Внутри шара r<R  .
.
c. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра). Предположим, что существует полая цилиндрическая поверхность радиуса R, заряженная с постоянной линейной плотностью τ(тау)>0. Проведем соосную цилиндрическую поверхность радиуса r от оси (r>R), поток вектора напряженности через эту поверхность  . По теореме Гаусса
. По теореме Гаусса  , следовательно
, следовательно  .
.
d. Напряженность поля равномерно заряженной бесконечной плоскости. Предположим, что существует бесконечная плоскость, заряженная с постоянной плоскостной плотностью δ>0. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости. Суммарный поток вектора; напряженности равен вектору  , умноженному на площадь S первого основания, плюс поток вектора
, умноженному на площадь S первого основания, плюс поток вектора  через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом,
через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом,  , так как
, так как 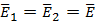 . С другой стороны по теореме Гаусса поток вектора напряженности через эту поверхность
. С другой стороны по теореме Гаусса поток вектора напряженности через эту поверхность  , следовательно
, следовательно  .
.
- Энергия системы неподвижных зарядов. Энергия заряженного проводника и конденсатора. Энергия и объёмная плотность энергии электрического поля.
a. Т.к. электростатические силы взаимодействия консервативны, система зарядов обладает потенциальной энергией.
Потенциальные энергии системы двух неподвижных точечных зарядов Q1 и Q2, находящихся на расстоянии r друг от друга равны  , где
, где  и
и  — соответственно потенциалы,создаваемые зарядом
— соответственно потенциалы,создаваемые зарядом 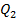 ,в точке нахождения заряда
,в точке нахождения заряда 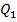 и зарядом
и зарядом 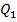 в точке нахождения заряда
в точке нахождения заряда 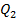 .
.
Потенциалы равны: 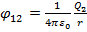 ;
;  , поэтому W1 = W2 = W и
, поэтому W1 = W2 = W и  . Добавляя к нашей системе из двух зарядов последовательно заряды Q3, Q4,..., можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна
. Добавляя к нашей системе из двух зарядов последовательно заряды Q3, Q4,..., можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна  , где φi — потенциал, который создается в точке, где находится заряд Qi, всеми зарядами, кроме i-го.
, где φi — потенциал, который создается в точке, где находится заряд Qi, всеми зарядами, кроме i-го.
b. Энергия заряженного уединенного проводника. Рассмотрим уединенный проводник, заряд, потенциал и емкость которого соответственно равны Q, φ и С. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, при этом затратив на это работу, которая равна  - элементарная работа сил электрического поля заряженного проводника. Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу
- элементарная работа сил электрического поля заряженного проводника. Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу  . Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:
. Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:  (2). Формулу (2) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, то из (1) найдем
(2). Формулу (2) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, то из (1) найдем 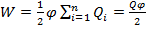 , где Q=∑Qi - заряд проводника.
, где Q=∑Qi - заряд проводника.
c. Энергия заряженного конденсатора. Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы (2) равна  (3), где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора. Используя выражение (3), будем искать механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. Для этого сделаем предположение, что расстояние
(3), где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора. Используя выражение (3), будем искать механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. Для этого сделаем предположение, что расстояние  между пластинами изменилось на величину
между пластинами изменилось на величину 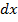 . Тогда действующая сила совершает работу
. Тогда действующая сила совершает работу  вследствие уменьшения потенциальной энергии системы
вследствие уменьшения потенциальной энергии системы  , откуда
, откуда  . Подставив в (3) выражение для емкости плоского конденсатора, получим
. Подставив в (3) выражение для емкости плоского конденсатора, получим  . Продифференцировав при фиксированном значении энергии, получим искомую силу:
. Продифференцировав при фиксированном значении энергии, получим искомую силу: 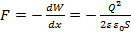 , где знак минус указывает, что сила F является силой притяжения.
, где знак минус указывает, что сила F является силой притяжения.
d. Энергия электростатического поля. Используем выражение (3), которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, и пользуяcь выражением для емкости плоского конденсатора ( ) и разности потенциалов между его обкладками (
) и разности потенциалов между его обкладками ( ). Тогда
). Тогда  (4), где V= Sd — объем конденсатора. Формула (4) говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е.
(4), где V= Sd — объем конденсатора. Формула (4) говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е.
e. Объемная плотность энергии электростатического поля (энергия единицы объема)  (5). Выражение (5) справедливо только для изотропного диэлектрика, для которого выполняется соотношение:
(5). Выражение (5) справедливо только для изотропного диэлектрика, для которого выполняется соотношение: 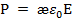 . Формулы (3) и (4) соответственно выражают энергию конденсатора через заряд на его обкладках и через напряженность поля.
. Формулы (3) и (4) соответственно выражают энергию конденсатора через заряд на его обкладках и через напряженность поля.
- Электрический ток. Сила тока. Плотность тока. Условия существования постоянного тока. Обобщённый закон Ома в интегральной форме. Разность потенциалов, напряжение, ЭДС. Закон Джоуля – Ленца.
a. Электрический ток — направленное движение заряженных частиц. Электрический ток имеет следующие проявления:
i. Нагревание проводников (в сверхпроводниках не происходит выделения теплоты).
ii. Изменение химического состава проводников (наблюдается преимущественно в электролитах).
iii. Создание магнитного поля (проявляется у всех без исключения проводников).
Различают переменный и постоянный электрические токи.
Постоянный ток — ток, направление и величина которого слабо меняются во времени.
Переменный ток — ток, величина и направление которого меняются во времени. В широком смысле под переменным током понимают любой ток, не являющийся постоянным.
Электрический ток имеет количественные характеристики: скалярную — силу тока, и векторную — плотность тока.
b. Сила тока — это физическая величина, равная отношению количества заряда, прошедшего за некоторое время через поперечное сечение проводника, к величине этого промежутка времени. По закону Ома сила тока  на участке цепи прямо пропорциональна напряжению
на участке цепи прямо пропорциональна напряжению  , приложенному к этому участку цепи, и обратно пропорциональна его сопротивлению
, приложенному к этому участку цепи, и обратно пропорциональна его сопротивлению 
 .
.
Если на участке цепи электрический ток не постоянный, то напряжение и сила тока постоянно изменяется, при этом у обычного переменного тока среднее значения напряжения и силы тока равны нулю. Однако средняя мощность выделяемого при этом тепла нулю не равна. Поэтому применяют следующие понятия:
i. мгновенные напряжение и сила тока, то есть действующие в данный момент времени.
ii. амплитудные напряжение и сила тока, то есть максимальные абсолютные значения
iii. эффективные (действующие) напряжение и сила тока определяются тепловым действием тока, то есть имеют те же значения, которые они имеют у постоянного тока с таким же тепловым эффектом.
c. Плотность тока — это вектор, абсолютная величина которого равна отношению силы тока, протекающего через некоторое сечение проводника, перпендикулярное направлению тока, к площади этого сечения, а направление вектора совпадает с направлением движения положительных зарядов, образующих ток. Согласно закону Ома в дифференциальной форме плотность тока в среде пропорциональна напряжённости электрического поля
пропорциональна напряжённости электрического поля  и проводимости среды σ:
и проводимости среды σ: 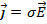 .
.
d. Условия возникновения и существования постоянного электрического тока:
i. наличие свободных заряженных частиц;
ii. на заряженные частицы должны действовать силы, обеспечивающие их упорядоченное перемещение в течение конечного промежутка времени.
Для того чтобы в проводнике мог существовать постоянный ток проводимости, необходимо выполнение следующих условий:
iii. напряженность электрического поля в проводнике должна быть отлична от нуля и не должна изменяться с течением времени;
iv. цепь постоянного тока проводимости должна быть замкнутой;
v. на свободные электрические заряды, помимо кулоновских сил, должны действовать неэлектростатические силы, называемые сторонними силами. Сторонние силы могут быть созданы источниками тока (гальваническими элементами, аккумуляторами, электрическими генераторами и др.).
e. Участок цепи, на котором не действуют сторонние силы, называется однородным. Участок цепи, на котором действуют сторонние силы, называется неоднородным. В общем случае на неоднородном участке цепи действуют и кулоновские и сторонние силы. Обозначим напряженность поля электростатических (кулоновских) сил через Ек, а напряженность поля сторонних сил через Естор. Тогда в любой точке внутри проводника результирующая напряженность равна
 (1). Так как сила постоянного тока во всех сечениях проводника постоянна, то сила тока вынесена за знак интеграла.
(1). Так как сила постоянного тока во всех сечениях проводника постоянна, то сила тока вынесена за знак интеграла.
f. Первый интеграл правой части формулы (1) выражает работу сил электростатического поля по перемещению единичного положительного заряда из точки с потенциалом φ1 в точку с потенциалом φ2. Эта работа в электростатике была названа разностью потенциалов, поэтому 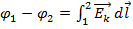 . Второй интеграл правой части формулы (1) выражает работу сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи. Указанная работа сторонних сил называется электродвижущей силой (ЭДС) и часто обозначается символом ε:
. Второй интеграл правой части формулы (1) выражает работу сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи. Указанная работа сторонних сил называется электродвижущей силой (ЭДС) и часто обозначается символом ε:  . ЭДС на участке цепи называется физическая величина, численно равная работе сторонних сил по перемещению единичного положительного заряда на этом участке.
. ЭДС на участке цепи называется физическая величина, численно равная работе сторонних сил по перемещению единичного положительного заряда на этом участке.
g. Закон Джоуля — Ленца: Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля. Математически может быть выражен в следующей форме: 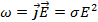 , где ω— мощность выделения тепла в единице объёма,
, где ω— мощность выделения тепла в единице объёма,  — плотность электрического тока,
— плотность электрического тока,  — напряжённость электрического поля, σ — проводимость среды. Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах:
— напряжённость электрического поля, σ — проводимость среды. Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах: 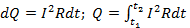 , где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:
, где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:  .
.
26.Вектор магнитной индукции. Закон Ампера. Сила Лоренца.
a. Магнитная индукция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой  магнитное поле действует на заряд
магнитное поле действует на заряд 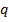 , движущийся со скоростью
, движущийся со скоростью  . Более конкретно,
. Более конкретно,  — это такой вектор, что сила Лоренца
— это такой вектор, что сила Лоренца  , действующая со стороны магнитного поля на заряд
, действующая со стороны магнитного поля на заряд 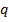 , движущийся со скоростью
, движущийся со скоростью  , равна
, равна  ;
;  , где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика). Вектор магнитной индукции (
, где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика). Вектор магнитной индукции ( ) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции. Измеряется в Теслах
) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции. Измеряется в Теслах  . 1Тл равняется магнитной индукции однородного поля, в котором на плоский контур с током, который имеет магнитный момент 1А*м2 действует max вращающий момент, равный 1 Н*м. на контур с током, помещенный в магнитное поле с индукцией
. 1Тл равняется магнитной индукции однородного поля, в котором на плоский контур с током, который имеет магнитный момент 1А*м2 действует max вращающий момент, равный 1 Н*м. на контур с током, помещенный в магнитное поле с индукцией 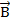 , действует вращательный момент
, действует вращательный момент  , т.е.
, т.е.  , и если
, и если  , то
, то  , при
, при  ,
, 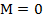 . Это значит, что магнитный момент контура с током зависит от направления вектора магнитной индукции.
. Это значит, что магнитный момент контура с током зависит от направления вектора магнитной индукции.
b. Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. 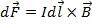 , Idl - элемент тока, где dl – вектор, совпадающий с элементом участка тока и направленный в сторону, в которую течет ток. Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:
, Idl - элемент тока, где dl – вектор, совпадающий с элементом участка тока и направленный в сторону, в которую течет ток. Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:  — закон Ампера. Направление силы Ампера определяется по правилу левой руки. Из закона Ампера виден физический смысл магнитной индукции-величина, численно равная силе, с которой магнитное поле действует на проводник единичной длины, по которому течет единичный ток
— закон Ампера. Направление силы Ампера определяется по правилу левой руки. Из закона Ампера виден физический смысл магнитной индукции-величина, численно равная силе, с которой магнитное поле действует на проводник единичной длины, по которому течет единичный ток  .
.
c. Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:  (1), где q-заряд, v-скорость направленного движения, n-концентрация, N- число зарядов в проводнике длиной l, т.к. dv=Sdl.
(1), где q-заряд, v-скорость направленного движения, n-концентрация, N- число зарядов в проводнике длиной l, т.к. dv=Sdl.  . Тогда, используя закон Ампера:
. Тогда, используя закон Ампера:  , отсюда сила действия на один заряд-(1). Угол α в этом выражении равен углу между скоростью
, отсюда сила действия на один заряд-(1). Угол α в этом выражении равен углу между скоростью