
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифракция Френеля. Метод зон Френеля. Дифракция на круглых отверстиях и экранах
 |
Дифра́кция Френе́ля — дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.
Метод зон Френеля Френель предложил метод разбиения фронта волны на кольцевые зоны, который впоследствии получил название метод зон Френеля.
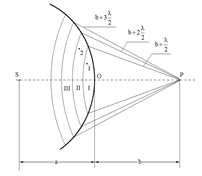
Пусть от источника света S распространяется монохроматическая сферическая волна, P - точка наблюдения. Через точку O проходит сферическая волновая поверхность. Она симметрична относительно прямой SP.
Разобьем эту поверхность на кольцевые зоны I, II, III и т.д. так, чтобы расстояния от краев зоны до точки P отличались на l/2 - половину длины световой волны. Это разбиение было предложено O. Френелем и зоны называют зонами Френеля.
Возьмем произвольную точку 1 в первой зоне Френеля. В зоне II найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку P от точек 1 и 2 будет равна l/2. Вследствие этого колебания от точек 1 и 2 погасят друг друга в точке P.
Из геометрических соображениях следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P от зоны с номером m, уменьшается с ростом m, т.е.
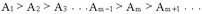
Любые препятствия, находящиеся на пути распространения световой волны, будут закрывать часть зон Френеля на падающем на них
волновом фронте. Поэтому интенсивность прошедшего через них света можно определить, суммируя вклад оставшихся открытыми зон
Френеля.
Если радиус отверстия окажется равным радиусу четной зоны Френеля для точки P, т.е. 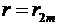 , то вклады четного числа зон компенсируют друг друга, и в точке P освещенность будет минимальна (
, то вклады четного числа зон компенсируют друг друга, и в точке P освещенность будет минимальна (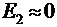 ). Если же в отверстии окажется нечетное число зон Френеля, то освещенность в точке P максимальна:
). Если же в отверстии окажется нечетное число зон Френеля, то освещенность в точке P максимальна:

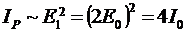 - в 4 раза больше, чем при отсутствии препятствия!
- в 4 раза больше, чем при отсутствии препятствия!
|
|
|
Пусть теперь препятствие (диск) закрывает первые m зон Френеля, тогда для точки P экрана остаются открытыми все остальные зоны, и освещенность в центре экрана по-прежнему не равна нулю: 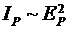 .
.
Все это и объясняет парадоксальные результаты опытов Френеля.
Зонная пластинка. Каким-либо образом, например, лучом лазера, на стеклянной пластинке делаются непрозрачными все четные зоны Френеля (конечно, для какой-то определенной точки наблюдения P). Тогда свет проходит через оставшиеся нечетные зоны "в фазе", и поэтому освещенность в точке P возрастает до значения
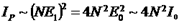 , где N - число зачерненных четных зон Френеля. Такая зонная пластин - ка «фокусирует» лучи в точке P, т.е. может служить в качестве хорошей линзы, причем – широкофокусной!
, где N - число зачерненных четных зон Френеля. Такая зонная пластин - ка «фокусирует» лучи в точке P, т.е. может служить в качестве хорошей линзы, причем – широкофокусной!
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1872; Нарушение авторских прав?; Мы поможем в написании вашей работы!