Основы векторного анализа

Реальные газы, жидкости и кристаллы

Силы межмолекулярного взаимодействия. Реальные газы. Уравнение Ван-дер-Ваальса. Переход из газообразного состояния в жидкое. Критические параметры. Представления о структуре жидкостей, ближнем порядке, радиальной функции распределения. Твердые тела. Ближний и дальний порядок в расположении атомов. Кристаллические решетки. Фазовые переходы между агрегатными состояниями вещества. Фазовые переходы 1 и 2 рода. - 4 часа.

Для описания различных полевых моделей будь то силовое поле или поле скорости жидкости, необходимо использовать особый математический аппарат получившего название векторного анализа. Наибольшую наглядность величины используемые в векторном анализе имеют в случае поля скорости текущей жидкости так как данное поле наиболее наглядно. Предполагаем что имеет место течение идеальной не сжимаемой жидкости с некоторой скоростью 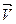в этом случае в той области пространства, где имеет место данное течение жидкости можно определить векторное поле характеризуемое вектором 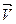. Определим объём протекающий в единицу времени через некоторую поверхность S. Данный объём получил название потока жидкости через поверхность S или переходя от гидродинамического названия к терминам векторного анализа потока вектора 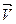через поверхность S.

Для определения данного потока разобьём поверхность S на элементарные площадки dS и определим элементарный поток через данную элементарную площадку. Элементарный объём жидкости прошедший через dS за время dt может быть определён

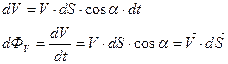
Где: α – угол между нормалью к данной dS и вектором 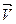; 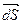- вектор совпадающий по направлению с направлением нормали к элементарной площадке, а длинна этого вектора равна по величине элементарной площадке dS.

Для определения потока через поверхность S просуммируем все элементарные потоки по площадке dS. Реально суммирование сводится к интегрированию по S.

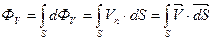
Таким образом мы ввели оператор векторного анализа получившего название потока вектора 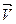через поверхность S.

Аналогично вводим поток любого вектора 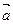векторного поля вектора .

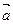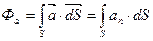
Данный оператор является интегральным оператором векторного анализа. Он описывает поведение векторного поля в некоторой макро области пространства. Поток является скалярной величиной. В векторном анализе вводится понятие потока через замкнутую поверхность. Замкнутой называется поверхность которая содержит в нутрии себя объём.

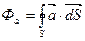
В зависимости от взаимного расположения вектора векторного поля и нормали к элементарной площадке. Элементарный поток может принимать либо положительные либо отрицательные значения. В том случае если угол между вектором 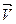и n острый, то поток положительный, если тупой то отрицательный. В случае замкнутой поверхности в качестве положительной нормали к поверхности S принято считать нормаль направленную наружу от объёма находящегося в нутрии замкнутой поверхности.

Введём дифференциальный оператор векторного анализа. Он описывает векторное поле в некоторой точке пространства, где данное поле существует. Предполагаем, что определяем векторное поле вектора текущей идеальной не сжимаемой жидкости 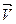. Выбираем некоторую точку Р, а в окрестности данной точки Р определяем замкнутую поверхность S.

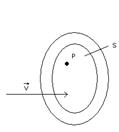
В том случае если поток через данную замкнутую поверхность S будет равен нулю, то следовательно в нутрии данной замкнутой поверхности нет ни источников ни стоков жидкости. В том случае если суммарный поток через данную замкнутую поверхность S является отрицательным, то суммарная мощность стоков превосходит суммарную мощность источников находящихся в нутрии данной замкнутой поверхности S. В этом случае, если поток положительный, то мощность источников превосходит суммарную мощность стоков. Для определения мощности источников, стоков внутри замкнутой поверхности S (В любой точке объема находящейся в нутрии поверхности S) поступим следующим образом: устремим данный объём к точке.

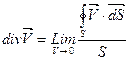
Величина равная отношению потока через замкнутую поверхность S к объёму V находящемуся в нутрии данной замкнутой поверхности при 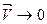получило название дивергенции вектора.

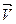Таким образом ввели дифференциальный оператор векторного анализа получивший название дивергенции.

Аналогично можно ввести div для любого другого поля например .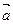

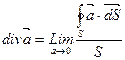
Это оператор векторного анализа который применяется к вектору в результате получаем скалярную величину.

Определяет удельную мощность источников и стоков находящихся внутри V охваченного S.

В декартовой системе координат:

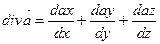
Зная поведение функции дивергенции некоторого векторного поля в каждой точке объёма V находящегося в нутрии замкнутой поверхности S можно определить поток данного векторного поля через поверхность S. Для этого можно воспользоваться теоремой Остроградского Гаусса.

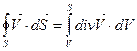
Поток вектора 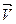через S равен объёмному интегралу от дивергенции по объёму V который находится в нутрии замкнутой поверхности S.

Введём оператор векторного анализа циркуляцию. Обратимся к течению идеальной не сжимаемой идеальной жидкости. Предполагаем что над данной жидкостью выполняются следующие операции.

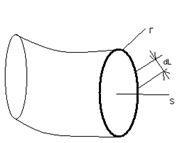
Предполагаем, что ток жидкости замораживаем во всей области пространства кроме бесконечно тонкого контура Г, который охватывает поперечное сечение трубки тока S.

Для того, что бы описать подобное течение жидкости удобно ввести оператор циркуляция вектора 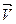по некоторому элементарному контуру длинной dL.

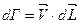- Элементарная циркуляция.

Где: dL – элемент контура. Его направление определяется направлением циркуляции, которое может быть выбрано произвольно. При данном замораживании предполагаем что у вектора скорости отсутствует нормальные по отношению к контуру составляющие и имеются лишь тангенциальные по отношению к контуру составляющие скорости.

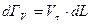
Для определения циркуляции по замкнутому контуру длинной L мы должны сложить все элементарные циркуляции и получаем.

(*)

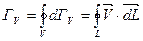Циркуляция является интегральным оператором векторного анализа и описывает поведение векторного поля в некоторой макро области пространства.

Циркуляция является аддитивной величиной это значит что если имеется некоторая поверхность S которая охватывает замкнутый контур Г и внутри этой поверхности имеется несколько поверхностей причём S1 охватывает Г1, а S2 охватывает Г2. Длинна первого L1 длинна второго L2. S=S1+S2, то

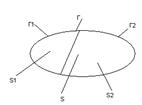
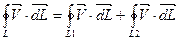
Из аддитивности циркуляции следует, что можно ввести понятие удельной циркуляции, то есть циркуляции в некоторой точке поверхности которая охвачена замкнутым контуром по которому идёт циркуляция. Удельная циркуляция вводится подобно тому как вводится дивергенция, то есть устремим поверхность S охваченную замкнутым контуром L к нулю и найдём отношение циркуляции к поверхности S, но данная характеристика не будет исчерпывающей характеристикой поля так как величина данной циркуляции зависит не только от величины самой циркуляции и поверхности S, но и от ориентации контура по которому идёт циркуляция в пространстве. Ориентацию контура в пространстве можно однозначно определить с помощью положительной нормали к данному контуру которая связана с направлением обхода циркуляции, правилом правого винта.

В качестве характеристики определяющей циркуляцию в некоторой точке пространства удобно использовать векторную величину получившую название |rot|. Это вектор направление которого совпадает с направлением нормали к поверхности которую охватывает замкнутый контур с циркуляцией данного векторного поля, причём при данном направлении нормали величина определяемая формулой (*) имеет максимальное значение, а модуль вектора |rot| определяется как:

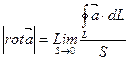(max)

В декартовой системе координат:

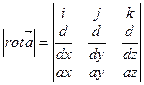
В результате его действия на вектор получается вектор.

Зная поведение функции |rot| на некоторой поверхности S которая охвачена замкнутым контуром L, можно используя известное соотношение векторного анализа, формулу Стокса определить циркуляцию вектора по замкнутому контуру охватывающему поверхность.

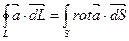- Формула Стокса

Циркуляция вектора 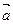по L равно потоку от rot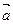через поверхность S которую охватывает контур L.

Оператор Гамильтона (Гамильтониан или оператор Набла). Для более компактной записи операторов векторного анализа удобно использовать гамильтониан который обозначается буквой (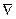). Сам по себе данный оператор не имеет смысла, но приобретает смысл при воздействии на вектор или скалярную функцию.

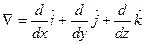Является векторной величиной.

Оператор grad является оператором векторного анализа при воздействии которого на скалярную функцию мА получаем векторную функцию. Grad – это вектор направленный в сторону наибольшего изменения скалярной функции φ.

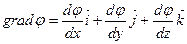
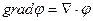
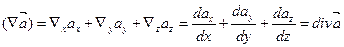
Оператор 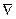можно векторно помножить на .

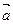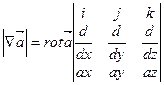
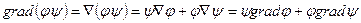
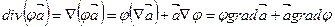
С помощью 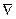удобно раскрывать выражения в которых фигурирует сразу несколько операторов векторного анализа.

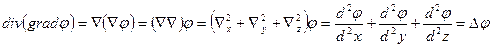
Получили двойную наблу или оператор Лапласа (Лапласиан)

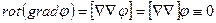
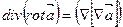
Смешанное произведение которое фигурирует в данном выражении равно объёму параллелепипеда построенного на векторах. В том случае если два вектора совпадают обём параллелепипеда равен нулю, то 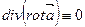Раскрываем по правилу (БАЦ-ЦАБ)

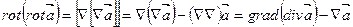
Дата добавления: 2013-12-12