Криволинейные ортогональные системы координат

При описании многих физических процессов удобно использовать криволинейные системы координат (не декартовы). Так как при описании тел цилиндрической формы удобней использовать цилиндрическую систему координат и сферическую которые строятся на основе декартовой системы координат.

Цилиндрическая система может быть получена на основе декартовой следующим образом. Предположим, что есть некоторая точка определённая в декартовой системе координат. Построим цилиндр таким образом что бы основание цилиндра лежало в плоскости XOY декартовой системы координат, на основании которой строим, а точка Р на боковой поверхности данного цилиндра.

Спроецируем точку Р на плоскость XOY и поведем радиус вектор r из точки О который является началом как декартовой системы координат, так и цилиндрической, в точку Р’ являющейся проекцией точки Р на плоскость XOY. Таким образом получим первую координату цилиндрической системы координат (радиус r). Угол между OX и r (Ө). Таким образом мы получили вторую координату цилиндрической системы координат. Ось Z определяет третью координату цилиндрической системы координат. (r, Ө, Z) – координаты в цилиндрической системе координат.

Определим орты данной криволинейной системы координат. Для этого сделаем сечение цилиндра плоскостью параллельной XOY и пересечение данной плоскости и поверхности цилиндра дает нам окружность. Проведём из точки Р единичный вектор 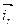который параллелен r. Этот орт будет являться первой координатой r. Проведём единичный отрезок касающийся полученной окружности из точки Р в сторону увеличения Ө. - является второй координатой. Третьим ортом будет являться отрезок 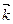- являющийся единичны ортом оси Z.

Сферическая система координат:

Строится на основе декартовой системы координат. Предполагаем что некоторая точка определена в декартовой системе координат, построим некоторую сферическую поверхность так что бы искомая точка лежала на данной поверхности. Проведём радиус вектор r из точки О в точку Р и таким образом мы определим первую координату (r). Угол отсечённый от OZ между осью OZ декартовой системы координат на основании которой строится сферическая и вектором r назовем (α) является второй координатой. Спроецируем точку Р на плоскость XOY получим Р’. Проведём из точки О в точку Р’ луч угол между осью OX и данным лучом отсчитанным от OX определённый как 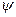является третьей координатой сферической системы координат.

Получим орты данной ортогональной криволинейной системы координат. Для этого выполним сечение данной сферической поверхности плоскостью проходящей через точку Р и осьOZ. Пресечение данной плоскости и поверхности сферы даст нам окружность. Из точки Р отложим единичный вектор 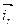сонаправленный с r. Это орт будет первой координатой сферической системы координат. Из точки Р отложим единичный вектор касающийся полученной окружности и направленный в сторону увеличения α – второй орт. Для получения третьего орта сделаем сечение плоскостью параллельной XOY и проходящей через точку Р. Пересечение данной плоскости со сферой даст нам окружность. Отложим единичный вектор касающийся данной окружности и направим в сторону увеличения .

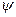Дата добавления: 2013-12-12