Решение дифференциального уравнения свободных затухающих колебаний

Найдём решение дифференциального уравнения свободных затухающих электрических колебаний. Решением уравнения (3).

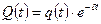(4)

Найдём первую и вторую производные от функции 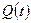с учётом её представления в виде (4)

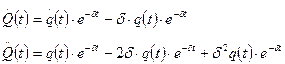
Полученное уравнение подставим в выражение (3)

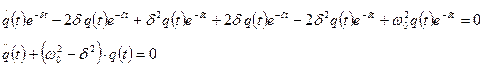
Данное уравнение по форме совпадает с уравнением (*), то есть с уравнением свободных колебаний. Следовательно решением данного уравнения является:

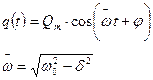
Учитывая что первоначальное решение:

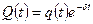
Получаем что решение дифференциального уравнения свободных затухающих колебаний:

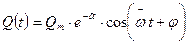
Полученное выражение даёт возможность построить график свободных затухающих колебаний.

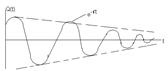
Таким образом из выражения описывающего свободные затухающие колебания следует что амплитуда этих колебаний с течением времени будет изменяться по экспоненциальному закону. Затухающие колебания периодическими не являются, но при малых затуханиях

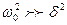
Данное колебание можно считать почти периодическим. При этом под периодом данных колебаний понимают временной интервал между соседними максимумами и минимумами.

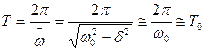
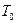- период собственных электрических колебаний.

Данное равенство справедливо для малых затуханий. В качестве характерного колебания вводится величина – дикримент.

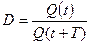
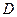- дикримент.

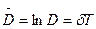
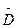- логарифмический дикримент затухания.

В качестве характеристики колебательного контура вводится величина называемая добротностью и обозначается 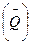. В самом общем случае добротность может определяться как отношение запасённой в колебательном контуре к энергии потерь. Можно показать что между добротностью и логарифмическим дикриментом затухания 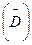существует следующая взаимосвязь

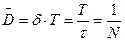
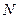- число колебаний через которое амплитуда колебания уменьшается в 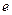раз.

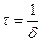- время релаксации (время за которое амплитуда колебаний уменьшается в 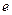раз)

При малых затуханиях

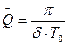
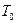- период собственных электрических колебаний, учитывая что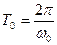

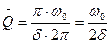
Из полученного выражения добротность обратно пропорциональна коэффициенту затухания.

Дата добавления: 2013-12-12