Электромагнитные волны

Лекция 3.3.

Волновое уравнение для электромагнитного поля.

Уравнения Максвелла для векторов 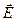и 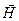можно переписать в виде системы для проекций этих векторов на оси декартовой системы координат

;

(3.3.1)

;

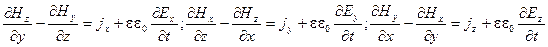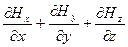=0.

В нейтральной однородной непроводящей среде, где плотность зарядов и плотность тока проводимости равны нулю, уравнения Максвелла запишутся

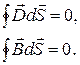(3.3.2)

Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно – без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Это подтверждается тем, что, проведя ряд преобразований с уравнениями (3.3.2), можно получить уравнения , (3.3.3)

.

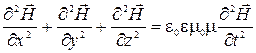Как видно, это волновые уравнения. Они неразрывно связаны друг с другом, так как они получены из (3.3.2), которые связывают вектора и . Они описывают волну векторов и , распространяющуюся с фазовой скоростью

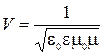. (3.3.4)

В вакууме и скорость электромагнитной волны (скорость света в вакууме) 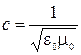. (3.3.5)

Это одна из фундаментальных физических констант. Тогда скорость волны в среде , (3.3.6)

где n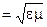 – показатель преломления среды, который определяет во сколько раз скорость электромагнитной волны в среде меньше, чем в вакууме.

Свойства электромагнитных волн.

Установим основные свойства электромагнитной волны на примере плоской волны, распространяющейся в свободном пространстве (отсутствуют заряды и токи).

1. Направим ось х перпендикулярно волновым поверхностям. При этом 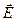и 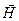, а значит и их проек­ции на оси y и z, не будут зависеть от координат y и z, т. е. со­ответствующие производные по y и z будут равны нулю. Поэто­му уравнения (3.3.1) упрощаются (останутся только про­изводные по x) и принимают вид:

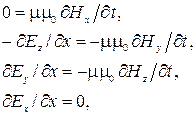
(3.3.7)

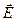Из условий и следует, что E_x не зависит ни от x, ни от t, аналогично - для H_x. Это значит, что отличные от нуля E_x и H_x могут быть обусловлены лишь постоянными однородными полями, накладывающимися на поле волны. А для переменного поля плоской волны E_x = 0 и H_x = 0, т.е. векторы и 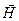перпендикулярны направлению распространения волны – оси x. Значит, электромагнитная волна является поперечной.

2. Кроме того, оказывается, векторы 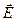и 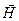в электромагнитной волне взаимно ортогональны. Чтобы убедиться в этом, объединим средние уравнения (3.3.7), содержащие, например, E_y и H_z, в пару:

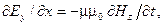
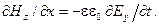(3.3.8)

(можно было бы взять и другую пару, содержащую производные E_z и H_y). Из этих уравнений видно, что изменение во времени, скажем, магнитного поля, направленного вдоль оси z, порожда­ет электрическое поле E_y вдоль оси y. Изменение во времени поля E_y в свою очередь порождает поле H_z и т. д. Ни поля E_z, ни поля H_y при этом не возникает. А это и значит, что ^ .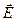

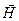3. 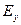и 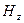являются решениями уравнений

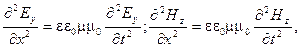(3.3.9)

т.е. представляют собой гармонические функции

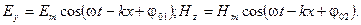(3.3.10)

Как видно из (3.3.9) частоты и волновые числа в этих выражениях одинаковы, отличаются лишь амплитуды и начальные фазы. Подставив эти решения в уравнения (3.3.8), получим

(3.3.11)

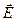Чтобы эти уравнения удовлетворялись в любой момент времени в любой точке пространства, нужно, чтобы . Таким образом колебания векторов и 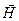в бегущей волне совпадают по фазе. Это значит, что E_y и H_z одинаковы в каждый момент по знаку, одновременно обращаются в нуль и одновременно достигают максимума, что представлено на рис 3.3.1, который называется мгновенным снимком волны.

4. Найдем связь мгновенных значений Ε и Н. Рис.3.3.1.

Поскольку , соотношения (3.3.11) перепишутся

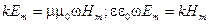. (3.3.12)

Перемножив эти два равенства, получим

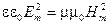. (3.3.13)

Это соотношение связывает амплитуды колебаний Е и Н. Но поскольку фазы их колебаний совпадают, то мгновенные значения подчиняются такому же равенству

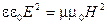
(3.3.14)

Энергия электромагнитной волны. Вектор Пойнтинга.

С бегущей электромагнитной волной связан перенос энергии. Плот­ность потока энергии в этом случае можно найти как и для упругой волны через произведение плотности энергии w на скорость волны V (см.формулу (3.2.23)).

В обычной изотропной среде с проницаемостями ε и μ плот­ность энергии электромагнитного поля равна сумме плотностей энергии электрического и магнитного полей:

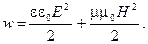(3.3.15)

В данной среде справедливо соотношение (3.3.14) между Ε и Н, а это означает, что плотность электрической составляющей в бегущей волне равна плотности магнитной. Поэтому (3.3.15) мож­но записать так:

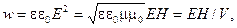(3.3.16)

где V – скорость волны.

Умножив w на V, получим модуль вектора плотности потока энергии:

(3.3.17)

Векторы 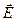и 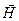взаимно ортогональны и образуют с направ­лением распространения волны правовинтовую систему. Зна­чит, направление вектора их векторного произведения совпадает с направлением пере­носа энергии, а модуль этого вектора равен ЕН. Поэтому век­тор плотности потока электромагнитной энергии 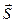можно представить как

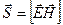. (3.3.18)

Вектор плотности потока энергии электромагнитной волны 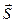называют вектором Пойнтинга.

В случае бегущей гармонической электромагнитной волны (3.3.10) плотность энергии, согласно (3.3.16) и (3.3.14), равна

Плотность же потока энергии, как следует из (3.3.17),

(3.3.19)

где учтено, что скорость V определяется формулой (3.3.4).

Интенсивность I такой волны равна, по определению, сред­нему значению модуля плотности потока энергии: I = < S >. Принимая во внимание, что при усреднении (3.3.19) среднее значение квадра­та косинуса равно 1/2, получим

(3.3.25)

Домножив и поделив подкоренное выражение в этой формуле на 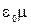и учтя (3.3.5) и (3.3.6), получим

,

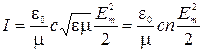или для волны, распространяющейся не ферромагнитной среде (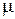мало отличается от единицы) 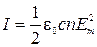(3.3.27)

Обратим внимание, что I пропорционально квадрату амплиту­ды, I ~ Е_m². Необходимо отметить также, что интенсивность электромагнитной волны выражают обычно через напряженность ее электрической составляющей, поскольку, как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света обусловлены именно ею.

Дата добавления: 2013-12-13