
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклади. 1. Розглянемо на площині деяку точку та відкладемо від неї вектори довільного базису
|
|
|
|
1. Розглянемо на площині деяку точку 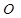 та відкладемо від неї вектори
та відкладемо від неї вектори  довільного базису
довільного базису  . Тепер для довільної точки
. Тепер для довільної точки 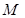 площини можна побудувати вектор
площини можна побудувати вектор  (так званий радіус-вектор точки
(так званий радіус-вектор точки 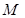 ), який розкладається за базисними векторами. Нехай
), який розкладається за базисними векторами. Нехай  .
.
Трійку елементів  називають загальною афінною системою координат. Точку
називають загальною афінною системою координат. Точку 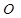 називають початком координат.
називають початком координат.

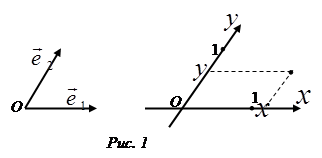 Прямі, які проходять через початок координат паралельно до векторів
Прямі, які проходять через початок координат паралельно до векторів  та
та 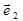 , називають координатними осями – осями а бсцис та ординат відповідно. На даних осях (їх часто позначають
, називають координатними осями – осями а бсцис та ординат відповідно. На даних осях (їх часто позначають 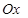 та
та  ) за допомогою стрілки вказують додатній напрям, який відповідає напрямку відповідного базисного вектора, а також відмічають одиницями кінці базисних векторів. Таким чином, довжини базисних векторів стають одиницями вимірювання на кожній із осей (рис.1). Після таких позначень базисні вектори на системі координат не зображають.
) за допомогою стрілки вказують додатній напрям, який відповідає напрямку відповідного базисного вектора, а також відмічають одиницями кінці базисних векторів. Таким чином, довжини базисних векторів стають одиницями вимірювання на кожній із осей (рис.1). Після таких позначень базисні вектори на системі координат не зображають.
Числа 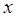 та
та 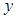 у розкладі вектора
у розкладі вектора  називають координатами точки
називають координатами точки 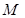 (відповідно абсцисою та ординатою) і записують
(відповідно абсцисою та ординатою) і записують  .
.
Розклад  єдиний, оскільки координати вектора відносно зафіксованого базису визначаються однозначно. Тому координати кожної точки відносно вибраної системи координат теж визначаються єдиним способом.
єдиний, оскільки координати вектора відносно зафіксованого базису визначаються однозначно. Тому координати кожної точки відносно вибраної системи координат теж визначаються єдиним способом.
Аналогічно, як і у випадку площини, вводиться поняття загальної афінної системи координат в тримірному просторі. Для цього довільно вибирають точку 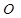 (початок координат) та через неї проводять три прямі (координатні осі), які паралельні векторам деякого базису
(початок координат) та через неї проводять три прямі (координатні осі), які паралельні векторам деякого базису  . На даних осях (їх часто позначають
. На даних осях (їх часто позначають 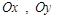 ,
, 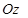 та називають осями абсцис, ординат та аплікат відповідно) стрілками вказують додатні напрямки, які відповідають напрямкам відповідних базисних векторів, а також відмічають одиницями кінці базисних векторів. Одержуємо загальну афінну систему координат
та називають осями абсцис, ординат та аплікат відповідно) стрілками вказують додатні напрямки, які відповідають напрямкам відповідних базисних векторів, а також відмічають одиницями кінці базисних векторів. Одержуємо загальну афінну систему координат 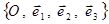 в тримірному просторі (рис.2)
в тримірному просторі (рис.2)  . Тепер для довільної точки
. Тепер для довільної точки 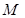 простору, побудувавши її радіус - вектор
простору, побудувавши її радіус - вектор  та розклавши його за базисними векторами, дістаємо
та розклавши його за базисними векторами, дістаємо 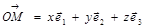 . Зауважимо, що даний розклад єдиний.
. Зауважимо, що даний розклад єдиний.
|
|
|
Числа 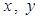 та
та 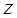 називають координатами точки
називають координатами точки 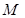 (абсцисою, ординатою та аплікатою відповідно) та записують
(абсцисою, ординатою та аплікатою відповідно) та записують 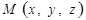 .
.
2. Якщо базис ортонормований, то систему координат, яка визначається точкою (початком координат) та базисом 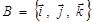 називають прямокутною декартовою системою координат у просторі. Нехай у такій системі задані дві точки
називають прямокутною декартовою системою координат у просторі. Нехай у такій системі задані дві точки 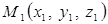 та
та  . Знайдемо співвідношення, яке виражає відстань між цими точками. Оскільки координати точок співпадають з координатами їхніх радіус-векторів, то
. Знайдемо співвідношення, яке виражає відстань між цими точками. Оскільки координати точок співпадають з координатами їхніх радіус-векторів, то  ,
, 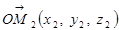 , тому
, тому 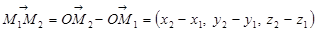 . Знайшовши довжину вектора
. Знайшовши довжину вектора  , яка дорівнює довжині відрізка
, яка дорівнює довжині відрізка  , дістаємо формулу відстані між двома точками:
, дістаємо формулу відстані між двома точками:
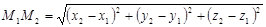 .
.
У випадку площини, коли система координат визначається точкою (початком координат) та базисом 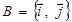 , її називають прямокутною декартовою системою координат на площині. Оскільки в цьому випадку точки та вектори визначаються двома координатами:
, її називають прямокутною декартовою системою координат на площині. Оскільки в цьому випадку точки та вектори визначаються двома координатами:  ,
, 
 , то формула відстані між двома точками набуває виду
, то формула відстані між двома точками набуває виду
 .
.
3. Нехай на прямій  вибрана точка
вибрана точка 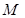 , яка ділить відрізок
, яка ділить відрізок  у деякому відомому відношенні
у деякому відомому відношенні 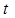 . Розглянемо задачу, як, знаючи координати заданих точок та число
. Розглянемо задачу, як, знаючи координати заданих точок та число 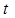 , обчислити координати точки
, обчислити координати точки 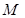 .
.
Означення. Говорять, що точка 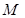 ділить відрізок
ділить відрізок  у відношенні
у відношенні 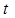 , якщо виконується рівність
, якщо виконується рівність
 . (1)
. (1)
 Відмітимо, що точка
Відмітимо, що точка 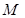 не обов’язково повинна належати відрізку
не обов’язково повинна належати відрізку  , а може лежати на прямій
, а може лежати на прямій  і поза ним. Очевидно, що якщо точка
і поза ним. Очевидно, що якщо точка 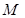 лежить всередині відрізка
лежить всередині відрізка  , то
, то  і число
і число 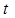 >0. Якщо точка
>0. Якщо точка 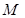 лежить поза відрізком
лежить поза відрізком  , то
, то 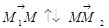 , тому
, тому 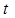 <0. Оскільки
<0. Оскільки 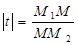 , то при
, то при 
 і точка
і точка 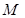 лежить на прямій
лежить на прямій  поза точкою
поза точкою 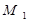 . При
. При 
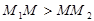 , тому точка
, тому точка 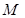 лежить на прямій
лежить на прямій  поза точкою
поза точкою 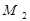 . При
. При  точка
точка 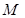 є серединою відрізка
є серединою відрізка  . При
. При 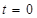 точки
точки 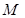 та
та 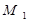 співпадають. Випадок
співпадають. Випадок 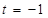 неможливий, оскільки тоді з рівності (1) випливає, що кінці відрізка співпадають.
неможливий, оскільки тоді з рівності (1) випливає, що кінці відрізка співпадають.
|
|
|
Нехай задані точки 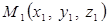 та
та  а також відношення
а також відношення 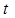 , в якому точка
, в якому точка 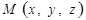 ділить відрізок
ділить відрізок  . Вважатимемо, що точка
. Вважатимемо, що точка 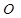 є початком координат (рис. 3). Тоді вектори
є початком координат (рис. 3). Тоді вектори  ,
, 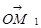 та
та  мають такі ж координати, як точки
мають такі ж координати, як точки  , тому, скориставшись рівністю (1), дістаємо
, тому, скориставшись рівністю (1), дістаємо  , звідки
, звідки
 .
.
Прирівнюючи відповідні координати векторів в обох частинах одержаної рівності, дістаємо 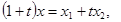
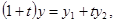
 . Остаточно,
. Остаточно,
 ,
,  ,
, 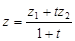 . (2)
. (2)
Одержані співвідношення називають формулами поділу відрізка у даному відношенні. Нагадаємо, що при  точка
точка 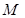 є серединою відрізка
є серединою відрізка  . Тому рівності
. Тому рівності
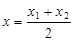 ,
, 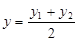 ,
, 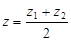 .
.
задають координати середини відрізка  . Зауважимо, що рівності (2) стосуються довільної афінної системи координат, а також, що у двомірному випадку (тобто у випадку, коли точки та вектори задаються двома координатами) в одержаних рівностях просто не розглядають вирази, які містять змінну
. Зауважимо, що рівності (2) стосуються довільної афінної системи координат, а також, що у двомірному випадку (тобто у випадку, коли точки та вектори задаються двома координатами) в одержаних рівностях просто не розглядають вирази, які містять змінну 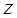 .
.
Знайдемо координати точки перетину медіан трикутника, вершини якого знаходяться в точках  . Нехай
. Нехай 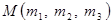
 – середина відрізка
– середина відрізка 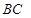 ,
,  - шукана точка. Оскільки
- шукана точка. Оскільки 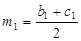 ,
, 
 , то, скориставшись рівностями (2) при
, то, скориставшись рівностями (2) при  (у такому відношенні, рахуючи від вершини трикутника, ділить медіани точка їх перетину), дістаємо
(у такому відношенні, рахуючи від вершини трикутника, ділить медіани точка їх перетину), дістаємо
 ,
, 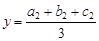 ,
,  ,
,
тобто координати центра маси трикутника рівні середнім арифметичним відповідних координат вершин трикутника.
4. Розглянемо довільний трикутник 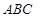 та візьмемо на його сторонах
та візьмемо на його сторонах  та
та 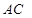 точки
точки  відповідно. Нехай
відповідно. Нехай  . Вірне наступне твердження.
. Вірне наступне твердження.
Теорема (теорема Чеви). Відрізки 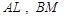 та
та  перетинаються в одній точці тоді і тільки тоді, коли виконується рівність
перетинаються в одній точці тоді і тільки тоді, коли виконується рівність  .
.
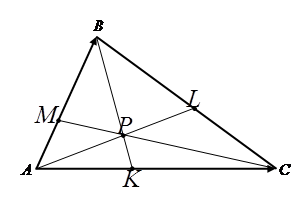
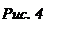 Доведення. Введемо в розгляд афінну систему координат, вибравши за початок координат точку А та базис
Доведення. Введемо в розгляд афінну систему координат, вибравши за початок координат точку А та базис  (рис. 4). У цій системі точки матимуть наступні координати:
(рис. 4). У цій системі точки матимуть наступні координати: 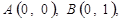

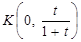 ,
, ,
, 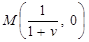 . Нехай відрізки
. Нехай відрізки 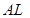 та
та 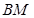 перетинаються у точці
перетинаються у точці 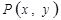 . Тоді із колінеарності векторів
. Тоді із колінеарності векторів 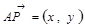 та
та  , а також векторів
, а також векторів  та
та 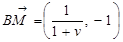 дістаємо систему
дістаємо систему 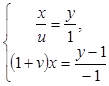 , звідки
, звідки 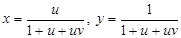 . Якщо відрізок
. Якщо відрізок  проходить через точку
проходить через точку 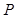 , то із колінеарності векторів
, то із колінеарності векторів  та
та 
 , дістаємо
, дістаємо  , звідки
, звідки  .
.
Із одержаних співвідношень також випливає те, що якщо  , то вектори
, то вектори  та
та 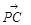 колінеарні, тобто, що відрізок
колінеарні, тобто, що відрізок  проходить через точку
проходить через точку 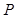 перетину двох інших відрізків.
перетину двох інших відрізків.
Теорема доведена.
5. Наведемо приклади розв’язання деяких задач.
Задача 1. Задано прямокутник  . Довести, що для довільної точки
. Довести, що для довільної точки 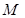 виконується рівність
виконується рівність  .
.
Доведення. Введемо прямокутну систему координат наступним чином: точку 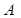 виберемо початком координат, пряму
виберемо початком координат, пряму 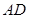 - віссю
- віссю 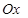 , а пряму
, а пряму 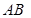 - віссю
- віссю  . Нехай
. Нехай  . Тепер кожна точка матиме свої координати:
. Тепер кожна точка матиме свої координати: 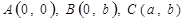 ,
, . Скориставшись формулою відстані між двома точками, дістаємо
. Скориставшись формулою відстані між двома точками, дістаємо
|
|
|
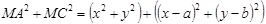 ,
, 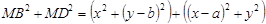 ,
,
що і доводить потрібну рівність.
Задача 2. У трикутній піраміді 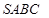 вершини сполучено з центрами протилежних граней. Довести, що утворені відрізки перетинаються в одній точці та діляться нею у відношенні 3:1, рахуючи від вершини.
вершини сполучено з центрами протилежних граней. Довести, що утворені відрізки перетинаються в одній точці та діляться нею у відношенні 3:1, рахуючи від вершини.
Розв’язання. По-перше, зауважимо, що дану задачу ми уже розглядали в лекції 2 та розв’язали її векторним методом. Зараз ми скористаємось координатним методом. Введемо в розгляд загальну афінну систему координат, вибравши точку 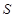 початком координат та взявши базис
початком координат та взявши базис  . Тоді вершини піраміди матимуть наступні координати:
. Тоді вершини піраміди матимуть наступні координати: 
 . Нехай точки
. Нехай точки 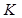 та
та 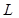 - точки перетину медіан трикутників
- точки перетину медіан трикутників 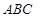 та
та 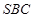 відповідно. Використавши результати пункту 4, знаходимо координати точок
відповідно. Використавши результати пункту 4, знаходимо координати точок 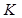 та
та 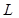 :
: 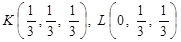 . Нехай точки
. Нехай точки 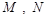 ділять відрізки
ділять відрізки 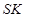 та
та 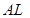 у відношенні 3:1, рахуючи від точок
у відношенні 3:1, рахуючи від точок 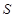 та
та 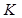 відповідно. Скориставшись формулами поділу відрізка у даному відношенні при
відповідно. Скориставшись формулами поділу відрізка у даному відношенні при  , дістаємо
, дістаємо  ,
,  . Оскільки точки
. Оскільки точки 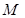 та
та 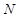 співпадають, то твердження доведено.
співпадають, то твердження доведено.
Лекції 4, 5
Скалярний, векторний та мішаний добутки векторів. Їх властивості та застосування.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 640; Нарушение авторских прав?; Мы поможем в написании вашей работы!