Различные случаи решения систем линейных уравнений

Классификация систем линейных уравнений.

1⁰. Система уравнений называется совместной, если она имеет, хотя бы одно решение;

2⁰. Система уравнений называется совместной и определенной, если она имеет только одно решение;

3⁰. Система уравнений называется совместной и неопределенной, если она имеет множество решений;

4⁰. Система уравнений называется несовместной, если она не имеет решений;

5⁰. Система уравнений называется квадратной, если число неизвестных 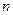равно числу уравнений , . Количество неизвестных такой системы называется порядком системы.

В дальнейшем мы будем рассматривать системы только второго и третьего порядков.

1⁰. Рассмотрим систему уравнений:

(1.3)

Решением системы (1.3) является пара чисел:

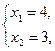или (4;3).

Покажем это. Подставим значения неизвестных в систему (1.3), получим:

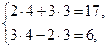
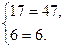
При подстановке в уравнения значений неизвестных мы получили верные равенства. Потому пара чисел (4;3) является решением системы. Других решений система не имеет, следовательно, система уравнений (1.3) является совместной и определенной.

Геометрическое изображение этого случая решения приведено на рис. 1.1. Прямые и , изображающие уравнения системы, пересекаются в точке .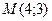

Рис. 1.1

2⁰. Рассмотрим систему уравнений:

(1.4)

Второе уравнение системы (1.4) может быть получено из первого путем умножения всех его членов на 3, аналогично первое уравнение можно получить из второго путем деления всех его членов на 3. Поэтому вместо системы мы имеем фактически одно уравнение, и система эквивалентна одному из этих уравнений. Уравнение, как известно, имеет, бесконечное множество решений имеет, а значит и система. Решениями системы (1.4) являются, например, такие пары чисел: (0;4), (3;0), (6;–4). Следовательно, система (1.4) является совместной и неопределенной системой уравнений.

Геометрически этот случай иллюстрирует рис. 1.2. Прямые и , изображающие уравнения системы (1.4), сливаются в одну прямую. И координаты любой точки этой прямой являются решением системы уравнений (1.4)

Рис. 1.2

3⁰. Рассмотрим систему уравнений:

(1.5)

Уравнения имеют одинаковые левые части и неравные свободные члены. Система (1.5) не может иметь решений, так как если при некоторой паре значений в верное равенство обращается первое уравнение, наверняка при этих значениях и 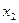не обратится в верное равенство второе и наоборот. Подставим, например, пару чисел (4;–6) в уравнения системы (1.5), получим:

Первое уравнение обратилось в верное равенство, второе уравнение – в неверное равенство, пара чисел (4;–6) не является решением данной системы. Следовательно, система уравнений (1.4) является несовместной системой.

Геометрически этот случай представлен на рис. 1.3. Прямые и , изображающие уравнения системы (1.5), параллельны и не имеют точек пересечения.

Рис. 1.3

2. Решение систем линейных уравнений
2-го и 3-го порядков методом Крамера

Габриель Крамер (1704-1752) – швейцарский ученый. Родился и получил образование в Женеве. С 1724 года преподавал математику в Женевской кальвинистской академии (с 1734года – профессор математики, с 1750 года – профессор философии). Член Совета Шестидесяти (с 1749) и член Лондонского королевского общества (академии наук) (с 1749).

Основные направления исследований – геометрия, теория вероятностей и линейная алгебра. В алгебре установил правило решения системы линейных уравнений с буквенными коэффициентами (правило Крамера), заложил основы теории определителей.

Рассмотрим теорему Крамера для системы уравнений третьего порядка. Однако, доказано, что формулы Крамера применимы для решения системы с любым количеством неизвестных.

Рассмотрим систему трех уравнений с тремя неизвестными (третьего порядка):

(2.1)

Матрицей системы является матрица:

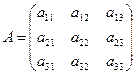(2.2)

Определение 2.1. Определитель 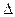, составленный из коэффициентов при неизвестных

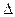
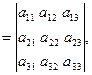(2.2)

называется определителем системы линейных уравнений (2.1). Алгоритм решения системы уравнений (2.1) сформулирован в теореме Крамера.

Теорема 2.1. Пусть 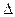– определитель (2.2) системы линейных уравнений (2.1), а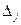 – определитель, полученный из определителя 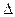заменой 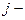го столбца столбцом свободных членов. Тогда, если 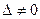, то система имеет единственное решение, определяемое по формулам:

(2.3)

где

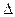
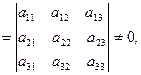
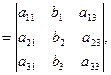
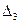
Рассмотрим примеры решения систем уравнений с тремя и двумя неизвестными методом Крамера.

Задача 2.1. Решить систему уравнений:

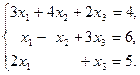(2.4)

Найдем определитель системы уравнений (2.4), разлагая его по элементам 3 строки, содержащей нуль:

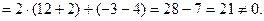
Определитель системы не равен нулю, поэтому система имеет единственное решение. Вычислим :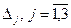

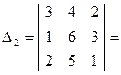
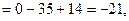
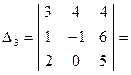
Таким образом, решением системы уравнений (2.4) является тройка чисел:

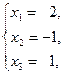или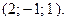

Задача 2.2. Решить систему уравнений:

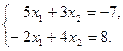(2.5)

Решение. Вычислим определитель системы (2.5):

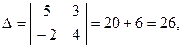
Определитель системы 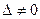, поэтому система имеет единственное решение. Найдем и :

отсюда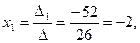

Решение системы уравнений (2.5):

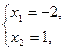или .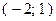

Дата добавления: 2013-12-13