Разработка стратегии снабжения строительной фирмы материальными ресурсами

Разработка стратегии снабжения строительной фирмы материальными ресурсами зависит от множества факторов и специфики внутрифирменных процессов.Определяющими при этом являются процессы создания и хранения запасов. Процессами, связанными с проблемой запасов, принято называть такие процессы, которые требуют либо обоих, либо одного из двух следующих решений:

- сколько заказывать (производить или покупать);

- когда заказывать.

Задача управления запасами возникает тогда, когда существует некоторый критерий, величина которого изменяется в зависимости от уровня запасов, снижаясь до определенного уровня и повышаясь после этого уровня. В качестве такого критерия целесообразно применять затраты на хранение материалов и издержки, вызванные их дефицитом. Так как термины «затраты» и «издержки» не полностью характеризуют этот критерий, то для обозначения затрат и ущерба от их дефицита используют термин «потери».

Потери – это полный экономический ущерб, вызванный затратами строительной организации на хранение запаса материалов, омертвлением средств в этом запасе, издержками, связанными с недостатком строительных материалов, и замедлением ввода в строй сооружаемых объектов. Потери могут быть разделены на потери от хранения и потери от дефицита. Потери от хранения разделяются на элементные затраты и потери:

- затраты на содержание складов и обслуживающего персонала;

- потери от физической порчи и убыли хранимого имущества;

- потери от морального старения конструкций и деталей;

- потери от омертвления средств в запасах материалов.

Первые три группы потерь являются затратными видами потерь и отражаются в фактической себестоимости строительства.

Потери от омертвления оборотных средств в запасах материалов действуют на экономику строительной организации двояко:

- строительная организация платит проценты за кредиты, связанные с содержанием запасов;

- чрезмерными запасами одних материаловю, связываются оборотные средства, необходимые для приобретения других. В этом случае возникнет дефицит некоторых материалов или дополнительная финансовая нагрузка на строительную организацию. Второй вид потерь косвенно отражается в себестоимости строительной продукции или сказывается на темпах строительства.

Для получения функций потерь необходимо установить количественные зависимости между потерями и средними запасами строительных материалов, пользуясь методами корреляционно-регрессионного анализа.

Для решения этих задач используются уравнения экономичного размера партии, а также аппарат линейного, динамического и квадратичного программирования.

Задача разработки стратегии снабжения может решаться с использованием методов динамического программирования.

Модели динамического программирования предусматривают нахождение оптимального решения не только в зависимости от значений переменных, но и во времени.

Динамическое программирование – метод, позволяющий найти экстремум общего критерия многошагового процесса, при этом на каждом шаге оптимизируется поведение системы на последующем этапе, учитывая ее состояние на предыдущем. Решения, принимаемые на дальнейших шагах, не оказывают влияния на предыдущие решения, но текущие управляющие решения «проявляются» как в период, относящийся непосредственно к моменту принятия решения, так и в последующие периоды.

В основу метода динамического программирования положен известный принцип, сформулированный Ричардом Беллманом: «Оптимальное управление обладает таким свойством, что каково бы ни было начальное состояние и начальное управление, последующее управление должно быть оптимальным по отношению к состоянию, получающемуся в результате действия начального управления». Если в данный момент времени не выбирается оптимальное управление, то впоследствии ошибку исправить невозможно.

Рассмотрим фирму, которая должна разработать календарный план поставок некоторого материала на плановый период. Спрос может быть стационарным (постоянным) и нестационарным. Для упрощения примем, что спрос является величиной детерминированной. Размеры поставляемых партий влияют на экономические показатели работы фирмы.

Цель задачи – разработать такой план поставок, при котором общая сумма затрат на поставку материалов и хранение запасов минимизируется при условии полного и своевременного удовлетворения потребности.

Преобразуем качественное описание задачи в математическую модель.

Построение модели. Дано: d_n – потребность в материале в n-м интервале (n=1:N). Найти: q_n– объем поставок в n-м интервале.

Введем обозначения y_n – уровень запаса на начало n-го интервала, z_n – уровень запаса на конец n-го интервала. Предположим также, что для каждого отрезка n затраты на содержание – C_n зависят от объема поставки q_n и от уровня запаса на конец отрезка z_n.

Тогда необходимо – минимизировать целевую функцию

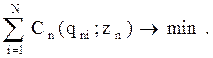, (1.2)

При этом на значения переменных накладываются следующие ограничения:

- q_n= 0,1,2,3,... (n = 1– N) – объемы поставок целочисленны;

- для руководства фирмы желательно, чтобы на конец периода запасы были равны 0: z_n = 0;

- ставится условие полного и своевременного удовлетворения потребности, следовательно необходимо соблюдать;

- балансовое соотношение z_n=y_n+q_n-d_n, z_n³0.

Вычислительный процесс строится от конечного состояния к начальному. Под состоянием системы будем понимать уровень запаса на начало периода – y_n. Управляемая переменная - объем поставок – q_n. Так как вычислительный процесс идет с конца, в системе используется обратная система индексов:

– F_n (y) –стоимость, соответствующая стратегии минимальных затрат на n оставшихся отрезках при начальном уровне запасов y;

– Q_n (y) –поставка, обеспечивающая состояние Fn (y).

Для n=0, так как уровень запасов на конец планового периода равен 0, можно записать F₀(0)=0.

Для n=1, начальный уровень запасов y₁ не может быть больше, чем d₁, т.к. z₁=0. Для полного удовлетворения потребности q должен быть равен d₁–y₁=q₁. F₁(y)=C₁(q₁,z₁) +0.

Для n=2, F₂(y)=C₂ (q₂, y₂+q₂–d₂) + F₁(y₂+q₂–d₂), т.к. z₂= y₂+q₂–d₂ и y₂+q₂–d₂=z₂=y₁.

Величина y₂ не может превышать d₁+d₂, т.к. z₀=0.

На переменную q₂ при заданном y₂ накладываются следующие ограничения:

q₂ ³ d₂ – y₂, т.к. необходимо полное удовлетворение потребности на отрезке n;

q₂ £ d₁ + d₂ – y₂, т.к. конечный запас равен 0.

Выполненный анализ ситуации для n=2 можно выразить следующим общим выражением: d₂–y₂ £ q₂ £ d₁+d₂ –y₂.

Принцип динамического программирования реализуется в рекуррентном соотношении Беллмана: 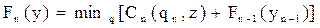, причем для отыскания минимума перебираются все неотрицательные значения q, заключенные в пределах d_n – y_n £ q_n £ d₁+d₂+...+d_n –y_n.

Принимаемые решения об объеме поставок в 1-м интервале влияют на уровень запасов на начало 2-го интервала. Если первая величина известна, то во 2-м интервале можно действовать оптимальным образом. Однако поставки в первом интервале были оптимизированы на предыдущем шаге.

При определении оптимального объема поставок во 2-м интервале необходимо рассматривать сумму затрат во 2-м интервале и сумму оптимальных затрат 1-го интервала.

В рекуррентном соотношении последовательность операций является обратной действительной их последовательности во времени.

Задача 1.4. Используя метод динамического программирования, определить стратегию снабжения строительной фирмы одним из видов строительных материалов на 4 календарных месяца, которая обеспечивает минимальные затраты на доставку и хранение материала при условии полного удовлетворения потребности, основываясь на следующей информации.

Затраты на заказ партии – 13 у.д.е. за партию. Затраты на хранение 1 ед. материала на складе – 1 у.д.е. Стоимость 1 ед. материала – 2 у.д.е. Спрос на материал по интервалам стационарен и составляет 3 ед. Ограничения по складским площадям составляют 4 ед. хранимого материала. Ограничения на объем поставки – 5 ед. материала.

Для руководства фирмы желательно, чтобы запасы материала в конце планового периода были равны 0.

Решение 1.4. Приведем формализованную постановку задачи. d_n=3, функция затрат состоит из двух составляющих:

- затрат на поставку материалов, состоящих из двух частей: условно постоянной – заказ партии 13 у.д.е. и условно переменной 2 у.д.е./ ед. заказа;

- затраты на содержание запаса, которая является линейной функцией объема запаса – 1 у.д.е./ хранимую ед.

Стоимость доставки материала, зависящая от размера партии и затрат на хранение материала (табл. 7), определяется по формуле

C_n (q_n,z_n) = C(q_n) + h•Z_n. (3)

Таблица 7

Стоимость доставки материала в зависимости от размера партии

n
C(n)
h=1

Складские площади ограничены Þ Z_n Î [ 0, 4 ].

Объем поставок также ограничен Þ Q_n Î [ 0, 5].

Отсюда получаем следующие ограничения:

(3 – y_n) £ q_n £ min (5, 7 – y_n),

где 5 – ограничение на объем поставки; (7–y_n) – ограничение по складским помещениям; (3-y_n) – условие полного обеспечения потребности.

При наличии приведенных выше данных можно составить динамическое рекуррентное соотношение, отражающее специфику задачи.

На каждом шаге строится таблица, в которой предусмотрено по 1 строке для каждого начального уровня запаса и по одному столбцу для каждого возможного значения поставки. Некоторые клетки должны быть заштрихованы (запрещены) согласно ограничениям.

Для каждого фиксированного y значение функции f_n(y) представляет собой минимальную из всех сумм в клетках данной строки, а q_n (y) – соответствующий объем поставки. Любое другое значение q обеспечивает более высокие затраты.

Рассмотрим первый шаг – n=1: F₁(y_n) = C(q_n,z_n) = С(3-y_n) (табл. 8).

Таблица 8

Возможные объемы поставки для 1-го планового периода

q1   y1							Q опт	Сq(y)
				19+0
			17+0
		15+0
							-	-

Прокомментируем результаты, полученные на первом шаге. Если в начале первого периода фирма имеет на складе 1 единицу материала, то для полного удовлетворения потребности поставка должна быть равна 3 ед. материала, а соответствующие ей денежные затраты – 19 у.д.е.

В то же время, при наличии на складе 2 ед. необходимого материала поставка должна составить 1 ед., а затраты – 15 у.д.е. Любые другие значения поставки не соответствуют условиям задачи.

Для нахождения оптимальных объемов поставок во втором плановом периоде будем использовать таблицу с результатами оптимальных объемов поставки первого планового периода (табл. 9).

Таблица 9

Возможные объемы поставки для 2-го планового периода

q2   y2							Qопт	Сq(y)
				19+ 0+	21+ 1+	23+ 2+
			17+ 0+	19+ 1+	21+ 2+	23+ 3+
		15+ 0+	17+ 1+	19+ 2+	21+ 3+
	0+ 0+	15+ 1+	17+ 2+	19+ 3+
	0+ 1+	15+ 1+	19+ 3+

Необходимо отметить, что верхние клетки таблицы запрещены, так как в них не выполняется условие полного удовлетворения потребности, а нижние клетки запрещены, так как в них не соблюдается условие о нулевом конечном уровне запаса.

Для нахождения оптимальных объемов поставок в третьем плановом периоде будем использовать таблицу с результатами оптимальных объемов поставки второго планового периода (табл.10).

Таблица 10

Возможные объемы поставки для 3 планового периода

q3   y3							Qопт	Сq(y)
				19+ 0+	21+ 1+	23+ 2+
			17+ 0+	19+ 1+	21+ 2+	23+ 3+
		15+ 0+	17+ 1+	19+ 2+	21+ 3+	23+ 4+
	0+ 0+	15+ 1+	17+ 2+	19+ 3+	21+ 4+
	0+ 1+	15+ 2+	17+ 3+	19+ 4+

При определении оптимальных объемов поставки в третьем интервале нижние клетки таблицы оказались заштрихованными, так как при их использовании в расчетах нарушается ограничение на максимальный размер склада.

Для нахождения оптимальных объемов поставок в четвертом плановом периоде будем использовать таблицу с результатами оптимальных объемов поставки третьего планового периода (табл.11).

Как показывают результаты расчетов, оптимальной является стратегия снабжения, обеспечивающая минимальные затраты на поставку и хранение материалов, равные 46 у.д.е. Из них 4 у.д.е. тратятся на хранение материала, а 42 у.д.е. на доставку.

Для того чтобы составить план снабжения, необходимо расшифровать обратную систему индексов. Тогда объем поставки для 1-го планового периода необходимо взять из табл. 11, объем поставки для 4-го периода – из табл. 8. В результате получим следующий план снабжения организации строительным материалом (табл.12).

Таблица 11

Возможные объемы поставки для 4 планового периода

q4   y4							Qопт	Сq(y)
				19+ 0+	21+ 1+	23+ 2+	3,4
			17+ 0+	19+ 1+	21+ 2+	23+ 3+
		15+ 0+	17+ 1+	19+ 2+	21+ 3+	23+ 4+
	0+ 0+	15+ 1+	17+ 2+	19+ 3+	21+ 4+
	0+ 1+	15+ 2+	17+ 3+	19+ 4+

Таблица 12

Оптимальный план поставок

	1-й период	2-й период	3-й период	4-й период
Yn
Qn
Zn

Таким образом, в первом периоде необходимо поставить 0 ед. материала, во втором – 5 ед., в третьем – 0 ед., а в четвертом – 3 ед. Для выполнения этого плана в начале планового периода фирма должна иметь на складе 4 ед. запаса материала. Правильность расчетов подтверждается выполнением балансового соотношения: 4+8 = 12+0.

Любая другая стратегия сопровождается более высокими денежными затратами. В то же время по последней расчетной таблице можно находить оптимальную карту для снабжения в соответствии с любым из возможных начальных уровней запаса.

Дата добавления: 2013-12-13