Упражнения. 1. Найти угол наклона к оси ох касательной, проведенной к параболе в точке

1. Найти угол наклона к оси ох касательной, проведенной к параболе 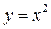в точке .

Ответ: .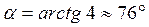

2. Найти на параболе 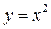такую точку , чтобы касательная к параболе, проведенная в этой точке, составила с осью ох угол .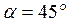

Ответ: .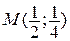

3. В момент времени найти скорость v и ускорение a точки, движущейся по оси ох по закону .

Ответ: ; .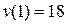

4. Количество y произведенной за время t продукции описывается функцией . Найти производительность труда предприятия.

Ответ: 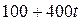(ед. продукции за ед. времени).

5. Функция определяет зависимость себестоимости продукции y (в рублях) от объема x выпускаемой продукции (в некоторых единицах). Найти предельную себестоимость продукции.

Ответ: 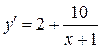(руб/ед.).

6. Кривая спроса 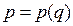имеет уравнение 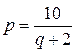. Найти предельный (маржинальный) доход от реализации продукции.

Ответ: (ден. ед./ед. товара).

7. Найти производную функций:

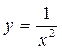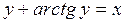а) ; б) ; в) ; г) ; д)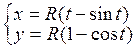

Ответ: а) ; б) ; в) ;

г) ; д) .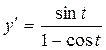

Производная обратной функции.

Пусть дана возрастающая или убывающая функция, определенная на некотором отрезке 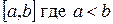. Пусть f(a)=c, f(b)=d. Для определенности будем далее рассматривать возрастающую функцию.

Рассмотрим два различных значения x₁ и x₂, принадлежащих отрезку 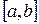. Из определения возрастающей функции следует, что если x₁ < x₂ и 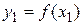, , то y₁<y₂. Следовательно, двум различным значениям x₁ и x₂ соответствуют два различных значения функции y₁ и y₂. Справедливо и обратное, т.е. y₁ < y₂. 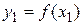, а , то из определения возрастающей функции следует, что x₁ < x₂. Таким образом, между значениями x и соответствующими значениями y устанавливается взаимно однозначное соответствие.

Рассматривая эти значения y как значения аргумента, а значения x как значения функции, получаем x как функцию y: .

Эта функция называется обратной для функции . Очевидно, что 1) функция является обратной для функции ;

2) если возрастающая (или убывающая) функция непрерывна на отрезке 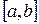, причем f(a)=c, f(b)=d, то обратная функция определена и непрерывна на отрезке .

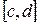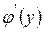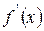Теорема 1. Если для функции существует обратная функция , которая в рассматриваемой точке y имеет производную , отличную от нуля, то в соответствующей точке x функция имеет производную, равную 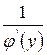, т.е. справедлива формула .

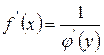Другими словами, производная одной из двух взаимно обратных функций равна единице, деленной на производную второй из этих функций при соответствующих значениях x и y.

Доказательство. Возьмем приращение , тогда 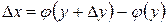. Поскольку - монотонная функция, то 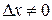, а значит имеет место тождество 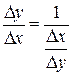. (5)

Так как функция - непрерывная, то 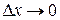при . Переходя к пределу при в обеих частях равенства (5), получим

или ,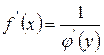

Что и требовалось получить.

Используя доказанную теорему, получим табличные производные функций y=arcsinx и y=arctgx.

Пример 7. Найти производную функции y=arcsinx.

Решение. Рассмотрим обратную функцию x=siny. Найдем . На основании (5) имеем, т.е. . Перед корнем берется знак плюс, так как функция y=arcsinx принимает значения на отрезке и, следовательно .

Пример 8. Найти производную функции y=arctgx.

Решение. Рассмотрим обратную функцию x=tgy. Найдем . На основании (5) имеем 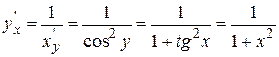, т.е. .

Логарифмическое дифференцирование или производная сложной показательной функции.

Сложной показательной функцией – называется функция у которой и основание и показатель степени являются функциями от х, например, , вообще всякая функция вида есть сложная показательная функция.

Теорема 1. Если , то .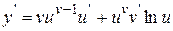

Доказательство. Логарифмируем функцию y: . Дифференцируя полученное равенство по х, будем иметь: , откуда . Подставляя сюда выражение , получаем .

Таким образом, производная сложной показательной функции состоит из двух слагаемых: первое слагаемое получается, если при дифференцировании предположить, что и есть функция от х, а v есть постоянная (т.е. если рассматривать 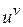как степенную функцию); второе слагаемое получается, если предположить, что v есть функция от х, а u=const (т.е. если рассматривать 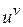как показательную функцию).

Пример 9. Найти производную функции y=x^х.

Решение. Логарифмируем функцию y: 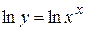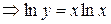. Дифференцируем полученное равенство по х: . Таким образом, . Учитывая условие задачи, получаем .

Пример 10. Найти производную функции y= .

Решение. Логарифмируем функцию y: 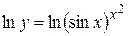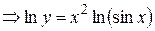. Дифференцируем полученное равенство по х: . Таким образом, . Учитывая условие задачи, получаем .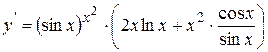

Дата добавления: 2013-12-13