Нахождение наибольшего и наименьшего значений функции, непрерывной на отрезке

Схема исследования функции на возрастание-убывание и точки экстремума.

1. Находим область определения функции. То есть находим все те значения x, для которых существует (можно найти) значение функции . Заодно устанавливаем интервалы непрерывности и точки разрыва функции.

2. Находим производную .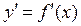

3. Находим точки (значения x), подозрительные на экстремум (критические точки). То есть находим те точки (значения x), в которых производная функции или равна нулю, или не существует:

а)

б) 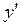не существует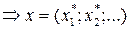

4. Наносим все найденные в пунктах (а) и (б) подозрительные на экстремум точки на область определения функции (на ось ох) и фиксируем (например, дугами) интервалы, на которые разобьется область определения этими точками. Так как внутри каждого такого интервала производная функции существует и не обращается в нуль, то в каждом интервале производная сохраняет свой знак, который может измениться лишь при переходе к другому интервалу. С помощью вычисления производной в пробных внутренних точках определяем знак производной в каждом интервале. По найденным знакам производной устанавливаем интервалы возрастания и убывания функции, а по смене знака производной определяем точки экстремума функции (точки максимума и минимума).

5. В найденных точках максимума и минимума вычисляем значения функции и тем самым определяем вершины и впадины графика функции, отмечая заодно, округлые они или острые.

Пример 2. Исследовать функцию 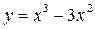на возрастание-убывание и точки экстремума.

Решение. Действуем по изложенной выше схеме.

1. Функция 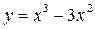определена (а следовательно, и непрерывна) для любых x, то есть на всей числовой оси ох (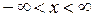). Значит, её график – сплошная (без разрывов) линия.

2. Найдем производную :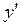

.

3. Найдем точки (значения x), подозрительные на экстремум:

а) .

б) 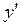не существует Þ таких x нет.

4. Нанесем найденные подозрительные на экстремум точки и на область определения функции (на ось ох). Ось ох этими точками разобьется на три интервала:

Определяем знаки производной 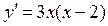в этих интервалах (они отмечены на рис. выше). Тем самым устанавливаем интервалы возрастания функции 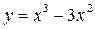(они помечены стрелкой вверх) и интервал ее убывания (стрелка вниз), а также устанавливаем, что точка – точка максимума функции, а точка – точка ее минимума.

5. Находим (вычисляем) значения функции 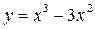в точках ее максимума и минимума, устанавливая тем самым вершины и впадины графика функции:

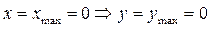; точка 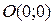– вершина графика функции (округлая, т.к. ).

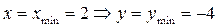; точка 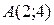– впадина графика функции (округлая, т.к. ).

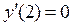6. В дополнение к проведенному исследованию найдем еще точки пересечения графика функции с осями координат:

а) С осью ох:

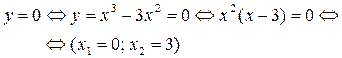
б) С осью оу:

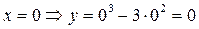
А теперь построим этот график (рис. 4):

Пусть – функция, непрерывная на некотором отрезке 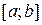оси ох (рис. 5)

Ставится задача: указать схему нахождения тех точек отрезка 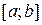оси ох, в которых функция достигает своего наибольшего значения и своего наименьшего значения , и найти эти и.

Сразу отметим, что такие точки на отрезке 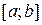заведомо существуют (это доказано). А вот на интервале 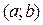их может и не быть. То есть на интервале функция своих наибольшего и наименьшего значений может и не иметь. Например, функция 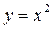на отрезке 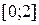свое наименьшее значение достигает в точке 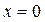, а свое наибольшее значение достигает в точке . А вот на интервале своих наибольшего и наименьшего значений функция 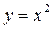, очевидно, не имеет (не достигает).

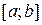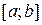Вернемся к рис. 5, на котором изображена произвольная непрерывная на отрезке функция . Здесь достигается функцией на конце a отрезка , а – в точке x₁, являющейся одной из точек минимума функции. И вообще, очевидно, что и при любой другой форме графика непрерывной функции наибольшее и наименьшее значения достигаются ею на отрезке 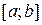или в её точках экстремума, содержащихся на этом отрезке, или на концах отрезка. Отсюда вытекает следующая

схема нахождения и функции на отрезке :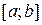

1. Находим производную .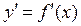

2. Находим принадлежащие отрезку 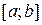точки, подозрительные на экстремум.

3. Не исследуя этих точек, вычисляем значение функции во всех найденных подозрительных точках, а также на концах a и b отрезка 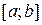. Из всех найденных значений y выбираем и. А заодно и устанавливаем, в каких точках отрезка 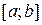эти идостигаются.

Пример 3. На отрезке 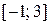найти наибольшее и наименьшее значения функции .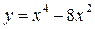

Решение. Реализуем изложенную выше схему.

1. Найдем :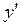

.

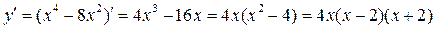2. Найдем на отрезке 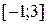точки (значения x), подозрительные на экстремум:

а) .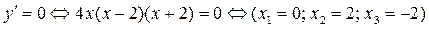

б) 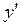не существует Þ таких x нет.

На отрезке 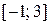содержатся лишь две подозрительные на экстремум точки: это и .

3. Вычисляем значении функции 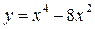в обеих найденных подозрительных точках, а также на концах отрезка, и выберем из найденных значений функции наибольшее и наименьшее:

; ; ;

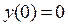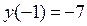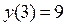
Ответ: ; .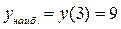

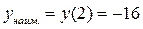Дата добавления: 2013-12-13