Понятие интегральной суммы и определённого интеграла.

Задача о площади криволинейной трапеции.

Определенный интеграл

Методы интегрирования

1. Первый — используя свойства интеграла и таблицу.

2. Второй — метод разложения, суть которого в преобразовании подинтегральной функции.

3. Третий — замена переменной.

Если функция f (x) непрерывна, а функция j (t) имеет непрерывную производную j¢ (t), то имеет место формула

ò f (j (t)) j¢ (t) dt = ò f(x) dx, где x = j (t).

Можно привести примеры вычисления интеграла с помощью перехода от левой части к правой в этой формуле, а можно привести примеры обратного перехода.

Примеры.

3.1. I = ò cos(t ³) t ² dt. Пусть t ³ = x, тогда dx = 3 t ² dt или t ² dt = dx/ 3.

.

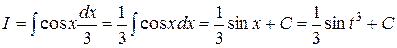3.2. 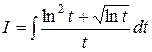. Пусть ln t = x, тогда dx = dt/t.

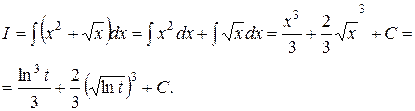
3.3. . Пусть x = cos t, тогда dx = - sin t dt, и

.

3.4. . Пусть x = sin t, тогда dx = cos dt, и

.

Пусть на промежутке [ a; b ] задана неотрицательная функция f (x). Требуется найти площадь S криволинейной трапеции, ограниченной кривой y = f (x), прямыми x = a, x = b, y = 0.

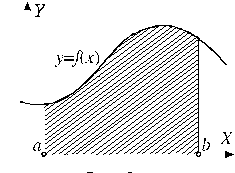
Наметим общий подход: разобьем весь отрезок на несколько равных отрезков; построим ломаную прямую; вычислим площадь получившегося многоугольника, и, если ломаная прямая достаточно близка к кривой y = f (x), то площадь многоугольника приблизительно равна площади криволинейной трапеции.

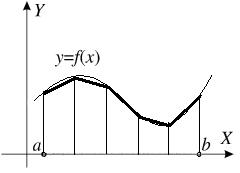
Пусть на промежутке [ a; b ] задана функция f (x). Будем считать функцию непрерывной, хотя это не обязательно. Выберем на промежутке [ a; b ] произвольные числа x ₁, x ₂, x ₃, ¼, x_{n -1}, удовлетворяющие условию:
a < x ₁,< x ₂<¼< x_{n -1},< b. Эти числа разбивают промежуток [ a; b ] на n более мелких промежутков: [ a; x ₁], [ x ₁; x ₂], ¼, [ x_{n -1}; b ]. На каждом из этих промежутков выберем произвольно по одной точке: c ₁Î[ a; x ₁], c ₂Î[ x ₁; x ₂], ¼, c_n Î[ x_{n -1}; b ].

Введем обозначения:D x ₁ = x ₁ – a; D x ₂ = x ₂ – x ₁; ¼, D x_n = b – x_{n- 1}.

Составим сумму: .

Она называется интегральной суммой функции f (x) по промежутку [ a; b ]. Очевидно, что интегральная сумма зависит от способа разбиения промежутка и от выбора точек c_i.

Каждое слагаемое интегральной суммы представляет собой площадь прямоугольника, покрытого штриховкой (Рис. 1).

Рассмотрим процесс, при котором 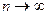, т.е. число точек разбиения неограниченно возрастает. Определенным интегралом 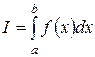от функции по промежутку [ a; b ] называется предел, к которому стремится интегральная сумма, если этот предел существует:

.

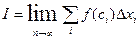Если такой предел существует, то он не зависит от первоначального разбиения промежутка [ a; b ] и выбора точек c_i.

Число a называется нижним пределом интегрирования, ачислоb ¾ верхним пределом интегрирования.

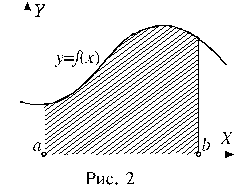
Рассмотрим криволинейную трапецию. На Рис. 2 криволинейная трапеция выделена штриховкой. Площадь S этой трапеции определяется формулой .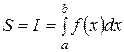

Если f (x) < 0 во всех точках промежутка [ a; b ] и непрерывна на этом промежутке (например, как изображено на рисунке 3), то площадь криволинейной трапеции, ограниченной отрезком [ a; b ] горизонтальной оси координат, прямыми x = a; x = b и графиком функции y = f (x), определяется формулой

.

Перечислим свойства определенного интеграла:

1) (здесь k ‑ произвольное число);

2) ;

3) ;

4) Если cÎ [ a; b ], то .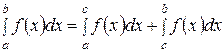

Из этих свойств следует, например, что .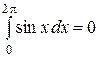

Все приведенные выше свойства непосредственно следуют из определения определенного интеграла.

Дата добавления: 2013-12-13