Моменты инерции плоских сечений

Р е ш е н и е

Задача для самостоятельного решения.

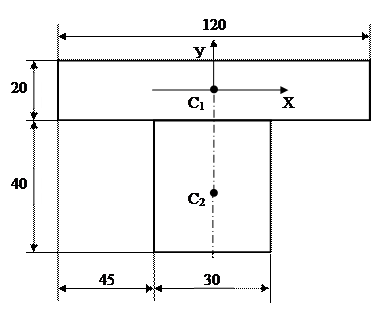Найти координаты центра тяжести сечения: х_c -? у_c -?

Размеры даны в мм, но считать удобнее в см, а потом ответ перевести в мм. Оси задать произвольно.

При рациональном выборе нача-ла координатных осей вычисления существенно упрощаются.

координатные оси Х и У проводятся через центр тяжести (С₁) первого (верхнего) прямоугольника.

1. Площади прямоугольников:

A₁ = 12·2 = 24 см²

A₂ = 4·3 = 12 см²

2. Координаты центра тяжести прямоугольников:

х₁ = 0 х₂ = 0

у₁ = 0 у₂ = -1-2 = -3 см

1. Статистические моменты прямоугольников:

S_1x = y₁·A₁ = 0·A₁ = 0 S_2x = y₂·A₂ = -3·12 = -36 см³

S_1у = x₁·A₁ = 0·A₁ = 0 S_2y = x₂·A₂ = 0·A₂ = 0

1. Координаты центра тяжести составного сечения:

При расчетах на прочность, жесткость и устойчивость используются осевые и полярные моменты инерции.

Осевым моментом инерции относительно некоторой оси называют взятую по всей площади сечения А сумму произведений площадей элементарных площадок dA на квадраты их расстояний до этой оси:

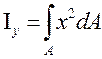
Полярным моментом инерции относительно некоторой точки (полюса О) называют взятую по всей площади сечения А сумму произведений площадей элементарных площадок dA на квадраты их расстояний до этой точки

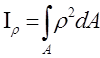
Связь между осевыми и полярным моментами инерции:

Согласно рис. r² = x² + y²

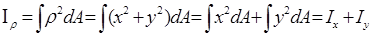
Осевые и полярный моменты инерции всегда положительны и не могут быть = 0. Они измеряются в м⁴ или в см⁴. (1 см⁴ = 10 ^-8 м⁴)

Центробежным моментом инерции относительно некоторых двух взаимно перпендикулярных осей (xy) называют взятую по всей площади сечения А сумму произведений площадей элементарных площадок dA на их расстояния до этих осей.

Центробежный момент может быть положительным, отрицательным и равным нулю в зависимости от положения осей. Измеряется он также в м⁴ или см⁴.

Если какое-либо сечение (плоская фигура) имеет хотя бы одну ось симметрии, то центробежный момент инерции относительно оси симметрии Y и ей перпендикулярной оси X равен нулю. (рис. Трапеции)

Момент инерции сложной фигуры равен сумме моментов инерции её составных частей.

Дата добавления: 2013-12-13