
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Законы геометрической оптики
|
|
|
|
Длины воспринимаемых глазом световых волн очень малы (порядка  м). Поэтому распространение видимого света можно в первом приближении рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых линий, называемых лучами. В предельном случае, соответствующем
м). Поэтому распространение видимого света можно в первом приближении рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых линий, называемых лучами. В предельном случае, соответствующем 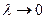 , законы оптики можно сформулировать на языке геометрии. В соответствии с этим раздел оптики, в котором пренебрегают конечностью длин волн, называется геометрической оптикой. Другое название этого раздела - лучевая оптика.
, законы оптики можно сформулировать на языке геометрии. В соответствии с этим раздел оптики, в котором пренебрегают конечностью длин волн, называется геометрической оптикой. Другое название этого раздела - лучевая оптика.
Основу геометрической оптики образуют четыре закона: 1) закон прямолинейного распространения света; 2) закон независимости световых лучей; 3) закон отражения света; 4) закон преломления света.
Закон прямолинейного распространения утверждает, что в однородной среде свет распространяется прямолинейно. Этот закон является приближенным: при прохождении света через очень малые отверстия наблюдаются отклонения от прямолинейности, тем большие, чем меньше отверстие.
Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга. Пересечения лучей не мешают каждому из них распространяться независимо друг от друга. Этот закон справедлив лишь при не слишком больших интенсивностях света. При интенсивностях, достигаемых с помощью лазеров, независимость световых лучей перестает соблюдаться.
Законы отражения и преломления света были сформулированы ранее.
 В основу геометрической оптики может быть положен принцип Ферма: свет распространяется по такому пути, для прохождения которого ему требуется минимальное время.
В основу геометрической оптики может быть положен принцип Ферма: свет распространяется по такому пути, для прохождения которого ему требуется минимальное время.
Для прохождения участка пути 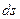 (рис.3.1.2) свету требуется время
(рис.3.1.2) свету требуется время 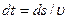 , где
, где  - скорость света в данной точке среды. Заменив
- скорость света в данной точке среды. Заменив  через
через  , получим, что
, получим, что 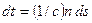 . Следовательно, время
. Следовательно, время 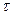 , затрачиваемое светом на прохождение пути от точки 1 до точки 2, равно
, затрачиваемое светом на прохождение пути от точки 1 до точки 2, равно 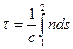 . Имеющая размерность длины величина
. Имеющая размерность длины величина
|
|
|
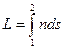
называется оптической длиной пути. В однородной среде оптическая длина пути равна произведению геометрической длины пути 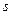 на показатель преломления среды
на показатель преломления среды  :
:  .
.
Отсюда 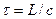 .
.
Пропорциональность времени прохождения 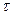 оптической длине пути
оптической длине пути  дает возможность сформулировать принцип Ферма следующим образом: свет распространяется по такому пути, оптическая длина которого минимальна. Точнее, оптическая длина пути должна быть экстремальной, т. е. либо минимальной, либо максимальной, либо стационарной - одинаковой для всех возможных путей. В последнем случае все пути света между двумя точками оказываются таутохронными (требующими для своего прохождения одинакового времени).
дает возможность сформулировать принцип Ферма следующим образом: свет распространяется по такому пути, оптическая длина которого минимальна. Точнее, оптическая длина пути должна быть экстремальной, т. е. либо минимальной, либо максимальной, либо стационарной - одинаковой для всех возможных путей. В последнем случае все пути света между двумя точками оказываются таутохронными (требующими для своего прохождения одинакового времени).
Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален в случае распространения света из точки 1 в точку 2, окажется минимальным и в случае распространения света в обратном направлении. Следовательно, луч, пущенный навстречу лучу, проделавшему путь от точки 1 к точке 2, пойдет по тому же пути, но в обратном направлении. Отставание по фазе 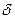 , возникающее на пути с оптической длиной
, возникающее на пути с оптической длиной  , определяется выражением
, определяется выражением

(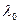 - длина волны в вакууме).
- длина волны в вакууме).
Совокупность лучей образует пучок. Если лучи при своем продолжении пересекаются в одной точке, пучок называется гомоцентрическим. Гомоцентрическому пучку лучей соответствует сферическая волновая поверхность. На рис. 3.1. 3, а) показан сходящийся, а на рис.3.1. 3, б) - расходящийся гомоцентрический пучок. Частным случаем гомоцентрического пучка является пучок параллельных лучей; ему соответствует плоская световая волна.
Всякая оптическая система осуществляет преобразование световых пучков. Если система не нарушает гомоцентричности пучков, то лучи, вышедшие из точки  , пересекутся в одной точке
, пересекутся в одной точке 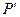 . Эта точка представляет собой оптическое изображение точки
. Эта точка представляет собой оптическое изображение точки  . Если любаяточка предмета изображается в виде точки, изображение называется точечным или стигматическим.
. Если любаяточка предмета изображается в виде точки, изображение называется точечным или стигматическим.
|
|
|
 Изображение называется действительным, если световые лучи в точке
Изображение называется действительным, если световые лучи в точке 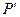 действительно пересекаются (см. рис. 3.1. 3, а), и мнимым, если в
действительно пересекаются (см. рис. 3.1. 3, а), и мнимым, если в 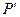 пересекаются продолжения лучей, проведенные в направлении, обратном направлению распространения света (рис. 3.1. 3. б).
пересекаются продолжения лучей, проведенные в направлении, обратном направлению распространения света (рис. 3.1. 3. б).
Вследствие обратимости световых лучей источник света  и изображение
и изображение 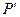 могут поменяться ролями - точечный источник, помещенный в
могут поменяться ролями - точечный источник, помещенный в 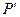 , будет иметь свое изображение в
, будет иметь свое изображение в  . По этой причине
. По этой причине  и
и 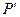 называются сопряженными точками. Оптическая система, которая дает стигматическое изображение, геометрически подобное отображаемому предмету, называется идеальной. С помощью такой системы пространственная непрерывность точек
называются сопряженными точками. Оптическая система, которая дает стигматическое изображение, геометрически подобное отображаемому предмету, называется идеальной. С помощью такой системы пространственная непрерывность точек  отображается в виде пространственной непрерывности точек
отображается в виде пространственной непрерывности точек 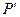 . Первая непрерывность точек называется пространством предметов, вторая — пространством изображений. В обоих пространствах точки, прямые и плоскости однозначно соответствуют друг другу. Такое соотношение двух пространств называется в геометрии коллинеарным соответствием.
. Первая непрерывность точек называется пространством предметов, вторая — пространством изображений. В обоих пространствах точки, прямые и плоскости однозначно соответствуют друг другу. Такое соотношение двух пространств называется в геометрии коллинеарным соответствием.
Оптическая система представляет собой совокупность отражающих и преломляющих поверхностей, отделяющих друг от друга оптически однородные среды. Обычно эти поверхности бывают сферическими или плоскими (плоскость можно рассматривать как сферу бесконечного радиуса).
Оптическая система, образованная сферическими (в частности, плоскими) поверхностями, называется центрированной, если центры всех поверхностей лежат на одной прямой. Эту прямую называют оптической осью системы.
 Каждой точке
Каждой точке  (или плоскости
(или плоскости 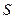 ) в пространстве предметов соответствует сопряженная с ней точка
) в пространстве предметов соответствует сопряженная с ней точка 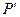 (плоскость
(плоскость 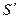 ) в пространстве изображений. Среди бесконечного множества сопряженных точек и сопряженных плоскостей имеются точки и плоскости, обладающие особыми свойствами. Такие точки и плоскости называются кардинальными. К их числу относятся фокальные, главные и узловые точки и плоскости. Задание кардинальных точек или плоскостей полностью определяет свойства идеальной центрированной оптической системы.
) в пространстве изображений. Среди бесконечного множества сопряженных точек и сопряженных плоскостей имеются точки и плоскости, обладающие особыми свойствами. Такие точки и плоскости называются кардинальными. К их числу относятся фокальные, главные и узловые точки и плоскости. Задание кардинальных точек или плоскостей полностью определяет свойства идеальной центрированной оптической системы.
|
|
|
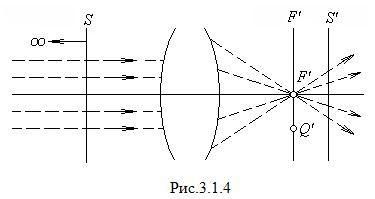
Фокальные плоскости и фокусы оптической системы. На рис. 3.1.4. показаны внешние преломляющие поверхности и оптическая ось некоторой идеальной центрированной оптической системы. Возьмем в пространстве предметов этой системы плоскость 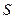 , перпендикулярную к оптической оси. Из соображений симметрии следует, что сопряженная с
, перпендикулярную к оптической оси. Из соображений симметрии следует, что сопряженная с 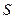 плоскость
плоскость 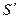 также перпендикулярна к оптической оси. Перемещение плоскости
также перпендикулярна к оптической оси. Перемещение плоскости 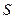 относительно системы вызовет соответствующее перемещение плоскости
относительно системы вызовет соответствующее перемещение плоскости 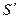 . Когда плоскость
. Когда плоскость 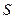 окажется очень далеко, дальнейшее увеличение ее расстояния от системы практически не вызывает изменения положения плоскости
окажется очень далеко, дальнейшее увеличение ее расстояния от системы практически не вызывает изменения положения плоскости 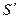 . Это означает,что результате удаления плоскости
. Это означает,что результате удаления плоскости 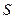 на бесконечность плоскость
на бесконечность плоскость 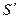 оказывается в определенном предельном положении
оказывается в определенном предельном положении 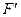 . Плоскость
. Плоскость 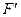 , совпадающая с предельным положением плоскости
, совпадающая с предельным положением плоскости 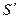 , называется задней фокальной плоскостью оптической системы.
, называется задней фокальной плоскостью оптической системы.
Кратко можно сказать, что задней фокальной плоскостью 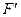 называется плоскость, сопряженная с находящейся на бесконечности в пространстве предметов плоскостью
называется плоскость, сопряженная с находящейся на бесконечности в пространстве предметов плоскостью 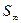 , перпендикулярной к оси системы.
, перпендикулярной к оси системы.
 Точка пересечения задней фокальной плоскости с оптической осью называется задним фокусом системы. Обозначают ее также буквой
Точка пересечения задней фокальной плоскости с оптической осью называется задним фокусом системы. Обозначают ее также буквой 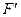 . Эта точка сопряжена с удаленной на бесконечность точкой
. Эта точка сопряжена с удаленной на бесконечность точкой 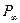 , лежащей на оси системы. Лучи, выходящие из
, лежащей на оси системы. Лучи, выходящие из 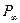 , образуют параллельный оси пучок (рис. 3.1.4). По выходе из системы эти лучи образуют пучок, сходящийся в фокусе
, образуют параллельный оси пучок (рис. 3.1.4). По выходе из системы эти лучи образуют пучок, сходящийся в фокусе 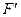 . Упавший на систему параллельный пучок может выйти из системы не в виде сходящегося (как на рис. 3.1.4), а в виде расходящегося пучка. Тогда в точке
. Упавший на систему параллельный пучок может выйти из системы не в виде сходящегося (как на рис. 3.1.4), а в виде расходящегося пучка. Тогда в точке 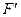 будут пересекаться не сами вышедший лучи, а их продолжения в обратном направлении. Соответственно задняя фокальная плоскость окажется перед (по ходу лучей) системой или внутри системы.
будут пересекаться не сами вышедший лучи, а их продолжения в обратном направлении. Соответственно задняя фокальная плоскость окажется перед (по ходу лучей) системой или внутри системы.
Лучи, вышедшие из бесконечно удаленной точки 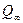 не лежащей на оси системы, образуют параллельный пучок, направленный под углом к оси системы. По выходе из системы эти лучи образуют пучок, сходящийся в точке
не лежащей на оси системы, образуют параллельный пучок, направленный под углом к оси системы. По выходе из системы эти лучи образуют пучок, сходящийся в точке  , принадлежащей задней фокальной плоскости, но не совпадающей с фокусом
, принадлежащей задней фокальной плоскости, но не совпадающей с фокусом 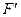 (точка
(точка  на рис. 3.1. 4). Тогда изображение бесконечно удаленного предмета будет лежать в фокальной плоскости.
на рис. 3.1. 4). Тогда изображение бесконечно удаленного предмета будет лежать в фокальной плоскости.
|
|
|
Если удалить на бесконечность перпендикулярную к оси плоскость 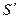 (рис. 3.1. 5), сопряженная с ней плоскость
(рис. 3.1. 5), сопряженная с ней плоскость 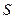 придет в предельное положение
придет в предельное положение 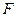 , которое называется передней фокальной плоскостью системы. Кратко можно сказать, что передней фокальной плоскостью
, которое называется передней фокальной плоскостью системы. Кратко можно сказать, что передней фокальной плоскостью 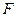 является плоскость, сопряженная с находящейся на бесконечности в пространстве изображений плоскостью
является плоскость, сопряженная с находящейся на бесконечности в пространстве изображений плоскостью  перпендикулярной к оси системы.
перпендикулярной к оси системы.
 Точка пересечения передней фокальной плоскости
Точка пересечения передней фокальной плоскости 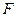 с оптической осью называется передним фокусом системы. Обозначают этот фокус также буквой
с оптической осью называется передним фокусом системы. Обозначают этот фокус также буквой 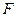 . Лучи, вышедшие из фокуса
. Лучи, вышедшие из фокуса 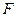 , образуют после выхода из системы пучок параллельных оси лучей. Лучи, вышедшие из точки
, образуют после выхода из системы пучок параллельных оси лучей. Лучи, вышедшие из точки 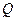 , принадлежащей фокальной плоскости
, принадлежащей фокальной плоскости 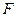 (рис. 3.1. 5), образуют после прохождения через систему параллельный пучок, направленный под углом к оси системы. Может случиться, что параллельный по выходе из системы пучок получается при падении на систему не расходящегося (как на рис. 3.1. 5), а сходящегося пучка лучей. В этом случае передний фокус оказывается за системой или внутри системы.
(рис. 3.1. 5), образуют после прохождения через систему параллельный пучок, направленный под углом к оси системы. Может случиться, что параллельный по выходе из системы пучок получается при падении на систему не расходящегося (как на рис. 3.1. 5), а сходящегося пучка лучей. В этом случае передний фокус оказывается за системой или внутри системы.
Главные плоскости и точки. Рассмотрим две сопряженные плоскости, перпендикулярные к оптической оси системы. Отрезок прямой  (рис. 3.1. 6) лежащий в одной из этих плоскостей, будет иметь своим изображением отрезок прямой
(рис. 3.1. 6) лежащий в одной из этих плоскостей, будет иметь своим изображением отрезок прямой 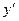 , лежащий в другой плоскости. Из осевой симметрии системы вытекает, что отрезки
, лежащий в другой плоскости. Из осевой симметрии системы вытекает, что отрезки  и
и 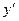 должны лежать в одной, проходящей через оптическую ось, плоскости (в плоскости рисунка). При этом изображение
должны лежать в одной, проходящей через оптическую ось, плоскости (в плоскости рисунка). При этом изображение 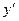 может быть обращено либо в ту же сторону, что и предмет
может быть обращено либо в ту же сторону, что и предмет  (рис.3.1.6, а), либо в противоположную сторону (см. рис. 3.1.6, б). В первом случае изображение называется прямым, во втором - обратным. Отрезки, откладываемые от оптической оси вверх, принято считать положительными, откладываемые вниз – отрицательными.
(рис.3.1.6, а), либо в противоположную сторону (см. рис. 3.1.6, б). В первом случае изображение называется прямым, во втором - обратным. Отрезки, откладываемые от оптической оси вверх, принято считать положительными, откладываемые вниз – отрицательными.
Отношение линейных размеров изображения и предмета называется линейным или поперечным увеличением. Обозначив его буквой  , можно написать
, можно написать
 .
.
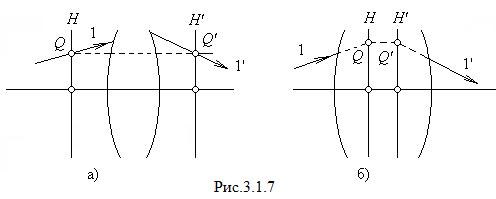 Линейное увеличение - алгебраическая величина. Оно положительно, если изображение прямое (знаки
Линейное увеличение - алгебраическая величина. Оно положительно, если изображение прямое (знаки  и
и 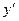 одинаковы), и отрицательно, если изображение обратное (знак
одинаковы), и отрицательно, если изображение обратное (знак 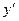 противоположен знаку
противоположен знаку  ).
).
Существуют две такие сопряженные плоскости, которые отображают друг друга с линейным увеличением  . Эти плоскости называются главными. Плоскость, принадлежащая пространству предметов, именуется передней главной плоскостью системы. Ее обозначают буквой
. Эти плоскости называются главными. Плоскость, принадлежащая пространству предметов, именуется передней главной плоскостью системы. Ее обозначают буквой 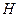 . Плоскость, принадлежащую пространству изображений, именуют задней главной плоскостью. Ее обозначают символом
. Плоскость, принадлежащую пространству изображений, именуют задней главной плоскостью. Ее обозначают символом 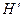 . Точки пересечения главных плоскостей с оптической осью называются главными точками системы (соответственно передней и задней). Их обозначают теми же символами
. Точки пересечения главных плоскостей с оптической осью называются главными точками системы (соответственно передней и задней). Их обозначают теми же символами 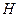 и
и 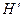 . В зависимости от устройства системы главные плоскости и точки могут находиться как вне, так и внутри системы. Может случиться, что одна из плоскостей проходит вне, а другая - внутри системы. Возможно, наконец, что обе плоскости будут лежать вне системы по одну и ту же сторону от нее.
. В зависимости от устройства системы главные плоскости и точки могут находиться как вне, так и внутри системы. Может случиться, что одна из плоскостей проходит вне, а другая - внутри системы. Возможно, наконец, что обе плоскости будут лежать вне системы по одну и ту же сторону от нее.
 Из определения главных плоскостей вытекает, что луч 1, пересекающий (в действительности – рис. 3.1.7, а или при воображаемом продолжении внутри системы – рис. 3.1. 7, б) переднюю главную плоскость
Из определения главных плоскостей вытекает, что луч 1, пересекающий (в действительности – рис. 3.1.7, а или при воображаемом продолжении внутри системы – рис. 3.1. 7, б) переднюю главную плоскость 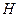 в точке
в точке 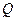 , имеет в качестве сопряженного луч 1', который пересекает (непосредственно или при воображаемом продолжении) главную плоскость
, имеет в качестве сопряженного луч 1', который пересекает (непосредственно или при воображаемом продолжении) главную плоскость 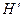 в точке
в точке  , отстоящей в ту же сторону и на такое же расстояние от оси, как и точка
, отстоящей в ту же сторону и на такое же расстояние от оси, как и точка 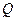 . Это легко понять, если вспомнить, что
. Это легко понять, если вспомнить, что 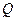 и
и  являются сопряженными точками, и учесть, что любой луч, проходящий через точку
являются сопряженными точками, и учесть, что любой луч, проходящий через точку 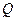 , должен иметь в качестве сопряженного луч, проходящий через точку
, должен иметь в качестве сопряженного луч, проходящий через точку  .
.
 Узловые плоскости и точки. Узловыми точками или узлами называются лежащие на оптической оси сопряженные точки
Узловые плоскости и точки. Узловыми точками или узлами называются лежащие на оптической оси сопряженные точки  и
и  обладающие тем свойством, что проходящие через них (в действительности или при воображаемом продолжении внутрь системы) сопряженные лучи параллельны между собой (см. лучи 1 – 1 ' и 2 – 2' на рис. 3.1. 8). Перпендикулярные к оси плоскости, проходящие через узлы, называются узловыми плоскостями (передней и задней).
обладающие тем свойством, что проходящие через них (в действительности или при воображаемом продолжении внутрь системы) сопряженные лучи параллельны между собой (см. лучи 1 – 1 ' и 2 – 2' на рис. 3.1. 8). Перпендикулярные к оси плоскости, проходящие через узлы, называются узловыми плоскостями (передней и задней).
Расстояние между узлами всегда равно расстоянию между главными точками. В случае, когда оптические свойства сред, находящихся по обе стороны системы, одинаковы (т. е.  ), узлы совпадают с главными точками.
), узлы совпадают с главными точками.
Фокусные расстояния и оптическая сила системы. Расстояние от передней главной точки 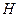 до переднего фокуса
до переднего фокуса 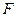 называется передним фокусным расстоянием
называется передним фокусным расстоянием  системы. Расстояние от
системы. Расстояние от 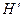 до
до 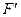 именуется задним фокусным расстоянием
именуется задним фокусным расстоянием 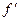 . Фокусные расстояния
. Фокусные расстояния  и
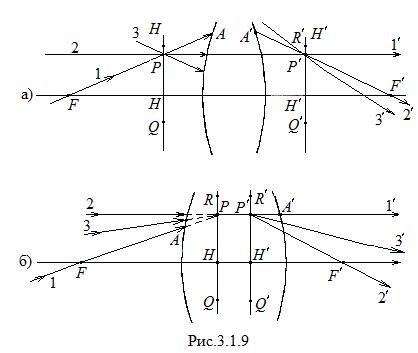
и 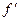 - алгебраические величины. Они положительны, если данный фокус лежит справа от соответствующей главной точки, и отрицательны в противном случае. Например, для системы, изображенной на рис. 3.1.9, заднее фокусное расстояние
- алгебраические величины. Они положительны, если данный фокус лежит справа от соответствующей главной точки, и отрицательны в противном случае. Например, для системы, изображенной на рис. 3.1.9, заднее фокусное расстояние 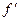 положительно, а переднее фокусное расстояние
положительно, а переднее фокусное расстояние  отрицательно. На рисунке указана истинная длина отрезка
отрицательно. На рисунке указана истинная длина отрезка  , т. е. положительная величина (-
, т. е. положительная величина (- ), равная модулю
), равная модулю  .
.
Можно доказать, что между фокусными расстояниями  и
и 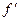 центрированной оптической системы, образованной сферическими преломляющими поверхностями, имеется соотношение
центрированной оптической системы, образованной сферическими преломляющими поверхностями, имеется соотношение
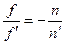 ,
,
где  - показатель преломления среды, находящейся перед оптической системой,
- показатель преломления среды, находящейся перед оптической системой,  - показатель преломления среды, находящейся за системой. Из этого вытекает, что в случае, когда показатели преломления сред, находящихся по обе стороны оптической системы, одинаковы, фокусные расстояния отличаются только знаком:
- показатель преломления среды, находящейся за системой. Из этого вытекает, что в случае, когда показатели преломления сред, находящихся по обе стороны оптической системы, одинаковы, фокусные расстояния отличаются только знаком:
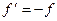 .
.
Величина
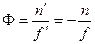
называется оптической силой системы. Чем больше 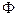 , тем меньше фокусное расстояние
, тем меньше фокусное расстояние 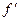 и, следовательно, тем сильнее преломляются лучи оптической системой. Оптическая сила измеряется в диоптриях (дптр). Чтобы получить
и, следовательно, тем сильнее преломляются лучи оптической системой. Оптическая сила измеряется в диоптриях (дптр). Чтобы получить 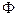 в диоптриях, фокусное расстояние в последней формуле нужно взять в метрах. При положительной
в диоптриях, фокусное расстояние в последней формуле нужно взять в метрах. При положительной 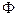 заднее фокусное расстояние
заднее фокусное расстояние 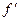 также положительно; следовательно, система дает действительное изображение бесконечно удаленной точки - параллельный пучок лучей превращается в сходящийся. В этом случае система называется собирающей. При отрицательной
также положительно; следовательно, система дает действительное изображение бесконечно удаленной точки - параллельный пучок лучей превращается в сходящийся. В этом случае система называется собирающей. При отрицательной 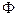 изображение бесконечно удаленной точки будет мнимым - параллельный пучок лучей превращается системой в расходящийся. Такая система именуется рассеивающей.
изображение бесконечно удаленной точки будет мнимым - параллельный пучок лучей превращается системой в расходящийся. Такая система именуется рассеивающей.
Формула системы. Задание кардинальных плоскостей или точек полностью определяет свойства оптической системы. В частности, зная положение кардинальных плоскостей, можно построить оптическое изображение, даваемое системой. Возьмем в пространстве предметов отрезок  , перпендикулярный к оптической оси (рис. 3.1. 10; узлы на рисунке не показаны). Положение этого отрезка можно задать либо расстоянием
, перпендикулярный к оптической оси (рис. 3.1. 10; узлы на рисунке не показаны). Положение этого отрезка можно задать либо расстоянием 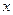 , отсчитанным от точки
, отсчитанным от точки 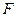 до точки
до точки  , либо расстоянием
, либо расстоянием 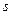 от
от 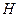 до
до  . Величины
. Величины 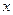 и
и 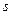 , как и фокусные расстояния
, как и фокусные расстояния  и
и 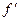 являются алгебраическими (на рисунках указываются их модули).
являются алгебраическими (на рисунках указываются их модули).
Проведем из точки  луч 1, параллельный оптической оси. Он пересечет плоскость
луч 1, параллельный оптической оси. Он пересечет плоскость 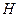 в точке
в точке 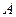 . В соответствии со свойствами главных плоскостей сопряженный лучу 1 луч 1' должен проходить через сопряженную с точкой
. В соответствии со свойствами главных плоскостей сопряженный лучу 1 луч 1' должен проходить через сопряженную с точкой 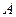 точку
точку 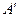 плоскости
плоскости 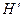 . Так как луч 1 параллелен оптической оси, сопряженный с ним луч 1' пройдет через задний фокус
. Так как луч 1 параллелен оптической оси, сопряженный с ним луч 1' пройдет через задний фокус 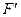 . Теперь проведем из точки
. Теперь проведем из точки  луч 2, проходящий через передний фокус
луч 2, проходящий через передний фокус 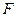 . Он пересечет плоскость
. Он пересечет плоскость 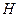 в точке
в точке 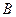 . Сопряженный с ним луч 2' пройдет через сопряженную с
. Сопряженный с ним луч 2' пройдет через сопряженную с 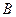 точку
точку  плоскости
плоскости 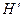 и будет параллельным оптической оси. Точка
и будет параллельным оптической оси. Точка 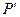 пересечения лучей 1' и 2'представляет собой изображение точки
пересечения лучей 1' и 2'представляет собой изображение точки  . Изображение
. Изображение 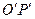 , как и отрезок
, как и отрезок  , перпендикулярно к оптической оси.
, перпендикулярно к оптической оси.

Положение изображения 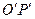 можно охарактеризовать либо расстоянием
можно охарактеризовать либо расстоянием 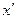 от точки
от точки 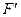 до точки
до точки  , либо расстоянием
, либо расстоянием 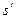 от
от 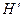 до
до  . Величины
. Величины 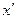 и
и 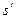 являются алгебраическими. В случае, изображенном на рис. 3.1. 10, они положительны.
являются алгебраическими. В случае, изображенном на рис. 3.1. 10, они положительны.
Величина 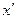 , определяющая положение изображения, закономерно связана с величиной
, определяющая положение изображения, закономерно связана с величиной 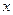 , определяющей положение предмета, и с фокусными расстояниями
, определяющей положение предмета, и с фокусными расстояниями  и
и 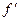 . Для прямоугольных треугольников с общей вершиной в точке
. Для прямоугольных треугольников с общей вершиной в точке 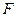 (рис. 3.1. 10) можно написать соотношение
(рис. 3.1. 10) можно написать соотношение
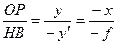 .
.
Аналогично, для треугольников с общей вершиной в точке 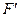 имеем
имеем
 .
.
Объединив оба соотношения, получим что 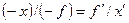 , откуда
, откуда
 . (3.1.4)
. (3.1.4)
Это равенство называется формулой Ньютона. При условии, что  , формула Ньютона имеет вид
, формула Ньютона имеет вид
 . (3.1. 5)
. (3.1. 5)
От формулы, связывающей расстояния 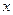 и
и 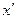 предмета и изображения от фокусов системы, легко перейти к формуле, устанавливающей связь между расстояниями
предмета и изображения от фокусов системы, легко перейти к формуле, устанавливающей связь между расстояниями 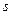 и
и 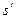 от главных точек. Из рис. 3.1.10 видно, что
от главных точек. Из рис. 3.1.10 видно, что 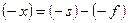 (т. е.
(т. е. 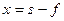 ),
), 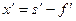 . Подставив эти выражения для
. Подставив эти выражения для 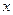 и
и 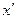 в формулу (3.1.4) и произведя преобразования, получим
в формулу (3.1.4) и произведя преобразования, получим
 . (3.1. 6)
. (3.1. 6)
При выполнении условия 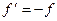 формула (3.1.6) упрощается следующим образом:
формула (3.1.6) упрощается следующим образом:
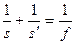 . (3.1.7)
. (3.1.7)
Соотношения (3.1.4) – (3.1.7) представляют собой формулы центрированной оптической системы.
3.1.4.ТОНКАЯ ЛИНЗА
Простейшей центрированной оптической системой является линза. Она представляет собой прозрачное (обычно стеклянное) тело, ограниченное двумя сферическими поверхностями1 (в частном случае одна из поверхностей может быть плоской). Точки пересечения поверхностей с оптической осью линзы называются вершинами преломляющих поверхностей. Расстояние между вершинами именуется толщиной линзы. Если толщиной линзы можно пренебречь по сравнению с меньшим из радиусов кривизны ограничивающих линзу поверхностей, линза называется тонкой.
В случае тонкой линзы главные плоскости 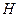 и
и 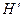 можно считать совпадающими и проходящими через центр линзы
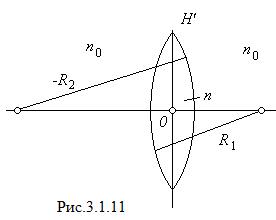
можно считать совпадающими и проходящими через центр линзы  (рис. 3.1.11). Для фокусных расстояний тонкой линзы получается выражение
(рис. 3.1.11). Для фокусных расстояний тонкой линзы получается выражение
 ;
;
здесь  - показатель преломления линзы,
- показатель преломления линзы, 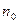 - показатель преломления среды, окружающей линзу,
- показатель преломления среды, окружающей линзу,  и
и  - радиусы кривизны поверхности линзы. С радиусами кривизны нужно обращаться, как с алгебраическими величинами: для выпуклой поверхности (т. е. в случае, когда центр кривизны лежит справа от вершины) радиус кривизны нужно считать положительным, для вогнутой поверхности (т. е. в случае, когда центр кривизны лежит слева от вершины) радиус нужно считать отрицательным. На чертежах указываются модуль радиуса кривизны, т. е.
- радиусы кривизны поверхности линзы. С радиусами кривизны нужно обращаться, как с алгебраическими величинами: для выпуклой поверхности (т. е. в случае, когда центр кривизны лежит справа от вершины) радиус кривизны нужно считать положительным, для вогнутой поверхности (т. е. в случае, когда центр кривизны лежит слева от вершины) радиус нужно считать отрицательным. На чертежах указываются модуль радиуса кривизны, т. е. 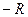 , если
, если 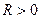 .
.
Если показатели преломления сред, находящихся по обе стороны тонкой линзы, одинаковы, то узлы  и
и  совпадают с главными точками, т. е. помещаются в центре линзы
совпадают с главными точками, т. е. помещаются в центре линзы  . Следовательно, в этом случае любой луч, идущий через центр линзы, не изменяет своего направления. Если показатели преломления сред перед и за линзой неодинаковы, узлы не совпадают с главными точками, так что луч, идущий через центр линзы, претерпевает излом.
. Следовательно, в этом случае любой луч, идущий через центр линзы, не изменяет своего направления. Если показатели преломления сред перед и за линзой неодинаковы, узлы не совпадают с главными точками, так что луч, идущий через центр линзы, претерпевает излом.
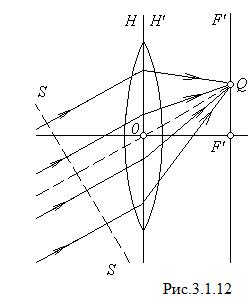 Параллельный пучок лучей после прохождения через линзу собирается в одной из точек фокальной плоскости (точка
Параллельный пучок лучей после прохождения через линзу собирается в одной из точек фокальной плоскости (точка  на рис.3.1. 12). Чтобы определить положение этой точки, нужно продолжить идущий через центр линзы луч до пересечения его с фокальной плоскостью (изображенный пунктиром луч
на рис.3.1. 12). Чтобы определить положение этой точки, нужно продолжить идущий через центр линзы луч до пересечения его с фокальной плоскостью (изображенный пунктиром луч 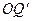 ). В точке пересечения соберутся и остальные лучи. Такой способ пригоден в том случае, если оптические свойства среды по обе стороны линзы одинаковы (
). В точке пересечения соберутся и остальные лучи. Такой способ пригоден в том случае, если оптические свойства среды по обе стороны линзы одинаковы ( ). В противном случае луч, идущий через центр, терпит излом. Для нахождения точки
). В противном случае луч, идущий через центр, терпит излом. Для нахождения точки  в этом случае нужно знать положение узловых точек линзы.
в этом случае нужно знать положение узловых точек линзы.
Отложенные вдоль лучей пути, начинающиеся на волновой поверхности 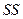 (рис. 3.1. 12) и заканчивающиеся в точке
(рис. 3.1. 12) и заканчивающиеся в точке  , имеют одинаковую оптическую длину и являются таутохронными.
, имеют одинаковую оптическую длину и являются таутохронными.
1 Бывают линзы с поверхностями более сложной формы.
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 589; Нарушение авторских прав?; Мы поможем в написании вашей работы!