Гидравлический расчет просты трубопроводов

ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ.

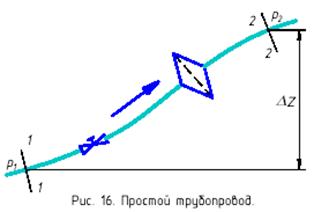Трубопровод без разветвлений принято называть простым. При расчете простых трубопроводов используется физический параметр - потребный напор (иногда этот параметр называют располагаемым напором). Под потребным напором в дальнейшем будем понимать пьезометрический напор в начальном сечении, обеспечивающий заданный расход жидкости в данном трубопроводе.

На рис.16 изображен про­стой трубопровод постоянного се­чения диаметром d и длиной l с несколькими местными сопротивлениями. Если записать уравнение Бернулли для сечений 1-1 и 2-2, то после математических преобразований получим выражение для потребного напора

, (30)

где - перепад высот между конечным и начальным сечениями;

- давление в конечном сечении;

- суммарные потери от сечения 1-1 до 2-2.

Суммарные потери напора в общем случае можно представить в виде

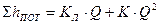. (31)

B правой части зависимости (31) суммированы потери напора в гидравлических сопротивлениях, которые имеют место в данном трубопроводе. Первое слагаемое присутствует при наличии ламинарных потерь на трение по длине или линейных потерь в местных сопротивлениях. Второе - при наличии турбулентных потерь на трение по длине или квадратичных потерь в местных сопротивлениях.

Коэффициент может быть получен из формулы Пуазейля (22) с учетом положений раздела 5.3.2, а коэффициент K - из формул Дарси (19) и Вейсбаха (18) с учетом зависимости для расхода (14). Эти коэффициенты определяются геомет­рическими параметрами трубопроводов и свойствами жидкости. Следует однако отметить, что при турбулентном течении (особенно в области гидравлически гладких труб) коэффициент К может несколько зависеть от расхода (см. раздел 5.2).

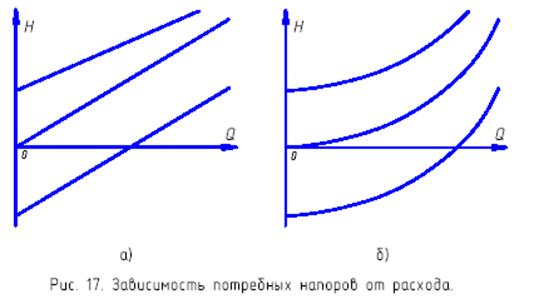
Кривые потребного напора приведены на рис.17. Причем, на рис.17а зависимости носят линейный характер, т.е. , а на рис.17б - квадратичный.

Зависимости потребных напоров связывают основные геометрические параметры трубопроводов, характеристики жидкости и параметры потока. Они могут быть представлены в графическом (рис.17) или в аналитическом (30), (31) виде. Эти зависимости позволяют существенно упростить расчеты сложных гидравлических систем.

B ряде случаев вместо зависимостей потребного напора используют характеристики трубопроводов. Характеристика трубопровода это зависимость суммарных потерь от расхода, т.е. . Она отличается от линии потребного напора на величину так называемого статического напора

(32)

и применяется в расчетах машиностроительных объемных гидросистем.

Дата добавления: 2013-12-14