Конспект излагаемого материала

В макроэкономике модели разрабатываются для объяснения причин происходящих явлений и для прогноза их дальнейшего развития. Прогноз этот учитывается при принятии управленческих решений, но сами модели обычно не дают рекомендаций по этим решениям Объяснения причин часто остаются тенденциозными и при использовании математических моделей.

В микроэкономике к указанным выше целям добавляется задача о справедливом распределении выгод от совместной деятельности экономических субъектов или ущерба от совместного загрязнения окружающей среды, а также задача выбора оптимальной стратегии в условиях конфликта.

В экономике предприятия математические модели используются для учета и прогноза, для оптимального распределения ресурсов по подразделениям предприятия и по достигаемым целям. Мы рассмотрим простейшие модели управления запасами.

Если на рынках государства или региона за год или квартал реализуется товаров на сумму Q в ценах базового периода, уровень цен составляет Р по отношению к базовому периоду, а скорость обращения денег (среднее количество участий имеющегося в обращении денежного средства в опера­циях купли-продажи за тот период, когда реализуются товары на сумму Q) равна V, то для нормальной работы рынка нужно, чтобы масса находящихся в обращении денег М определялась формулой

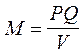. (1)

Формулу (1) называют законом Ирвинга Фишера в часть того Фишера, который первым ее обосновал и опубликовал. При хорошо работающей банковской системе формула (1) должна выполняться автоматически, но это бывает редко: часто для этого нужны энергичные (и иногда непопулярные) меры со стороны государства.

Если денег не хватает, , то оплатить все сделки в срок невозможно. Растет бартер, происходит задержка платежей и снижение цен на некоторые товары, что ведет к спаду их производства и уменьшению Q. Уменьшение Q означает снижение жизненного уровня и рост безработицы, но оно восстанавливает равенство (1), так что это равенство устойчиво по отношению к нехватке денег, хотя последствия этой нехватки весьма неприятны.

Если денег по какой-то причине оказалось слишком много, 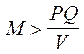, то начинается инфляция с ростом спроса, ростом уровня цен Р и производства, что вызывает рост Q. Но без специальных мер по ограничению спроса рост Р влечет за собой гораздо более быстрый рост V, так как физичес­кие и юридические лица, желающие спасти свои деньги от инфляции, стремятся побыстрее обменять их на нужные товары. В итоге не растет, а убывает и инфляция сама себя усиливает: равенство (1) неустойчиво по отношению к избытку денег.

Инфляция может начаться без избытка денег из-за роста цен, связанного с ростом себестоимости товаров, торговых издержек или косвенных налогов, а уже затем рост V приводит к избытку денег, иногда даже без увеличения их количества.

Как правило, спрос y на товар зависит от его цены x, убывает с ростом x и растет при уменьшении. Величина

E_x(y) = 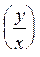(2)

называется эластичностью спроса по цене. Спрос называется эластичным, если ½ E_x(y) ½>1, и неэластичным при ½ E_x(y) ½<1. Если известна формула, выражающая зависимость спроса от цены, то вместо берут . Но обычно эта формула неизвестна и есть только два значения цены х₁ и х₂ и спрос при этих ценах y₁ и y₂. Тогда Dy=y₁–y₂, Dx=x₁–x₂, а в качестве берут , если нужна эластичность при цене х₁, или , если нужна средняя эластичность спроса на отрезке x₁£x£x₂.

Модели управления запасами в торговле и промышленности используются часто. Простейшая из них – детерминированная однопродуктовая модель управления текущими запасами. Такой запас расходуется приблизительно равномерно со скоростью b единиц в день, пополняется партиями по q единиц, так что одной партии хватает на дней. Затраты на хранение товара пропорциональны его среднему количеству и времени хранения, а так как среднее количество хранимого товара 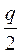, они равны , где с₁ – затраты на хранение единицы товара в день.

Расход на закупку партии товара составляет aq+c₀, где a – цена единицы товара с учетом части затрат на его доставку, пропорциональной q, а с₀ – разовые расходы на оформление заказа и доставку, не зависящие от величины q. Общие затраты R на хранение и пополнение текущих запасов товара выражаются формулой

(3)

Так как обычно с₀ и а выражены в рублях, а с₁ – в копейках на единицу товара в день, то для счета по формуле (3) и выводимым из нее формулам (4) и (5), надо перевести с₁ в рубли (или с₀ и а в копейки). Экономиста обычно интересует не величина R, а расходы на обеспечение товаром в день. Из формулы (3) и равенства получаем

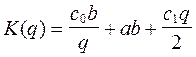(4)

Величина закупаемой партии q обычно определяется руководством предприятия, которое создает и использует текущий запас товара. Если надо уменьшить затраты K(q), то оптимальным считают то из допустимых значений q, которое обеспечивает минимум K(q). Для нахождения этого q обозначают его через x и записывают

K(х)= c₀bx^-1+ab+0.5c₁x,

затем приравнивают нулю производную K'(x) и получают уравнение

K'(x)=с₀bx^-2=0.5с₁=0,

откуда, с учетом очевидного неравенства x>0,

. (5)

Найденное x не всегда является допустимым значением q: предприя­тия закупают товар оптом и q должно содержать целое число упаковок товара и быть не меньше минимальной партии q_min, установленной поставщиком. Если x по формуле (5) меньше q_min, то q = q_min, иначе округляют x до ближайшей величины, кратной количеству h товара в упаковке.

Заказанный товар обычно поступает не сразу, а через некоторое время t после начала оформления заказа. Если время t неизвестно заранее, то мо­жно подсчитать, при количестве Q товара на складе надо начинать оформлять заказ на пополнение запаса. Величина Q называется точкой заказа и при t<T определяется равенством

Q = bt, (6)

которое означает, что имеющегося на складе товара хватит как раз до поступления новой партии. Если t>T, но t<2T, то

Q = b(t–T)=bt–q, (7)

так как в этом случае на момент заказа одна ранее заказанная партия из q единиц находится в пути к заказчику. Можно записать формулы, аналогичные (7) при t>2T, но такие случаи встречаются редко.

В условиях рыночной экономики почти каждый товар можно приобрести у разных поставщиков, у каждого из которых свои условия поставки, свои значения a, c₀ и q_min. Обычно поставщика выбирают в зависимости от надежности поставок и качества поставляемого товара, но если товар у поставщиков одинаков и все они надежные, то можно выбрать исходя из условия минимума величины K(q_min). Для каждого из подходящих поставщиков вычисляют x по формуле (5), находят q по вычисленному x, а затем вычисляют K(q) по формуле (4): лучше тот поставщик, у которого K(q) минимальна.

Задача управления запасами при случайном спросе ставится в терминах теории вероятностей: величина закупаемой партии должна обеспечивать максимум математического ожидания прибыли или минимум математического ожидания ущерба от возможной нехватки и возможного избытка товара. Для решения этой задачи надо знать закон распределения спроса a:

F(x)=P( a< x).

Обычно методами математической статистики находят по прошлому опыту функцию P(x) – плотность распределения спроса, если спрос непрерывен, или таблицу возможных значений x_k спроса и их вероятностей P_k, если спрос дискретен. При непрерывном распределении спроса

, (8)

так как спрос a не бывает меньше нуля, а в дискретном случае

. (9)

Зная F(x), экономист может выбрать оптимальные параметры управления, например, оптимальный размер закупаемой партии или сроки закупки, обеспечивающие минимум математического ожидания суммы ущерба от нехватки товара и ущерба от его избытка.

Если ущерб от нехватки одной единицы товара у_нехв, а ущерб от избытка у_изб, то при непрерывном распределении спроса оптимальный размер х_опт закупаемой партии этого товара определяется из уравнения

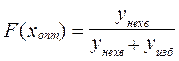(10)

Если товар штучный, величина спроса всегда является целым числом и вместо равенства (10) получим два неравенства

(11)

Математическую модель конфликта или сотрудничества называют игровой моделью, или просто игрой. Это связано с тем. что первые модели этого типа были построены для изучения азартных игр. Физическое или юридическое лицо или команда, участвующая в конфликте или сотрудничестве, называется игроком, а вектор-функция, координаты которой суть прибыли игроков, – функцией выигрыша. Иногда рассматривают только координату вектора, относящуюся к i- му игроку, и называют ее функцией выигрыша этого игрока.

Принято считать, что игрок хочет увеличить свою функцию выигрыша и что ему безразлично, как при этом меняются функции выигрыша других игроков. Игроки могут объединяться в коалиции для совместных действий. При вступлении в коалицию цель игрока не меняется, но меняется способ достижения этой цели.

Из научных дисциплин, изучающих игровые модели, с экономикой связаны классическая теория игр, теория активных систем и теория рефлексивного управления. В классической теории игр принимают за аксиомы, что игроки равноправны и что каждый из них считает другого игрока умным (не глупее себя) и осторожным. Отказ от первой из этих аксиом приводит к теории активных систем, а от второй – к теории рефлексивного управления. В этой теории считается, что один из игроков, более умный, составляет модель поведения другого и может либо надежно предсказать его действия, либо даже путем передачи определенной информации, правдивой или ложной, управлять этими действиями, хотя второй игрок уверен, что действует по своей воле.

Полезность u(q) денег или другого товара для игрока зависит от количества q этого товара и возрастает с ростом q, так что u'(q)>0. Если товар штучный, то математики продолжают заданную при целых значениях q функцию u на вещественные значения так, что она становится непрерывной вместе с первыми двумя производными. Величина u'(q) называется фиктивной ценой товара и обычно убывает с ростом q, так что u''(q)<0. Функции полезности используются в разных экономических задачах, в том числе в описанной ниже задаче о сделках.

Простейшими моделями классической теории игр являются игра двух лиц с противоположными интересами (антагонистическая игра) и модель коалиции из двух или нескольких игроков. Главная проблема, возникающая при создании коалиции, – проблема распределения выгоды от сотрудничества.

Пусть игроки, входящие в коалицию, имеют функции полезности u₁(q₁), u₂(q₂),.., u_i(q_i), где q_i – количество товара у i -го игрока. Если без вступления в коалицию i -й игрок будет иметь q_i^* товара, а в коалиции получит q_i>q_i^* (без условия q_i>q_i^* он не войдет в коалицию), то согласно теории американского математика Джона Нэша справедливым распределением выгоды от сотрудничества следует считать такое, при котором достигается максимум произведения

.

Например, если n=2, игрок A имеет капитал a и функцию полезности lnq₁, а игрок B – капитал b и функцию полезности 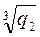, а в результате сделки они получат прибыль с, которую могут разделить, отдав х игроку А и с–х игроку B, то решением задачи о сделках будет величина x на отрезке 0<x<c, при которой достигается

. (12)

Задачи типа (12) решаются обычно на ЭВМ с использованием имеющегося готового программного обеспечения.

Еще одна простая игровая модель, рассматриваемая в классической теории игр, – модель открытых торгов (аукциона) или закрытых торгов (конкурса) за два лота, в которых реальных покупателей тоже два: A и B, а имеющиеся у них для покупки лотов суммы S_A и S_B примерно равны. Пусть ценность первого лота для игрока А равна V₁, второго V₂ и V₁ + V₂ < S_A, т.е. А непрочь купить оба лота и готов отдать за них S_A. Пусть B находится в аналогичном положении, но его оценки лотов W₁ и W₂ неизвестны А, и ему неизвестны V₁ и V₂.

Если А купит первый лот за х, он вынужден будет прекратить торг за второй лот при цене S_A–х и уступить за эту цену второй лот B. Доход A составит при этом V₁–x; эта разность убывает с ростом х. Если В купит первый лот за х, то А сможет купить второй за S_A–х и доход А составит

V₂–(S_B-x)=V₂+x–S_B.

Эта разность растет с ростом x и при

(13)

равна V₁–х. Поэтому при цене за первый лот меньше х_пор игроку А выгоднее продолжать торг, а при цене больше х_пор выгоднее уступить этот лот, чтобы купить второй.

Величины W₁ и W₂ обычно не равны V₁ и V₂, S_A и S_B тоже часто немного отличаются друг от друга, поэтому на практике один из игроков – А или В – прекращает торг за первый лот раньше другого.

Сложнее обстоит дело при закрытых торгах, когда окончательную цену надо назначить сразу. В этом случае игроку очень полезно знать, как оценивает лоты его конкурент: это знание позволит ему использовать модели рефлексивного управления и увеличить свой доход.

Домашняя работа №1 (Управление запасами)

Величина n равна номеру по журналу учета учебных занятий.

Дата добавления: 2013-12-14