Рівняння Лапласа в циліндричних координатах

Мішана задача

Задача Неймана

Задача Діріхле

Ця задача (перша крайова задача) у просторі формулюється так: знайти функцію 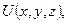яка задовольняє всередині замкненої поверхні 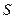рівняння Лапласа 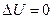та набуває у кожній точці М поверхні 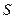заданих значень:

К.У.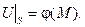 (6.37)

Очевидним можна вважати той факт, що задача Діріхле завжди має розв’язок. Дійсно, якщо, наприклад, кожна точка на поверхні тіла постійно підтримується при певній заданій температурі (яка може бути різною у різних точках поверхні), то у кожній точці тіла встановиться своя температура, яка і дає розв’язок задачі Діріхле при заданих крайових умовах. Також очевидно, що цей розв’язок буде єдиним.

Аналогічно формулюється задача Діріхле у двовимірному випадку: знайти функцію 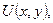яка задовольняє всередині замкненої кривої Г рівняння Лапласа та набуває у кожній точці М кривої Г заданих значень:

К.У.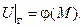 (6.38)

Зазначимо, що задача Діріхле розв’язується дуже просто в одновимірному випадку, коли розглядається, наприклад, стаціонарний розподіл температури у тонкому стержні довжини l з теплоізольованою бічною поверхнею. Тоді задача Діріхле ставиться так: знайти функцію яка задовольняє рівняння Лапласа для усіх і набуває на кінцях стержня заданих значень:

К.У.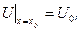 (6.39)

Задача Діріхле у цьому випадку має розв’язок

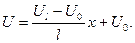(6.40)

задача Неймана (друга крайова задача)формулюється так: знайти функцію 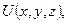яка задовольняє всередині замкненої поверхні 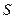рівняння Лапласа та її похідна по напрямку зовнішньої нормалі у кожній точці М поверхні 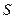набуває заданих значень:

К.У. (6.41)

Нагадуємо, що похідна пов’язана з потоком тепла через поверхню 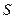. Аналогічно формулюється задача Неймана для двовимірного та одновимірного випадків.

Мішана задача (третя крайова задача) формулюється так: знайти функцію яка задовольняє всередині замкненої поверхні 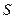рівняння Лапласа, а у кожній точці М поверхні 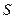виконується умова:

К.У. (6.42)

де функції та є заданими. Цю задачу ще називають задачею з косою похідною.

Нехай – гармонічна в деякій області 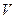функція трьох змінних. Тоді для неї рівняння Лапласа має вигляд:

(6.43)

Введемо у розгляд циліндричні координати які пов’язані з декартовими координатами формулами

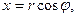
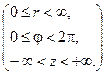, (6.44)

Звідси зворотній зв’язок:

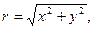
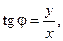
(6.45)

Щоб записати рівняння Лапласа в циліндричних координатах, знайдемо відповідні частинні похідні функції , використовуючи формули диференціювання складеної функції декількох змінних:

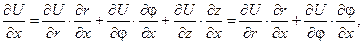
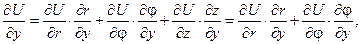
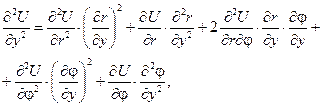
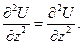
Враховуючи, що:

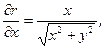
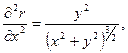
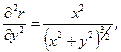
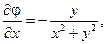
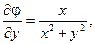
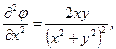
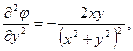
отримаємо:

(6.46)

Це і є рівняння Лапласа в циліндричних координатах.

Якщо функція U не залежить від z, а лише від x та y, то рівняння Лапласа буде мати вигляд

(6.47)

де r та – полярні координати на площині. Знайдене рівняння є рівнянням Лапласа в полярних координатах.

Приклад 6.3 Знайдемо розв’язок рівняння Лапласа в області D, що обмежена двома колами та 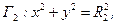якщо значення шуканої функції на колах:

К.У.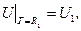

де та – сталі.

Це може бути, наприклад, задача про стаціонарний розподіл температури у кільці між двома колами, якщо на самих колах температура задана.

Розв’язуємо задачу у полярних координатах. Очевидно, шукана функція 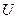не залежить від кута . Тоді рівняння Лапласа набуває простішого вигляду:

Це звичайне диференціальне рівняння другого порядку, яке допускає пониження порядку. Інтегруючи його, знайдемо

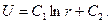
Визначимо та із крайових умов:

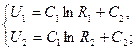
звідси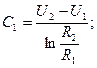

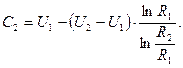
остаточно отримаємо:

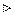
Дата добавления: 2013-12-14